Floyd判圈算法(Floyd Cycle Detection Algorithm)，又称龟兔赛跑算法(Tortoise and Hare Algorithm)，是一个可以在有限状态机、迭代函数或者链表上判断是否存在环，求出该环的起点与长度的算法。

判环

我们定义两个指针，一快一慢，慢指针每次走一步，快指针每次走两步；当两个指针从链表的同一节点开始移动时，若链表中无环，则快指针一直在慢指针前；否则，快指针会先于慢指针入环，且会在慢指针跑满环中一圈之前，追上快指针！。

slow=head,fast=head;
while(fast!=nullptr){
    if(fast->next==nullptr)
        return false;
       fast=fast->next->next;
    slow=slow->next;
    if(fast==slow)
        return true;
}
return false;

求环的起点与长度

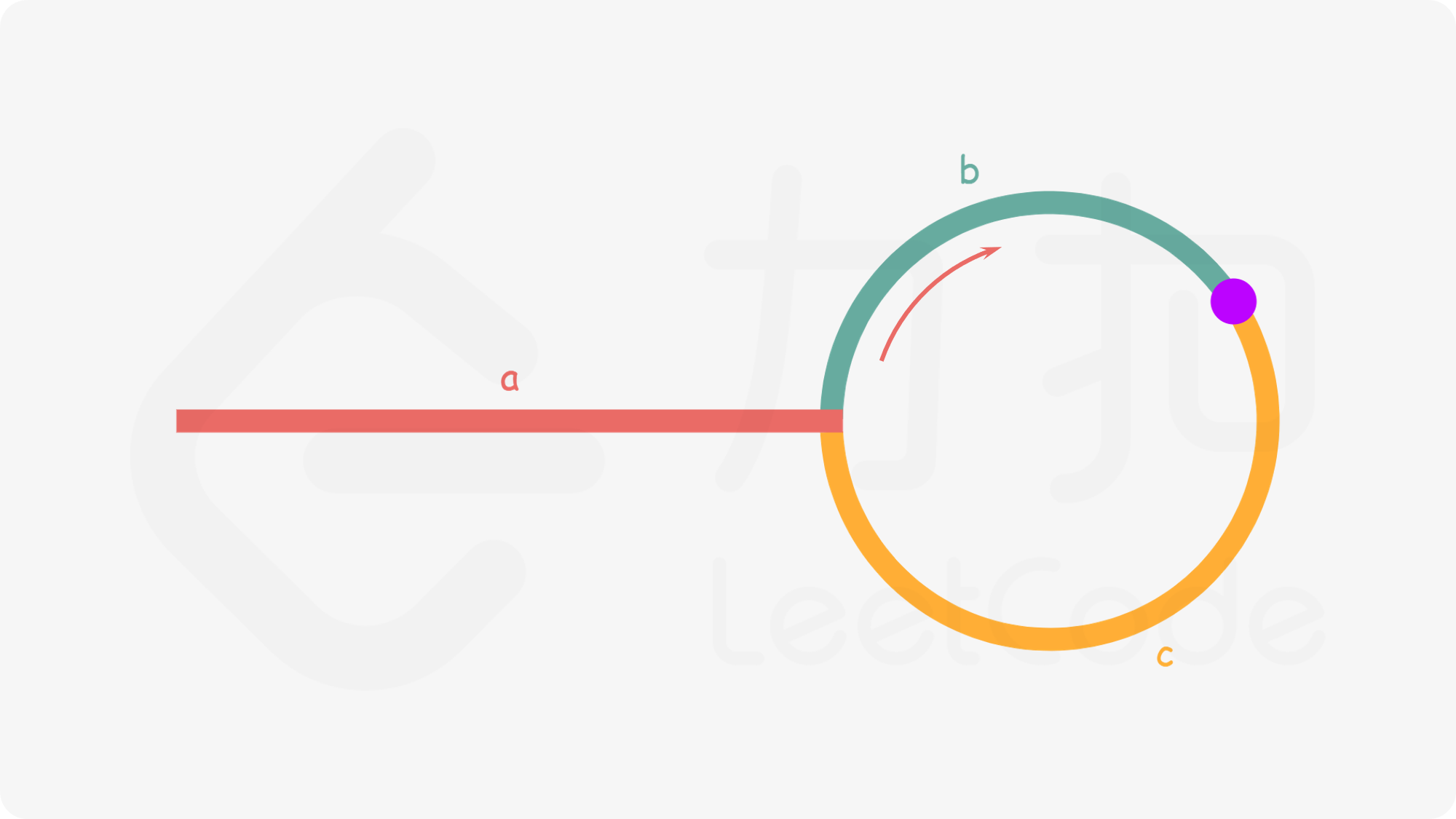
基于Floyd判圈算法， 设置快慢指针fast和slow，假设fast和slow在P点相遇，且fast已跑n圈，可得出如下结论

联立后，可得出
即环外距离等于【相遇点与环起点距离c】和【多圈环长度】之和
故当快慢指针相遇时，设置新ptr指针指向头结点。并令ptr和slow指针同步运动，直到两指针相遇时，便为环的起点。

{
    auto slow=head,fast=head;
    while(fast!=nullptr){
        if(fast->next==nullptr)
            return nullptr;
        fast=fast->next->next;
        slow=slow->next;
        if(fast==slow){
            auto ptr=head;
            while(ptr!=slow){
                slow=slow->next;
                ptr=ptr->next;
            }
            return ptr;
        }
    }
    return nullptr;
 }