https://leetcode-cn.com/problems/path-with-minimum-effort/solution/dfs-er-fen-cha-zhao-mo-ban-ti-by-kobe24o/

  • 「使……最大值尽可能小」是二分搜索题目常见的问法。
  • 「将数组分割为 m 段，求……」是动态规划题目常见的问法。

☆☆☆1631. 最小体力消耗路径

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。 示例 1：

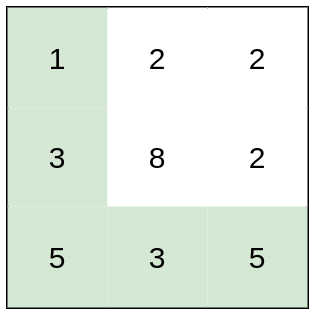
输入：heights = [[1,2,2],[3,8,2],[5,3,5]] 输出：2 解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。 这条路径比路径 [1,2,2,2,5] 更优，因为另一条路劲差值最大值为 3 。

image.png

二分法+dfs

思路

「使……最大值尽可能小」是二分搜索题目常见的问法。
本题中，我们注意到当选取一个mid时，若矩阵中存在一条路径的体力<=mid时，便设置右边界为mid-1，保存mid；若不存在，则说明矩阵中不存在任何一条路径存在该值，故设置左边界为mid+1;
对于矩阵搜索中是否存在一条路径满足mid，可采用DFS，对于某点(i,j)，在其满足条件的方向上，若不存在体力值＜mid,则返回
；若存在一条，且最终该点可以走到(m-1,n-1)，则返回true;

算法

本题的难度在与如何剪枝，方法如下：

  • 每次二分查找维护一个二维数组vis，保证所有探索过的路径不会经过第二次。

  • 若在探索途中发现体力值>mid，则无须继续探索该方向，选取下一个方向（因为只要找到一条路径即可）

    实现

    1. class Solution {
    2.   vector<vector<int>> dir={{0,1},{0,-1},{1,0},{-1,0}};
    3.   int m,n;
    4. public:
    5.   int minimumEffortPath(vector<vector<int>>& heights) {
    6.       m=heights.size();
    7.       n=heights[0].size();
    8.       int l=0,r=1e6,ans=0;
    9.       while(l<=r){
    10.           int mid=l+((r-l)>>1);
    11.           vector<vector<bool>> vis(m,vector<bool>(n,false));
    12.           if(dfs(heights,vis,0,0,mid)){
    13.               // if x existed,x<=mid。
    14.               r=mid-1;
    15.               ans=mid;
    16.           }
    17.           else{
    18.               //all x >mid
    19.               l=mid+1;
    20.           }
    21.       }
    22.       return ans;
    23.   }
    24.   bool dfs(vector<vector<int>>& heights,vector<vector<bool>>& vis,int x,int y,int tar){
    25.       if(x==m-1 && y==n-1){
    26.           return true;
    27.       }
    28.       vis[x][y]=true;
    29.       int i,j,k;
    30.       for(k=0;k<4;k++){
    31.           int i=x+dir[k][0];
    32.           int j=y+dir[k][1];
    33.           if(i>=0 && i<m && j>=0 && j<n
    34.               && !vis[i][j]
    35.               && abs(heights[i][j]-heights[x][y])<=tar){
    36.                   if(dfs(heights,vis,i,j,tar)){
    37.                       return true;
    38.                   }
    39.           }
    41.       }
    42.       return false;
    43.   }
    44. };

    复杂度分析

  • 时间复杂度:☆☆☆模板集群：极大极小化 - 图2

  • 空间复杂度:☆☆☆模板集群：极大极小化 - 图3，vis所占用的空间。

☆☆☆410. 分割数组的最大值

给定一个非负整数数组和一个整数 m，你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。

注意: 数组长度 n 满足以下条件:

  1. 1 ≤ n ≤ 1000
  2. 1 ≤ m ≤ min(50, n)

示例:

输入:

nums = [7,2,5,10,8]

m = 2

输出:

18

解释:

一共有四种方法将nums分割为2个子数组。

其中最好的方式是将其分为[7,2,5] 和 [10,8]，

因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

贪心+二分法

思路

「使……最大值尽可能小」是二分搜索题目常见的问法。

本题中，我们注意到：当我们选定一个值 mid，我们可以线性地验证是否存在一种分割方案，满足其最大分割子数组和不超过mid。策略如下：
针对mid,遍历数组，最大化每个子数组内元素的个数，保证sum(subArray)<=x;

  • 若最大化子数组个数cnt<=m，说明依靠mid来分组，组数可能不满足，需要减少mid，故令右边界为mid

  • 若cnt>m,说明组数过多，mid小了，故左边界为mid；

    算法

  • 设置左右边界： l=max(nums);r=sum(nums)

  • 设置二分条件

    实现

    1. class Solution {
    2. public:
    3.   int splitArray(vector<int>& nums, int m) {
    4.       int l=0,r=0,ans=0;
    5.       for(auto val:nums){
    6.           if(l<val) l=val;
    7.           r+=val;
    8.       }
    9.       return binary(nums,m,l,r);
    10.   }
    11.   int binary(vector<int>& nums,int m,int l,int r){
    12.       int n=nums.size();
    13.       while(l<r){
    14.           int mid=l+((r-l)>>1);
    15.           int curSum=0,cnt=1;
    16.           for(int i=0;i<n;i++){
    17.               curSum+=nums[i];
    18.               if(curSum>mid){
    19.                   cnt++;
    20.                   curSum=nums[i];
    21.               }
    22.           }
    23.           if(cnt<=m){
    24.               r=mid;
    25.           }
    26.           else{
    27.               l=mid+1;
    28.           }
    29.       }
    30.       return l;
    31.   }
    32. };

    复杂度分析

  • 时间复杂度:☆☆☆模板集群：极大极小化 - 图4

  • 空间复杂度:☆☆☆模板集群：极大极小化 - 图5

    动态规划

    思路

    「将数组分割为 m 段，求……」是动态规划题目常见的问法。
    设置f[i][j]为前i个数分割为j段的和的最大值的最小值。现在考虑状态转移方式：
    对于f[i][j],考虑j-1段的问题,其为前k个元素，则f[i][``j]的值就取决于f[k][j-1]与sub(k,i),其中sub(k,i)为第j段的和，故状态转移方程如下：
    ☆☆☆模板集群：极大极小化 - 图6
    由于不能分出空的数组，限制条件为☆☆☆模板集群：极大极小化 - 图7,对于i<j的情况，由于要求出最小值，故将其设为一个很大的值。
    ☆☆☆模板集群：极大极小化 - 图8

    算法

  • 求解状态转移方程

  • 对状态转移方程进行分析

  • 设置初值。

    实现

    1. class Solution {
    2. public:
    3.   int splitArray(vector<int>& nums, int m) {
    4.       int n=nums.size();
    5.       vector<vector<long long>> dp(n+1,vector<long long>(m+1,INT_MAX));
    6.       dp[0][0]=0;
    7.       vector<long long> segSum(n+1,0);
    8.       for(int i=0;i<n;i++){
    9.           segSum[i+1]=segSum[i]+nums[i];
    10.       }
    11.       for(int i=1;i<n+1;i++){
    12.           //i>=j
    13.           for(int j=1;j<=min(i,m);j++){
    14.               //k>=j-1
    15.               for(int k=j-1;k<i;k++){
    16.                   dp[i][j]=min(dp[i][j],max(dp[k][j-1],segSum[i]-segSum[k]));
    17.               }
    18.           }
    19.       }
    20.       return dp[n][m];
    21.   }
    22. };

    复杂度分析

  • 时间复杂度:☆☆☆模板集群：极大极小化 - 图9

  • 空间复杂度:☆☆☆模板集群：极大极小化 - 图10

题目标题难度划分

星级 题目难度
☆ 简单
☆☆ 中等
☆☆☆ 困难

算法掌握难度程度划分

星级 掌握难度
无 普通
❤ 经典，易掌握
❤❤ 经典，略难掌握
❤❤❤ 困难