确定有限状态自动机(以下简称「自动机」)是一类计算模型。它包含一系列状态,这些状态中:
有一个特殊的状态,被称作「初始状态」。 还有一系列状态被称为「接受状态」,它们组成了一个特殊的集合。其中,一个状态可能既是「初始状态」,也是「接受状态」。
起初,这个自动机处于「初始状态」。随后,它顺序地读取字符串中的每一个字符,并根据当前状态和读入的字符,按照某个事先约定好的「转移规则」,从当前状态转移到下一个状态;当状态转移完成后,它就读取下一个字符。当字符串全部读取完毕后,如果自动机处于某个「接受状态」,则判定该字符串「被接受」;否则,判定该字符串「被拒绝」。
注意:如果输入的过程中某一步转移失败了,即不存在对应的「转移规则」,此时计算将提前中止。在这种情况下我们也判定该字符串「被拒绝」。
一个自动机,总能够回答某种形式的「对于给定的输入字符串 S,判断其是否满足条件 P」的问题。在本题中,条件 P 即为「构成合法的表示数值的字符串」。
自动机驱动的编程,可以被看做一种暴力枚举方法的延伸:它穷尽了在任何一种情况下,对应任何的输入,需要做的事情。
☆☆剑指 Offer 20. 表示数值的字符串
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串”+100”、”5e2”、”-123”、”3.1416”、”-1E-16”、”0123”都表示数值,但”12e”、”1a3.14”、”1.2.3”、”+-5”及”12e+5.4”都不是。
问题描述——何为合法的数值字符串?
在 C++ 文档 中,描述了一个合法的数值字符串应当具有的格式。具体而言,它包含以下部分:
- 符号位,即 +++、−-− 两种符号- 整数部分,即由若干字符 0−90-90−9 组成的字符串- 小数点- 小数部分,其构成与整数部分相同- 指数部分,其中包含开头的字符 e大写小写均可)、可选的符号位,和整数部分
相比于 C++ 文档而言,本题还有一点额外的不同,即允许字符串首末两端有一些额外的空格。
思路
1. 自动机「状态集合」
根据如上描述,采用常用技巧:用「当前处理到字符串的哪个部分」当作状态的表述。根据这一技巧,不难挖掘出所有状态:
- 起始的空格
- 符号位
- 整数部分
- 左侧有整数的小数点
- 左侧无整数的小数点(根据前面的第二条额外规则,需要对左侧有无整数的两种小数点做区分)
- 小数部分
- 字符 e
- 指数部分的符号位
- 指数部分的整数部分
- 末尾的空格
2.「初始状态」与「接受状态集合」
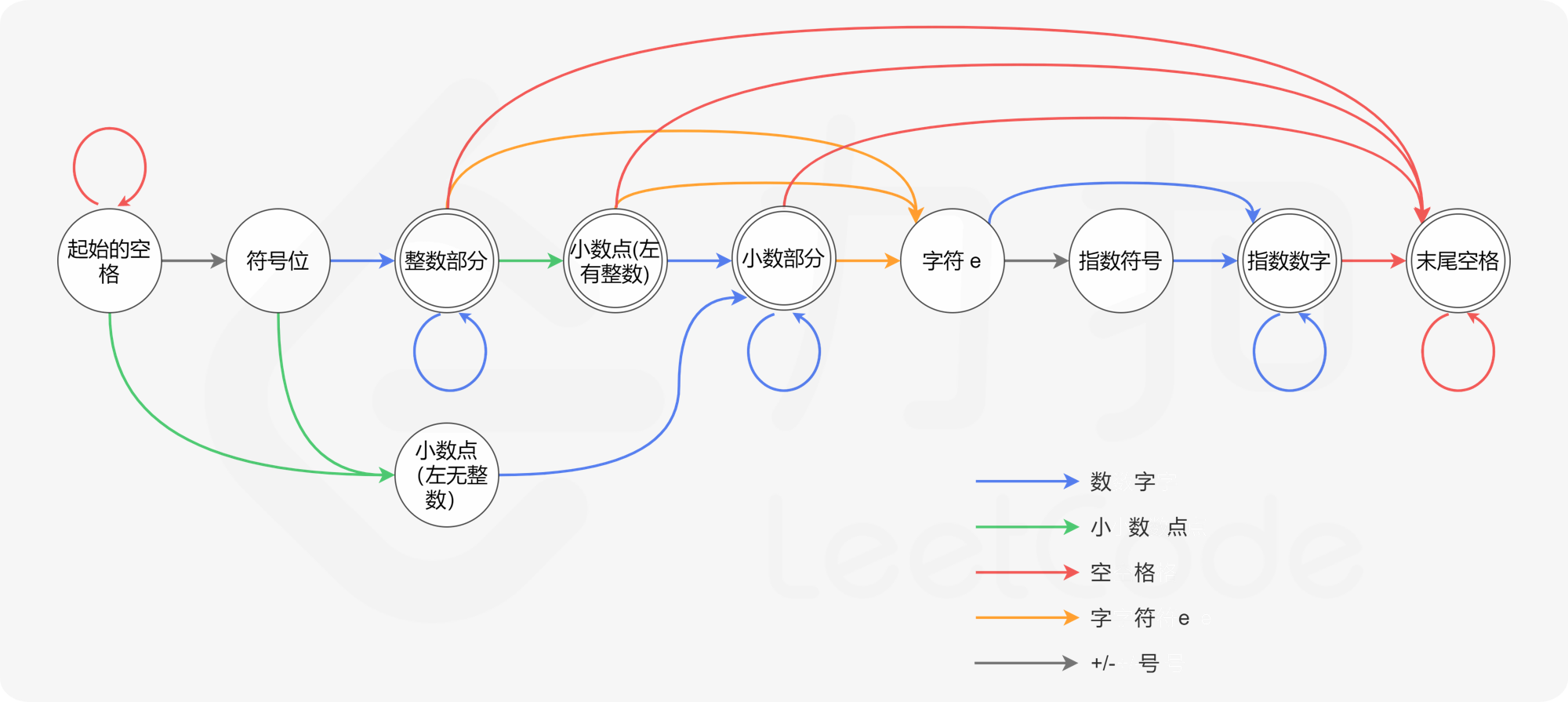
比较上图与「预备知识」一节中对自动机的描述,可以看出有一点不同:
我们没有单独地考虑每种字符,而是划分为若干类。由于全部 101010 个数字字符彼此之间都等价,因此只需定义一种统一的「数字」类型即可。对于正负号也是同理。
在实际代码中,我们需要处理转移失败的情况。例如当位于状态 1(起始空格)时,没有对应字符 e 的状态。为了处理这种情况,我们可以创建一个特殊的拒绝状态。如果当前状态下没有对应读入字符的「转移规则」,我们就转移到这个特殊的拒绝状态。一旦自动机转移到这个特殊状态,我们就可以立即判定该字符串不「被接受」。
实现
class Solution {public:enum State {STATE_INITIAL,STATE_INT_SIGN,STATE_INTEGER,STATE_POINT,STATE_POINT_WITHOUT_INT,STATE_FRACTION, //小数部分STATE_EXP, //指数eSTATE_EXP_SIGN,STATE_EXP_NUMBER,STATE_END,};enum CharType {CHAR_NUMBER,CHAR_EXP,CHAR_POINT,CHAR_SIGN,CHAR_SPACE,CHAR_ILLEGAL,};CharType toCharType(char ch) {if (ch >= '0' && ch <= '9') {return CHAR_NUMBER;} else if (ch == 'e' || ch == 'E') {return CHAR_EXP;} else if (ch == '.') {return CHAR_POINT;} else if (ch == '+' || ch == '-') {return CHAR_SIGN;} else if (ch == ' ') {return CHAR_SPACE;} else {//非法字符return CHAR_ILLEGAL;}}bool isNumber(string s) {unordered_map<State, unordered_map<CharType, State>> transfer{//{当前状态,{传入字符,下一状态}}{STATE_INITIAL, {{CHAR_SPACE, STATE_INITIAL},{CHAR_NUMBER, STATE_INTEGER},{CHAR_POINT, STATE_POINT_WITHOUT_INT},{CHAR_SIGN, STATE_INT_SIGN},}}, {STATE_INT_SIGN, {{CHAR_NUMBER, STATE_INTEGER},{CHAR_POINT, STATE_POINT_WITHOUT_INT},}}, {STATE_INTEGER, {{CHAR_NUMBER, STATE_INTEGER},{CHAR_EXP, STATE_EXP},{CHAR_POINT, STATE_POINT},{CHAR_SPACE, STATE_END},}}, {STATE_POINT, {{CHAR_NUMBER, STATE_FRACTION},{CHAR_EXP, STATE_EXP},{CHAR_SPACE, STATE_END},}}, {STATE_POINT_WITHOUT_INT, {{CHAR_NUMBER, STATE_FRACTION},}}, {STATE_FRACTION,{{CHAR_NUMBER, STATE_FRACTION},{CHAR_EXP, STATE_EXP},{CHAR_SPACE, STATE_END},}}, {STATE_EXP,{{CHAR_NUMBER, STATE_EXP_NUMBER},{CHAR_SIGN, STATE_EXP_SIGN},}}, {STATE_EXP_SIGN, {{CHAR_NUMBER, STATE_EXP_NUMBER},}}, {STATE_EXP_NUMBER, {{CHAR_NUMBER, STATE_EXP_NUMBER},{CHAR_SPACE, STATE_END},}}, {STATE_END, {{CHAR_SPACE, STATE_END},}}};int len = s.length();State st = STATE_INITIAL;for (int i = 0; i < len; i++) {CharType typ = toCharType(s[i]);if (transfer[st].find(typ) == transfer[st].end()) {return false;} else {st = transfer[st][typ];}}return st == STATE_INTEGER || st == STATE_POINT|| st == STATE_FRACTION || st == STATE_EXP_NUMBER || st == STATE_END;}};
复杂度分析
- 时间复杂度:
- 空间复杂度:
★★剑指 Offer 56 - II. 数组中数字出现的次数 II
思路
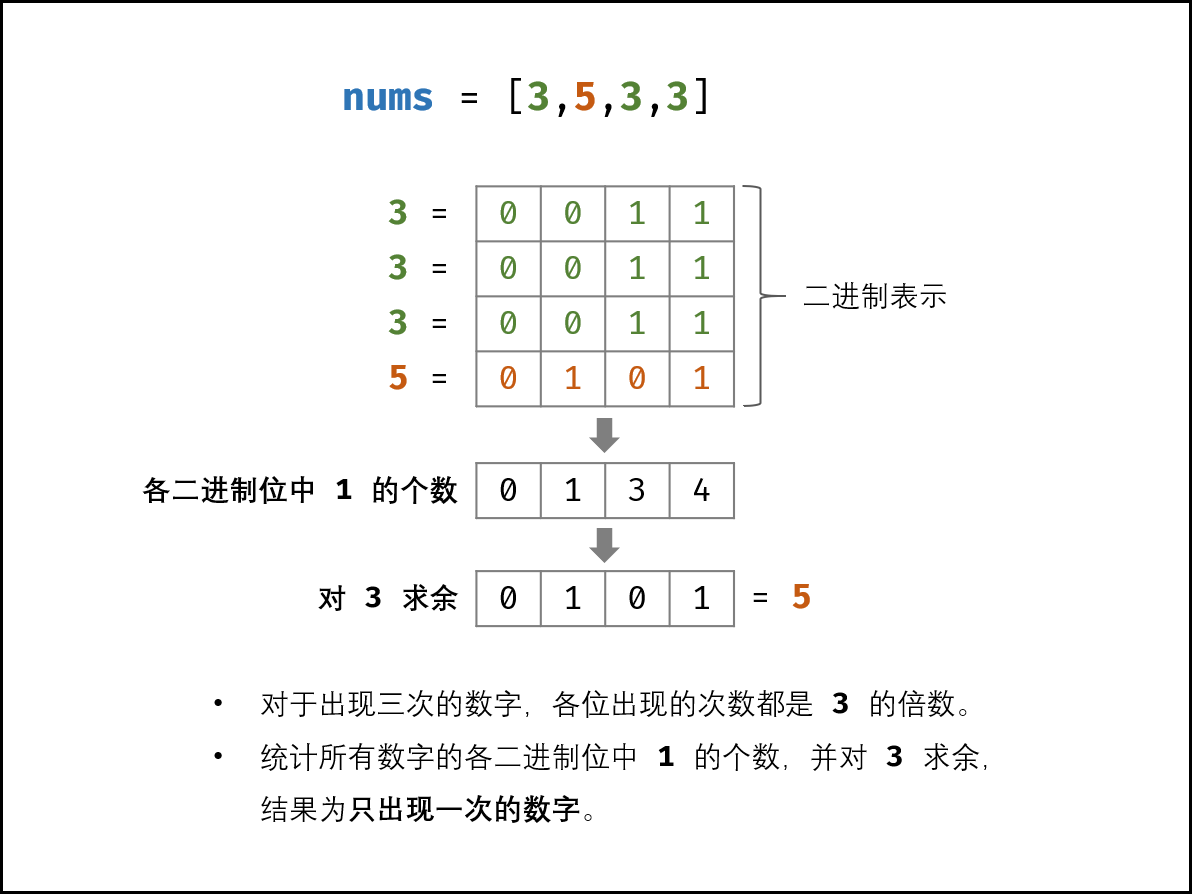
如下图所示,考虑二进制形式,对于出现三次的数字,各
二进制位出现的次数都是3的倍数。即统计所有数字中二进制位中1出现的次数,对3求余,即可得出现1次的数字。
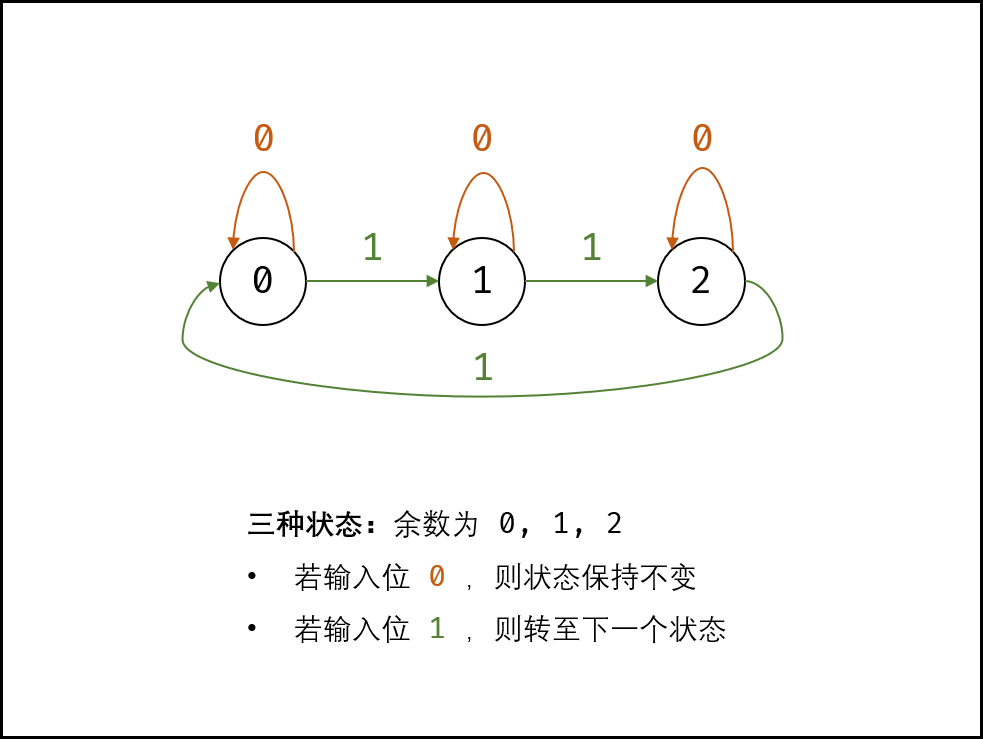
由于各二进制位的位运算规则相同,因此仅需考虑一位即可。对于所有数字中第i位中1的个数,存在三种状态(即对3求余后),【0,1,2,3】
- 状态转换方程如下:
由于二进制仅能表示两种状态,故采用2位二进制来表示如上状态转换,设两二进制位分别为two,one,如下: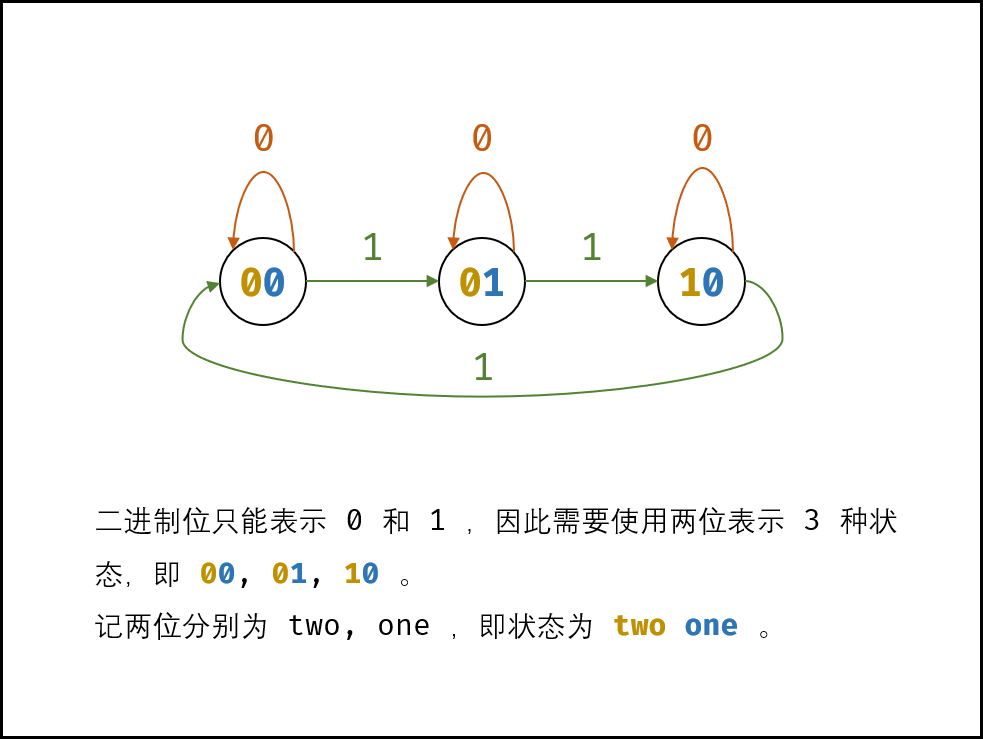
接下来,需要通过 状态转换表 导出 状态转换的计算公式 。首先回忆一下位运算特点,对于任意二进制位 x ,有:
- 异或:
x ^ 0 = x , x ^ 1 = ~x - 与:
x & 0 = 0 , x & 1 = x
状态转换表如下:
| n | two | one | two(next) | one(next) | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 0 |
让我们循序渐进来计算one和two:
计算one的方法:
#设当前状态为two one,输入二进制位n:if two == 0:if n == 0:one=oneif n == 1:#one=1->0#one=0->1one=~oneif two == 1:one=0# 加入异或运算if two==0:one=n^oneif two==1:one=0#加入与运算one=n ^ one & ~two#在one(next)的基础上,计算two可得two=n ^ two & ~one
总结:
以上是对二进制位i的分析,对于int类型的其余31位具有相同的运算规则,故将上述算法套用至所有32位数上。
遍历完所有数字后,各二进制为都出在状态00和状态01(此状态取决于“只出现1次的数”),而此两状态由one来决定(two恒为0),返回ones即可
算法
实现
def singleNumber(self, nums: List[int]) -> int:ones,twos=0,0for v in nums:ones = ones ^ v & ~twostwos = twos ^ v & ~onesreturn ones
复杂度分析
- 时间复杂度:
,每次循环的位运算为
,遍历数组为O(N)
- 空间复杂度:
题目标题难度划分
| 星级 | 题目难度 |
|---|---|
| ☆ | 简单 |
| ☆☆ | 中等 |
| ☆☆☆ | 困难 |
算法掌握难度程度划分
| 星级 | 掌握难度 |
|---|---|
| 无 | 普通 |
| ❤ | 经典,易掌握 |
| ❤❤ | 经典,略难掌握 |
| ❤❤❤ | 困难 |