14- ☆☆I. 剪绳子

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

❤❤递归——分治思想(注意如何计算复杂度)

思想

分治思想的解决方案往是递归，注意到当我们将一段绳子剪成2段时，其剩下部分仍能继续剪，也可以不剪。
假设F[n]为长度为n的绳子的最大乘积。则有

终止条件：n==2时，F[n]=1;

实现

int cuttingRope(int n){
    if(n==2) return 1;
    int ret=-1;
    for(int i=1;i<n;i++){
        ret=max(ret,max(i*cuttingRope(n-i),i*(n-i)));
    return ret;
    }
}

复杂度

• 时间复杂度：

• 空间复杂度：，栈空间最大深度为N

  记忆化

  思想

  上述时间复杂度过高，在于重复计算了F[i]，顾只需要记录F[i]便可大大减少复杂度

  实现

  int F[n]={0};
  F[2]=1;
  int cuttingRope(int n){
    if(F[n]!=0) return F[n];
    for(int i=1;i<n;i++){
        ret=max(ret,max(i*cuttingRope(n-i),i*(n-i)));
    F[n]=ret;
    return ret;
    }
  }

  复杂度分析

• 时间复杂度:

• 空间复杂度:,因为使用了f

  ❤❤动态规划

  思想

  同样的，采用动态规划，从已知值F[2]逐渐递归至F[n]

  算法

  建立一维动态数组dp:

• 边界条件：dp[1]=dp[2]=1,表示长度为2的绳子最大乘积为1

• 状态转移方程：dp[i] = max(dp[i], max((i - j) * j, j * dp[i - j]))，可以这样理解：

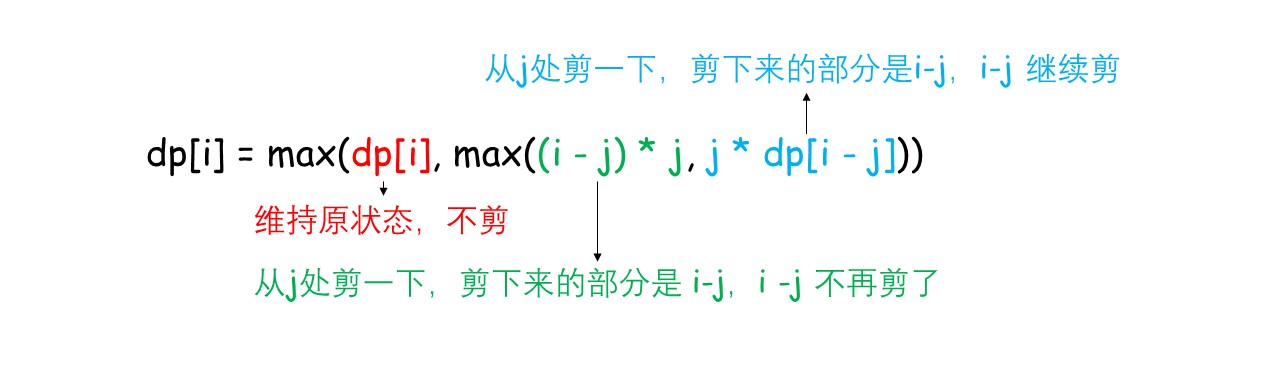
即将长度为i的绳子分为，剪去j，剩余i-j有两种情况，即剪与不剪

实现

int dp[n]={0};
dp[2]=1;
int cuttingRope(int n){
    for(int i=3;i<n;i++){
        for(int j=1;j<i;j++)
           dp[i]=max(dp[i],max((i-j)*j,j*dp[i-j]));
    }
    return dp[n];
}

复杂度分析

• 时间复杂度：
• 空间复杂度：

❤数学解法（熟悉方法，费事费时）

思想

数学推导

切分规则

算法

实现

int cuttingRope(int n){
    if(n<4) return n-1;
    int a=n/3,b=n%3;
    if(b==0){
        return pow(3,a);
    }
    else if(b==1){
        return pow(3,a-1)*4;
    }
    else{
        return pow(3,a)*2;
    }
}

复杂度分析

• 时间复杂度：
  • 求整和求余运算：资料提到不超过机器数的整数可以看作是 O(1)O(1)O(1) ；
  • 幂运算：查阅资料，提到浮点取幂为 O(1)O(1)O(1)
• 空间复杂度：