字典树又称前缀树，由多叉树形成主要包含如下2个部分：

  • 儿子数组：用于存储下一个节点（若字符集为’a’-‘z’：则儿子数组大小则为26，即最多为26叉树）
  • 结尾标识符
  • 方法
    • 插入（重点）
    • 查找

主要内容

字典树实现比较简单，最主要的便是【插入】的编写，如下将用代码实例结合图结构来讲解一下字典树
字典树主要有3个性质：

  1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符
  2. 从根节点到某一节点，路径上经过的字符连起来，为该节点对应的字符串
  3. 每个节点的所有子节点包含的字符串都不相同

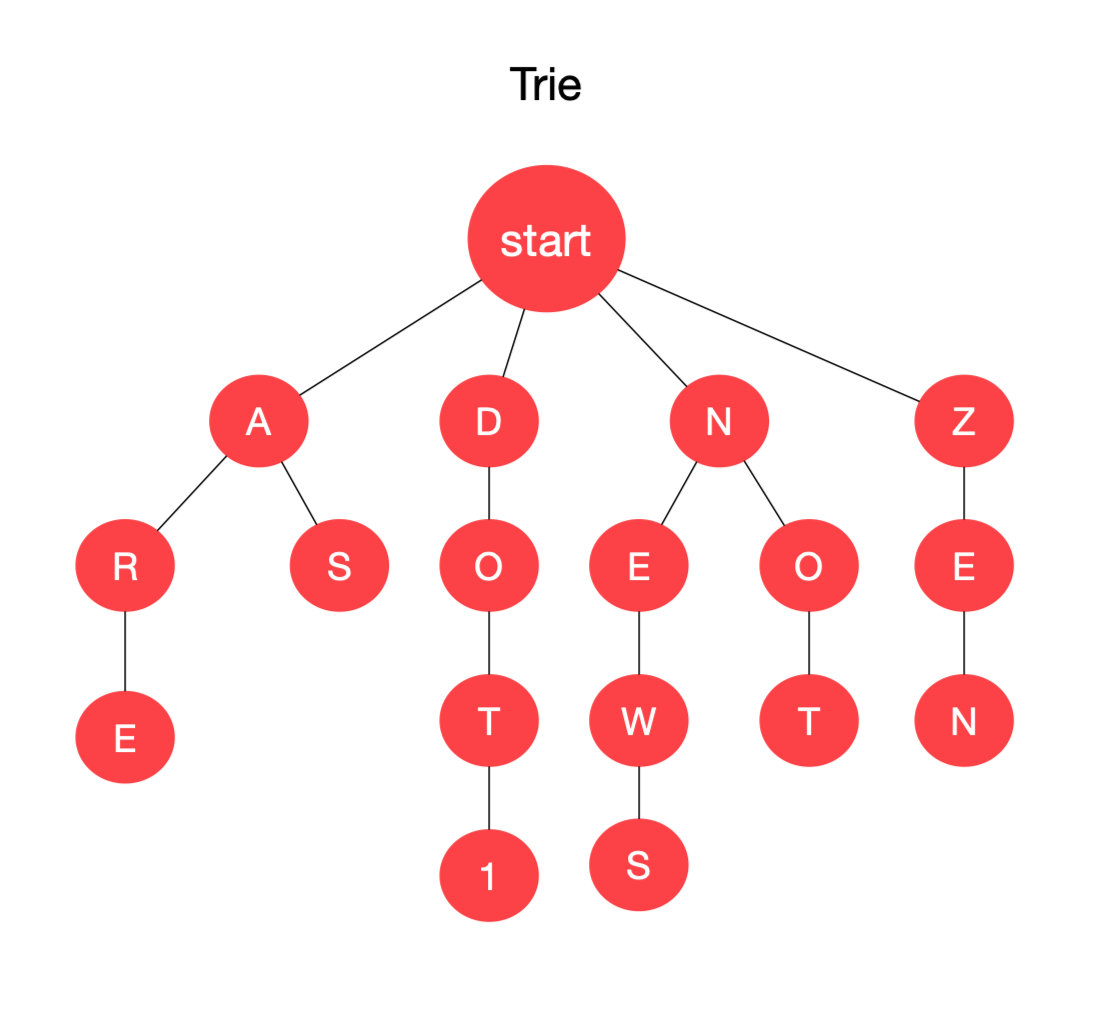
字典/前缀树 - 图1
算法思路：

  • 数据结构：
    树上每个节点均由【儿子数组】和【结尾符】组成。

  • 算法

    • 插入
    1. 按字母遍历单词
    2. 判定当前字母是否在儿子数组中
      1. 是，则继续递归遍历
      2. 否，创建新结点，按i继续操作
    3. 知道遍历到最后一个字母，将该字母对应的节点【结尾符】置真！
      1. /* 实例代码为一个单词字典树 */
      2. #include <vector>
      3. #include <string>
      4. using namespace std;
      5. class Trie {    
      6. bool isEnd;
      7. vector<Trie*> children;
      8. /* 查找 */
      9. Trie* searchPrefix(string& prefix){
      10.   Trie* node = this;
      11.   for (char ch : prefix) {
      12.       ch -= 'a';
      13.       if (node->children[ch] == nullptr) {
      14.           return nullptr;
      15.       }
      16.       node = node->children[ch];
      17.   }
      18.   return node;
      19. }
      20. public:
      21. Trie() :
      22.   isEnd(false),children(26,nullptr){}
      23. /* 插入 */
      24. void insert(string& word) {
      25.   Trie* cur = this;
      26.   for (auto ch : word) {
      27.       ch-='a';
      28.       if (cur->children[ch] == nullptr) {
      29.           cur->children[ch] = new Trie();
      30.       }
      31.       cur = cur->children[ch];
      32.   }
      33.   cur->isEnd = true;
      34. }
      35. /* 查找 */
      36. bool search(string& word){
      37.   Trie* node=searchPrefix(word);
      38.   return node!=nullptr && node->isEnd;
      39. }
      40. };

      复杂度分析

  • 时间复杂度:字典/前缀树 - 图2

  • 空间复杂度: 字典/前缀树 - 图3