设输入数组nums的众数为 x ,数组长度为 n 。
推论一: 若记 众数 的票数为+1 ,非众数 的票数为 −1 ,则一定有所有数字的 票数和 > 0 。
推论二: 若数组的前k个数字的票数和=0,则数组剩余(n-a)个数字的票数和一定仍>0,即后(n-a)个数字的众数仍为x;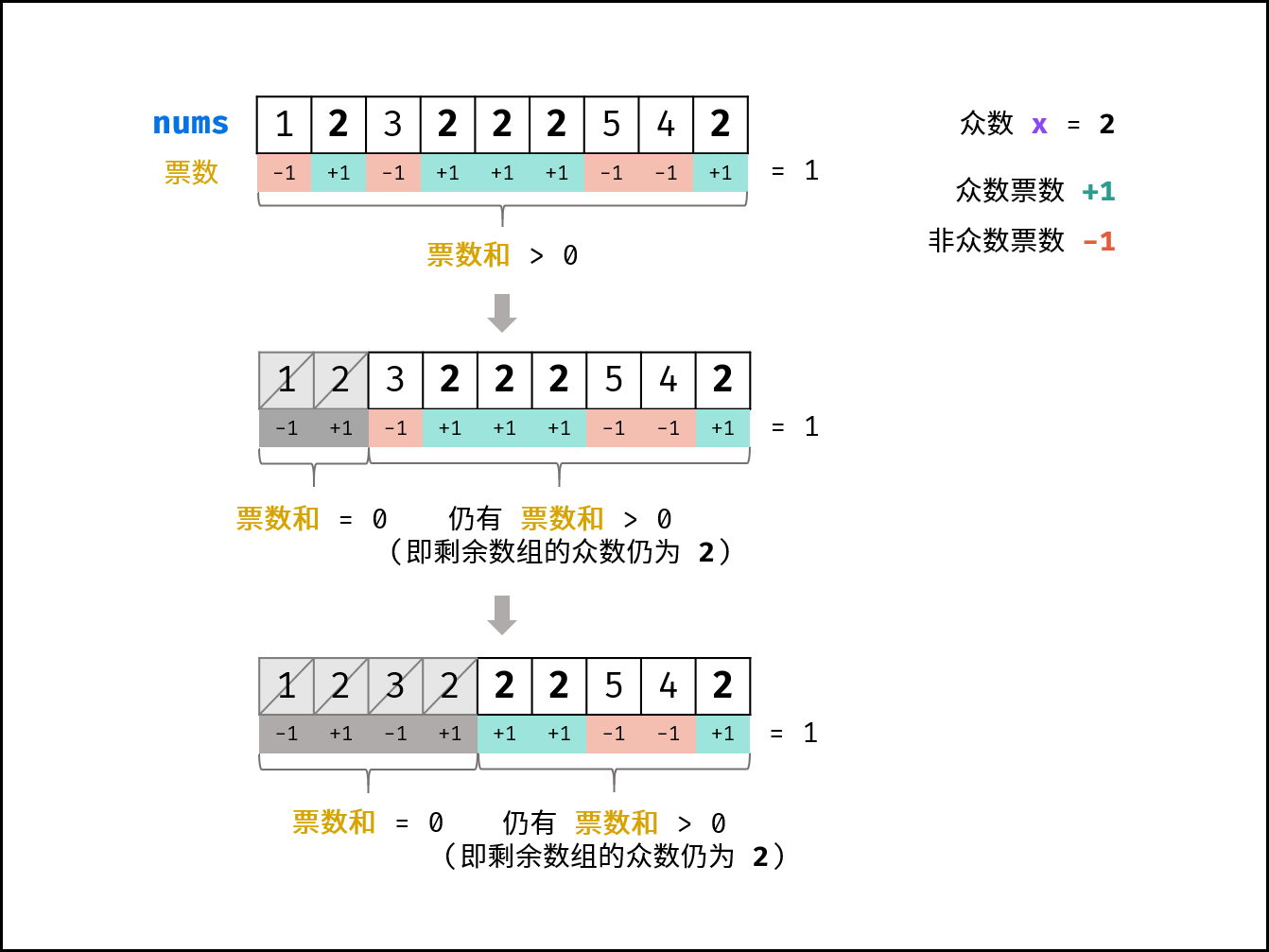
根据以上推论,假设数组首个元素 为众数,遍历并统计票数。当发生 票数和 =0 时,剩余数组的众数一定不变 ,这是由于:
故剩余数组的众数一定不变。
利用上述假设,每次票数和=0时,便可缩小区间,最终区间的假设众数便为真众数。
剑指 Offer 39. 数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
摩尔投票法
实现
int majorityElement(vector<int>& nums) {int x=nums[0],votes=0;for(int i=0;i<nums.size();i++){if(nums[i]==x) ++votes;else --votes;if(!votes){//显然若存在众数,必然当i=num.size()-1时,votes!=0x=nums[i+1];}}}
复杂度分析
- 时间复杂度:
- 空间复杂度:
算法2
思路
算法
实现
复杂度分析
- 时间复杂度:
- 空间复杂度:
题目标题难度划分
| 星级 | 题目难度 |
|---|---|
| ☆ | 简单 |
| ☆☆ | 中等 |
| ☆☆☆ | 困难 |
算法掌握难度程度划分
| 星级 | 掌握难度 |
|---|---|
| 无 | 普通 |
| ❤ | 经典,易掌握 |
| ❤❤ | 经典,略难掌握 |
| ❤❤❤ | 困难 |

