参考：

https://www.cnblogs.com/w4ngzhen/p/13817077.html

BNF范式（巴科斯范式）简介

BNF 规定是推导规则(产生式)的集合，写为：
<符号> ::= <使用符号的表达式>
这里的 <符号>是非终结符，而表达式由一个符号序列，或用指示选择的竖杠'|' 分隔的多个符号序列构成，每个符号序列整体都是左端的符号的一种可能的替代。从未在左端出现的符号叫做终结符。

编译原理文法定义为四元集 非终结符集合
终结符集合
产生式集合 START 闭包与正闭包： ∑的正闭包： ∑+=∑∪∑2∪∑3∪∑4∪…… ∑的克林闭包（kleene Closure）： ∑=∑0∪∑+（与正闭包区别哦，这算是新概念） 例如：{0,1}+ = {0，1，00，01，11，000，001，010，011，100，……} {0,1} = {ε，0，1，00，01，11，000，001，010，011，100，…}

S_型文法

• 每个产生式的右部都以终结符开始
• 同一非终结符的各个候选式的首终结符不同

例子如下：

显然符合上述特点
对于字符串abc，可得到如下推导

即对于每个读入的字符，S_型文法可直接确定对应的产生式。
对于流程第2部，

FOLLOW集

非终结符的后继符号集，即 可能在某个句型中紧跟在后边的终结符的集合，记为

为了解决产生式问题。即当前某终结符的产生式右部的首字符与输入不匹配时，若存在,则检查是否存在于的后续符号集，若在其中，则继续匹配，否则报错。

SELECT集

可选用该产生式，进行推导时的，输入符号的集合

解释：

• : 即用该产生式进行推导时， 对应的输入符号是，

• 非终结符A推导至终结符, 则对应输入符号集合为，A的后续符号集合

  q_文法

• 每个产生式的右部以或终结符开始

• 具有相同左部的产生式，有不可相交的可选集

  FIRST集

  该集合存储产生式右部的串（无论是、终结符、非终结符）的所有串首为终结符的集合。

LL(1)型文法

定义

对于情况1，反证法如下，若 均不能推导出,假设两者的串首终结符集的交集不为空，那么对于某个输入字符c，到底该选择哪一个产生式呢？显然出现了二义性，故交集为空
对于情况2，反证法如下，若 均能推导出，假设，对于某个输入字符c，需要靠来判断选择哪一个产生式，故由于交集非空，产生二义性，故交集为空

进一步分析

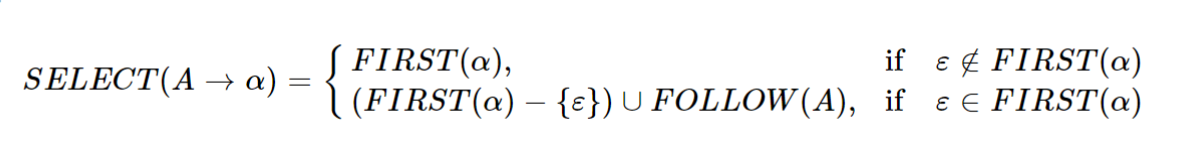
由上述情况2可知， ，且 ，为了保证不出现二义性，确保
,此处

,显然情况2得