剑指 Offer 33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回
true,否则返回false。假设输入的数组的任意两个数字都互不相同。
DFS
思路
采用分治算法,若该数组可以生成搜索树,则其左右子树也是搜索树。由于后序遍历顺序为【左右根】,故最后一个节点必然为根节点,且遍历数组到第一个>根节点的点必然为右子树中的最左的点,故可以得到左右子树对应的子数组。
对于二叉搜索树,满足【左<根<右】,故依据划分点判断是否满足上述条件,若满足则继续【划分】,若不满足则return false;
算法
recur(i,j):
i,j表示子树的范围
- 遍历
[i,j]范围内的数组,找到第一个>postorder[j]的位置,记该位置为m - 判断
[m,j-1]内的节点是否>postorder[j],若不满足,则return,若满足,则继续第三步 - recur(i,m-1) && recur(m,j-1);
边界条件:
- 若i>=j,显然可以构造搜索树,返回true;
实现
```cpp bool recur(vector& order,i,j){ if(i>=j) return true; int rootVal=order[j],m=i; while(order[m]<=rootVal) ++m; for(int k=m;k<j;k++){
} return recur(order,i,m-1) && recur(order,m,j-1); }if(order[m]<rootVal) return false;
<a name="7k4jf"></a>## 复杂度分析- 时间复杂度:,最差的情况,每次recur减去一个节点,即递归占用O(N);每轮递归都需要遍历所有节点,占用O(N);- 空间复杂度:,最差情况下,树退化为链表,递归深度达到O(N)<a name="jxlcG"></a>## ❤❤❤单调栈<a name="i7EcZ"></a>### 思路- **后序遍历倒序**: `[ 根节点 | 右子树 | 左子树 ]` 。类似 先序遍历的镜像 ,即先序遍历为 “根、左、右” 的顺序,而后序遍历的倒序为 “根、右、左” 顺序。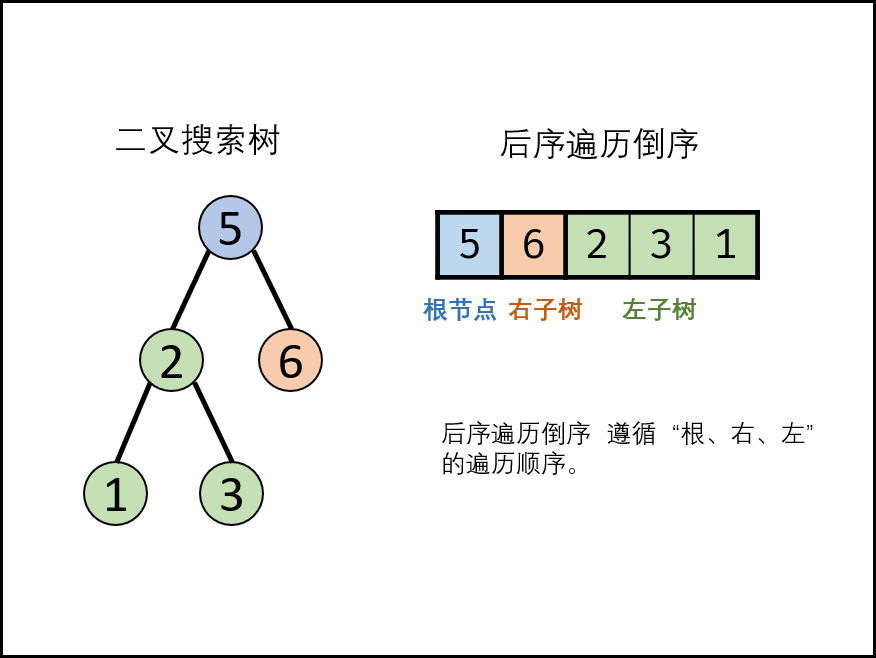- 设后续遍历的倒序列表为[],遍历此列表,设索引值i,若为二叉搜索树,则- - - 当遍历倒序后序时,若遭遇,则后续遍历的任意节点[]。> 节点仅有两种情况:1.为的左右子树节点,2.当root为右子树节点时,为root的父节点或更高层父节点的左子树各节点- 遍历“后序遍历的倒序列表”会多次遇到递减节点则可判定为二叉搜索树- 考虑以上特性,借助“**单调栈**”实现。1. 借助一个单调栈存储递增的节点;1. 每当遇到递减节点,则通过栈来更新父节点root.1. 每轮判断:1. 1. <a name="hmeVu"></a>### 算法1. **初始化**:单调栈stack,1. **倒序遍历**:记每个节点为1. **判断:**1. **更新父节点:**当栈不空时且,循环执行出栈,将出栈节点赋值给root。1. **入栈:将入栈**3. 若遍历完成,则返回true;<a name="CvnWR"></a>### 实现```cppbool verifyPostorder(vector<int>& postorder) {stack<int> mtStack;int root=INT_MAX;for(int i=postorder.size()-1;i>-1;i--){if(postorder[i]>root) return false;while(!mtStack.empty() && mtStack.top()>postorder[i]){root=mtStack.top();mtStack.pop();}mtStack.push(postorder[i]);}return true;
复杂度分析
- 时间复杂度:
- 空间复杂度:
,最差的情况,全部都是递减,单调栈存储所有节点
题目标题难度划分
| 星级 | 题目难度 |
|---|---|
| ☆ | 简单 |
| ☆☆ | 中等 |
| ☆☆☆ | 困难 |
算法掌握难度程度划分
| 星级 | 掌握难度 |
|---|---|
| 无 | 普通 |
| ❤ | 经典,易掌握 |
| ❤❤ | 经典,略难掌握 |
| ❤❤❤ | 困难 |

