题目名称
请实现
copyRandomList函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个next指针指向下一个节点,还有一个random指针指向链表中的任意节点或者null。示例 1:
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
哈希表
思路
由题意知,对于该链表的赋值,难点在于链表random节点的复制, 需要构建源节点和复制节点之间的映射关系,才可以得到复制random节点。
利用哈希表的查询特点,考虑构建 原链表节点 和 新链表对应节点 的键值对映射关系,再遍历构建新链表各节点的 next 和 random 引用指向即可。
算法
- 初始化:unordered_map;
- 在新空间中构建节点,并在哈希表中存储【源节点,复制节点】的映射关系
构建复制空间的random节点:
- copyNode=umap[orgNode]
- copyNode->random=umap[orgNode->random]
实现
Node* copyRandomList(Node* head){unordered_map<Node*,Node*> umap;//构建复制空间节点Node* cur=head;while(cur!=nullptr){Node* node=new Node(cur->val);umap.insert(make_pair(cur,node));cur=cur->next;}//构建复制空间节点的关系cur=head;while(cur!=nullptr){umap[cur]->next=umap[cur->next];umap[cur]->random=umap[cur->random];cur=cur->next;}return umap[head];}
复杂度分析
时间复杂度:
- 空间复杂度:
❤❤❤拼接+拆分
思路
考虑构建 原节点 1 -> 新节点 1 -> 原节点 2 -> 新节点 2 -> …… 的拼接链表,如此便可在访问原节点的 random 指向节点的同时找到新对应新节点的 random 指向节点.
算法
- 复制各节点,实现拼接
- 构建复制空间中中新节点的
random- 源节点为cur,复制节点为
copy=cur->next;则copy->random=cur->random->next;
- 源节点为cur,复制节点为
- 拆分原节点和复制节点
cur->next=copy->next;cur=cur->next;copy->next=cur->next;copy=copy->next;实现
Node* copyRandomList(Node* head) {Node* cur=head;if(head==NULL) return cur;Node* next=cur->next;//拼接while(cur!=NULL){Node* node = new Node(cur->val);cur->next=node;node->next=next;cur=next;if(cur!=NULL) next=cur->next;}//构建复制节点的random关系cur=head;Node* ansCur=cur->next;while(cur!=NULL){if(cur->random!=NULL) ansCur->random=cur->random->next;cur=ansCur->next;if(cur!=NULL) ansCur=cur->next;}//拆分cur=head;copy=cur->next;Node* ans=head->next;while(cur!=NULL){cur->next=copy->next;cur=cur->next;if(cur!=NULL) copy->next=cur->next;copy=copy->next;}return ans;}
复杂度分析
- 时间复杂度:
3次遍历,时间复杂度为
- 空间复杂度:
图的基本单元是 顶点,顶点之间的关联关系称为 边,我们可以将此链表看成一个图:
需要实现原节点与复制节点之间的映射关系
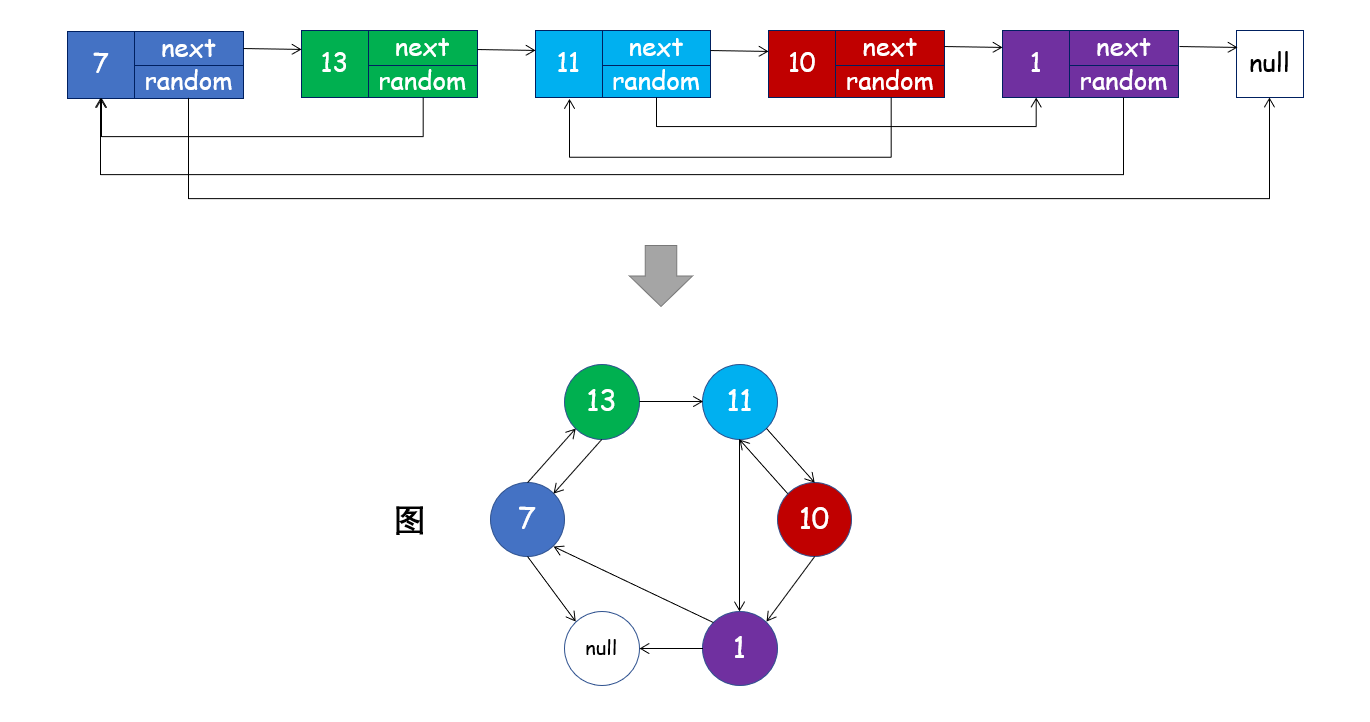 由于图的遍历方式有深度优先搜索和广度优先搜索,同样地,对于此链表也可以使用深度优先搜索和广度优先搜索两种方法进行遍历。
由于图的遍历方式有深度优先搜索和广度优先搜索,同样地,对于此链表也可以使用深度优先搜索和广度优先搜索两种方法进行遍历。
DFS
实现
def copyRandomList(self, head: 'Node') -> 'Node':def dfs(head):if not head: returnif head in visited:return visited[head]#创建新节点copy=Node(head.val,None,None)visited[head]=copycopy.next=dfs(head.next);copy.random=dfs(head.random);return copy;visited={}return dfs(head)
复杂度分析
- 时间复杂度:
-
BFS
实现
Node* copyRandomList(Node* head) {if(!head) return NULL;unordered_map<Node*,Node*> umap;queue<Node*> q;Node* copy=new Node(head->val);q.push(head);umap[head]=copy;while(!q.empty()){Node* cur=q.front();q.pop();if(cur->next!=NULL && umap.find(cur->next)==umap.end()){umap[cur->next]=new Node(cur->next->val);q.push(cur->next);}if(cur->random!=NULL && umap.find(cur->random)==umap.end()){umap[cur->random]=new Node(cur->random->val);q.push(cur->random);}umap[cur]->next=umap[cur->next];umap[cur]->random=umap[cur->random];}return umap[head];}
复杂度分析
时间复杂度:
- 空间复杂度:
题目标题难度划分
| 星级 | 题目难度 |
|---|---|
| ☆ | 简单 |
| ☆☆ | 中等 |
| ☆☆☆ | 困难 |
算法掌握难度程度划分
| 星级 | 掌握难度 |
|---|---|
| 无 | 普通 |
| ❤ | 经典,易掌握 |
| ❤❤ | 经典,略难掌握 |
| ❤❤❤ | 困难 |

