（递归）复杂度分析

汉诺塔

汉诺塔大家肯定都玩过，规则也很简单：有 A, B, C 三根柱子，上面穿有从大到小排列的圆盘，现在你需要借助 B 柱把 A 柱上的圆盘挪到 C 柱上，一次只能挪一个，且大的圆盘不能放在小的圆盘的上面。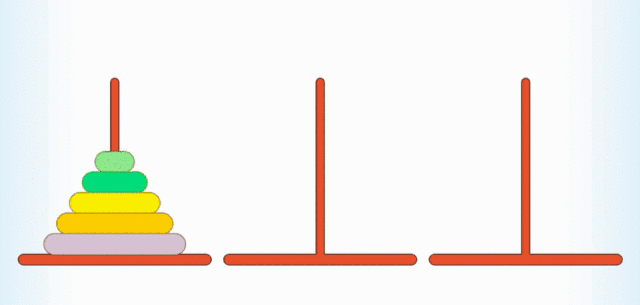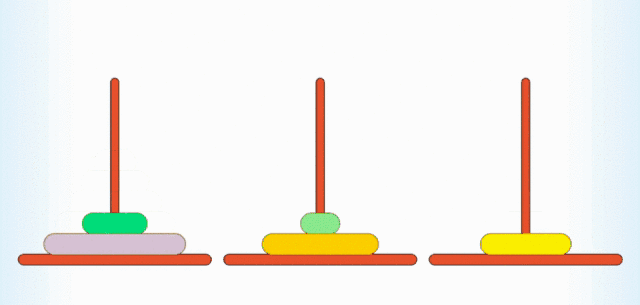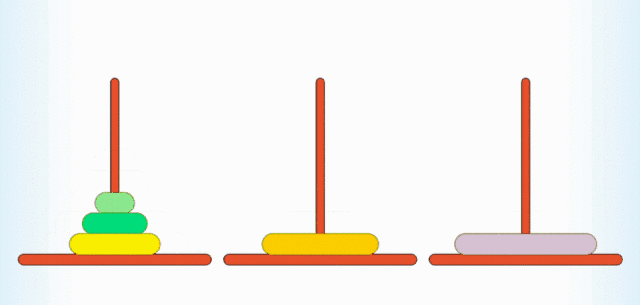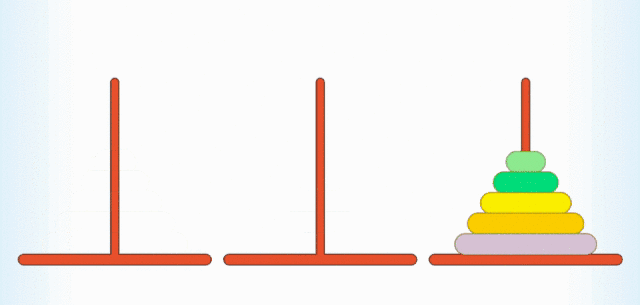

汉诺塔跟递归有什么关系呢？如果你是一个细心观察的人，你就会发现，要想把 个圆盘从 A 柱挪到 C 柱上，你首先要通过某种方法把 个柱子从 A 挪到 B 柱上，给 A 柱上最大的圆盘“腾位置”，然后把最大的圆盘从 A 柱移动到 C 柱上，最后再通过某种方法把 B 柱上 个圆盘挪到 C 柱上。至于怎么移动这 个柱子，我们可以又用某种方法移动最上面的 个柱子，给第二大的圆盘“腾位置”，再将 个柱子移动到相应的柱子上。这样我们便可以一直递归下去，直到出现递归出口，也就是只有一个圆盘的情况。
我们用几张图来直观地理解一下，假设这里有 4 个圆盘，我们可以分为三个步骤：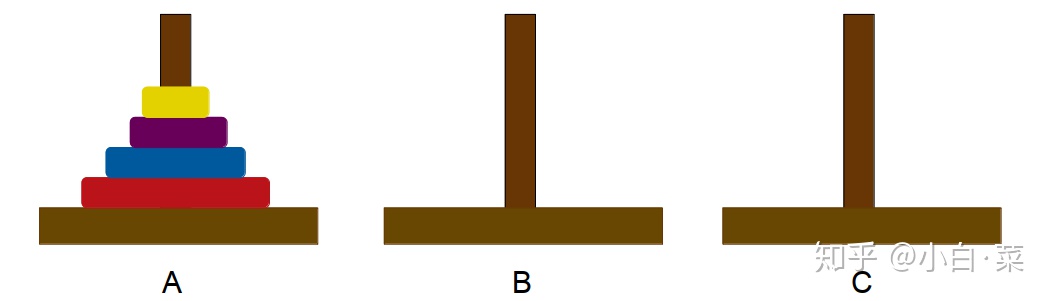

• 步骤一：用某种方法将 3 个圆盘从 A 柱移动到 B 柱

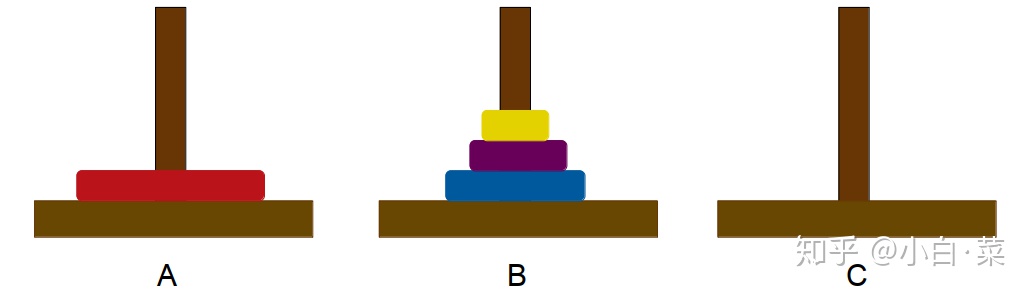
• 步骤二：将 A 柱的圆盘移动到 C 柱

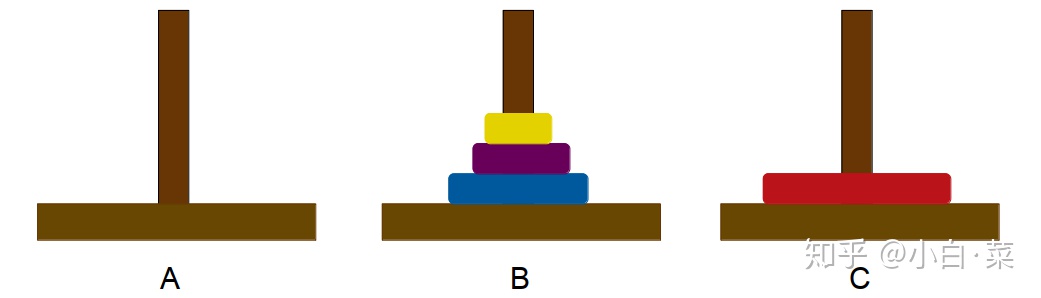
• 步骤三：再用某种方法将 3 个圆盘从 B 柱移动到 C 柱

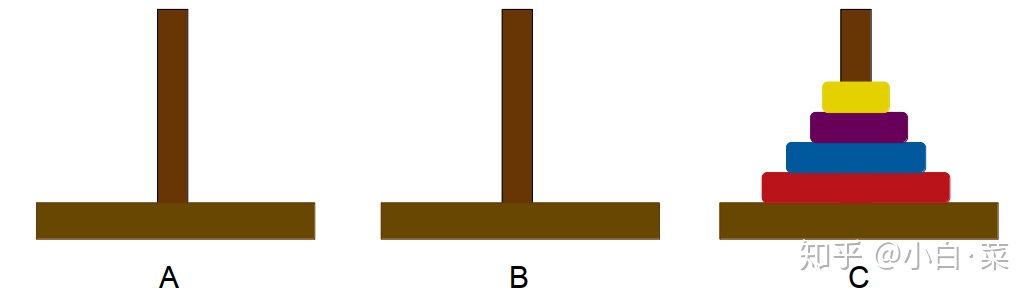
那么怎样来写递归关系式呢？我们看到，要解决 阶汉诺塔的问题，我们先要解决两个 阶同样的问题，外加一个单次移动。所以我们的递归关系式应该这样写：

我们还是采用回代的方式解出这个关系式：

复杂度为 ，最后我们用代码来实现一下吧。