https://www.zhihu.com/question/21923021

KMP算法解决的是：字符串（主串,T串）中模式的定位问题！，即关键词（模式，P串）搜索。
image.png
典型的关键词搜索，可以使用暴力法，每次从头遍历，进行匹配，但复杂度显然不可忍受，故有个大神就利用已匹配过的信息，来优化整个模式串的匹配过程。

从头思考

如何高效的利用已经匹配的信息呢？

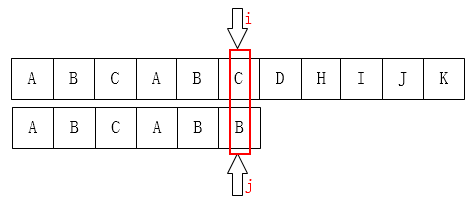
  1. 当匹配进程递进时，到j时匹配失败，如何在保持i不变的情况下，更新j呢?

KMP算法——关键词搜索 - 图2
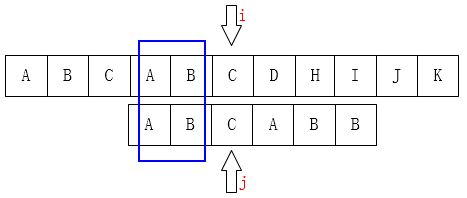
2. 按照人的思维，应该将j移动至第1位（因为i处有A已经匹配过啦），如下

KMP算法——关键词搜索 - 图3

下图例子也相同 KMP算法——关键词搜索 - 图4

可以把j指针移动到第2位，因为前面有两个字母是一样的：
KMP算法——关键词搜索 - 图5

结论-1

设j的下一个移动位置为k,由归纳可知。有
KMP算法——关键词搜索 - 图6

为何模式串中的前k个元素不需要进行比较（因为j直接跳到k，进行后续的匹配了，所以前k个元素不用比较），证明如下： 当匹配进程到T[i],P[j]时中断，有如下关系式： KMP算法——关键词搜索 - 图7可得KMP算法——关键词搜索 - 图8， 显然当j移动到位置k时，模式串中前k个元素不需要比较。

显然，P中每一个位置都有可能发生不匹配，故需要计算每一个位置j对应的k，故采用next[j]=k来保存信息。

next数组

next数组是对于模式串而言的。P 的 next 数组定义为：next[i] 表示 P[0] ~ P[i] 这一个子串，使得 前k个字符恰等于后k个字符 的最大的k. 特别地，k不能取i+1（因为这个子串一共才 i+1 个字符，自己肯定与自己相等，就没有意义了）。

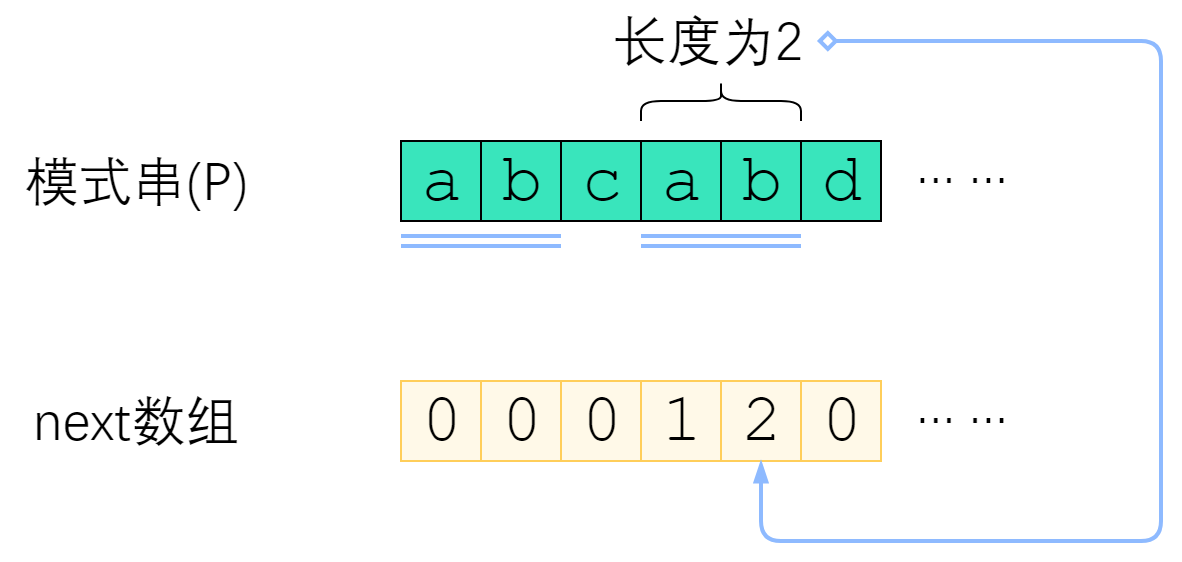
image.png
上图给出了一个例子。P=”abcabd”时，next[4]=2，这是因为P[0] ~ P[4] 这个子串是”abcab”，前两个字符与后两个字符相等，因此next[4]取2. 而next[5]=0，是因为”abcabd”找不到前缀与后缀相同，因此只能取0.

如果把模式串视为一把标尺，在主串上移动，那么 Brute-Force 就是每次失配之后只右移一位；改进算法则是每次失配之后，移很多位，跳过那些不可能匹配成功的位置。但是该如何确定要移多少位呢？

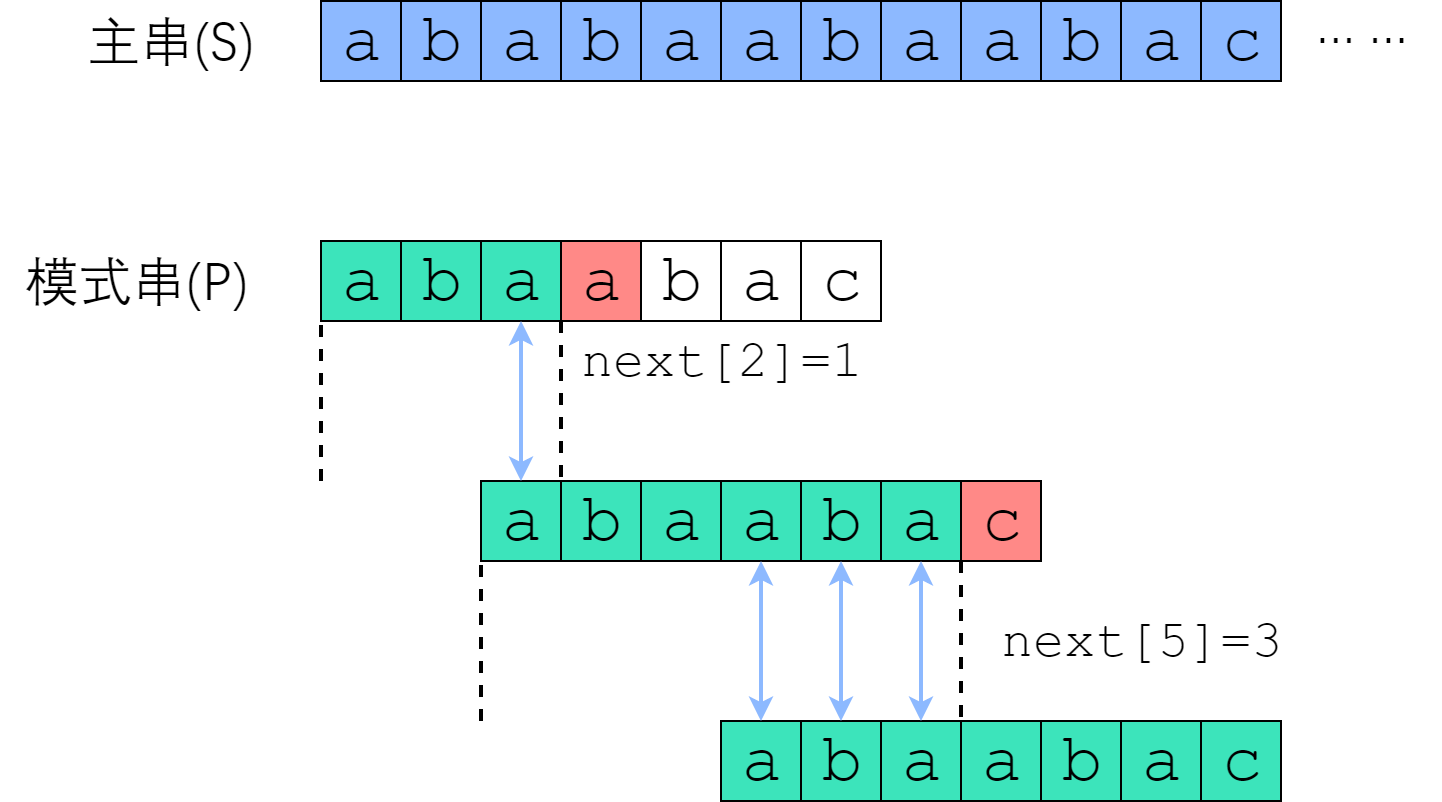
image.png
在 S[0] 尝试匹配，失配于 S[3] <=> P[3] 之后，我们直接把模式串往右移了两位，让 S[3] 对准 P[1]. 接着继续匹配，失配于 S[8] <=> P[6], 接下来我们把 P 往右平移了三位，把 S[8] 对准 P[3]. 此后继续匹配直到成功。
我们应该如何移动这把标尺？很明显，如图中蓝色箭头所示，旧的后缀要与新的前缀一致（如果不一致，那就肯定没法匹配上了）！

回忆next数组的性质：P[0] 到 P[i] 这一段子串中，前next[i]个字符与后next[i]个字符一模一样。既然如此，如果失配在 P[r], 那么P[0]~P[r-1]这一段里面，前next[r-1]个字符恰好和后next[r-1]个字符相等——也就是说，我们可以拿长度为 next[r-1] 的那一段前缀，来顶替当前后缀的位置，让匹配继续下去！
您可以验证一下上面的匹配例子：P[3]失配后，把P[next[3-1]]也就是P[1]对准了主串刚刚失配的那一位；P[6]失配后，把P[next[6-1]]也就是P[3]对准了主串刚刚失配的那一位。

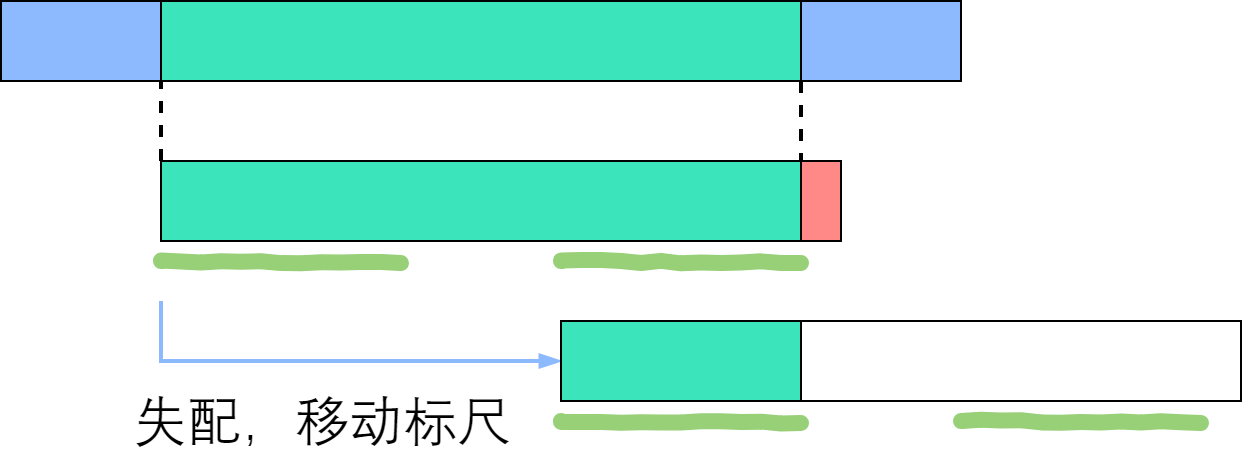
image.png
如上图所示，绿色部分是成功匹配，失配于红色部分。深绿色手绘线条标出了相等的前缀和后缀，其长度为next[右端]. 由于手绘线条部分的字符是一样的，所以直接把前面那条移到后面那条的位置。因此说，next数组为我们如何移动标尺提供了依据。接下来，我们实现这个优化的算法。

核心代码

  1. //next[i]=k指的是：
  2. //P[0...i]中前k个字符恰等于后k个字符
  3. vector<int> get_next(const string& p)
  4. {
  5.     vector<int> next(p.size());
  6.     next[0] = 0;
  7.     int k = 0;
  8.     for(int i=1;i<p.size();++i)
  9.     {
  10.         while (k > 0 && p[k] != p[i])    //若此时不匹配，循环返回直到匹配或k=0;
  11.             k = next[k - 1];
  12.         if (p[k] == p[i])                //若前缀匹配后缀，则++k；
  13.             ++k;
  14.         next[i] = k;                    //更新当前next
  15.     }
  16.     return next;
  17. }

循序渐进

上述代码直接看基本上看不懂，先来一步一步推导看看，显然next[j]的值表示，当T[i]!=P[j]时，j指针下一步移动的位置。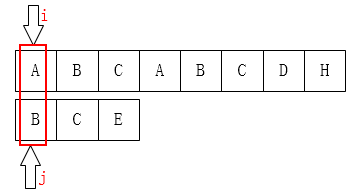
KMP算法——关键词搜索 - 图12
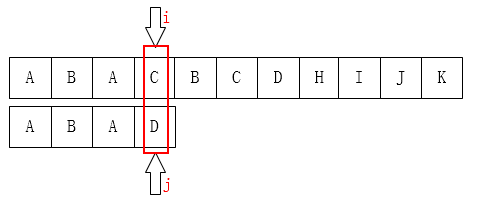
上图，j=0时不匹配，j的指针如何移动？
显然j已经在最左侧，如何保证P[0,k-1]=P[j-k,j-1]？故此时只能**i**指针后移。故这也是为何next[0]=-1的原因；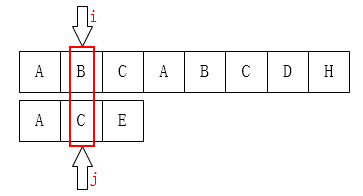
KMP算法——关键词搜索 - 图13
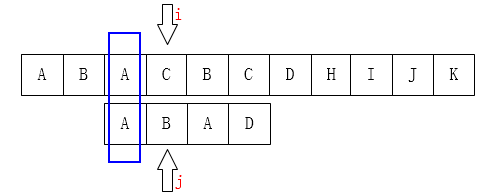
当j=1时，显然j指针只能前移到0位置。

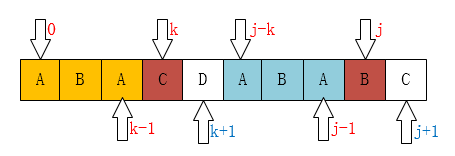
请仔细看如下两图

image.png
此时**P[k]=P[j]**,
已知next[j]=k,即j需要前移到k位置，那么显然next[j+1]=k+1;

证明： 已知P[0~k-1]=P[j-k~j-1], next[j]=k 现有P[k]=P[j],----------->P[0~k]=P[j-k~j], 归纳证明可得next[j]=k+1

———————————————————————————————————————————————————-
KMP算法——关键词搜索 - 图15
那么若**P[k]!=P[j]:**
从代码上看，此时有k=next[k];更新k,等待下一个P[j]==P[k]时更新对应的next[j]=k+1

解析代码k=next[k]： KMP算法——关键词搜索 - 图16 由于移动位置k是通过部分匹配值求得，故此时对于后缀”ABAB”来说，无对应前缀，但对于[ABA]来说，存在前缀，故此过程像定位”ABAC”模式串，当C和主串不同时，将指针移动至next[k];

现在已知kmp算法原理，可以写写看试试

  1. //求取匹配的多个位置
  2. vector<int> kmp(const string& t, const string& p)
  3. {
  4.     int j = 0;
  5.     auto next = get_next(p);
  6.     vector<int> ans;
  7.     for(int i=0;i<t.size();++i)
  8.     {
  9.         while (j > 0 && t[i] != p[j])                //不匹配时取上一个匹配位置
  10.             j = next[j - 1];
  11.         if (t[i] == p[j])                            //匹配
  12.             ++j;
  13.         if (j == p.size())
  14.         {
  15.             ans.push_back(i + 1 - j);                //存取主串的匹配首索引
  16.             j = next[j - 1];
  17.         }
  19.     }
  20.     return ans;
  21. }
  23. /**
  24. 示例：t="aaa",p="aa";
  25. --->ans={0,1};
  26. 即可匹配多次！
  27. */

相关题目

214. 最短回文串