对于链表相关问题,有如下几类：

• 排序（归并（B2U,U2B））
• 判环，环起点，环长度（快慢指针）

对于链表O(1)的算法，有如下：

• Floyd判圈算法（快慢指针）

排序链表（自顶向下、自底向上）

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

进阶： 你可以在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序吗？

算法（归并排序，自顶向下）

• 分解：待排序的区间为[l,r]，令m=l+((r-l)>>1),将区间分为[l,m],[m+1,r]，链表可用快慢指针寻终点
• 解决：使用归并排序递归地排序两个子序列（即当前节点数为1或0时，直接返回）
• 合并：把两个已经排好序的子序列[l,m]和[m+1,r]合并起来

实现

/* Merge */
ListNode* merge(ListNode* lhs,ListNode* rhs){
    /* merge two sorted list*/
    ListNode* dummyHead=new ListNode(0);
    auto tmp=dummyHead,tmp1=lhs,tmp2=rhs;
    while(tmp1!=nullptr && tmp2!=nullptr){
        if(tmp1->val<=tmp2->val){
            tmp->next=tmp1;
            tmp1=tmp1->next;
        }else{
            tmp->next=tmp2;
            tmp2=tmp2->next;
        }
        tmp=tmp->next;
    }
    if(tmp1){
        tmp->next=tmp1;
    }else{
        tmp->next=tmp2;
    }
    return  dummyHead->next;
}
/* divide and solve */
ListNode* sortList(ListNode* head){
    if(head==nullptr ||head->next==nullptr)
        return head;
    auto slow=head,fast=head;
    while(fast!=nullptr){
        fast=fast->next;
        if(fast!=nullptr){
            fast=fast->next;
        }
        if(fast==nullptr) break;    /* important !*/
        slow=slow->next;
    }
    auto next_head=slow->next;
    slow->next=nullptr;
    return merge(sortList(head),sortList(next_head));
}

复杂度分析

• 时间复杂度:

• 空间复杂度:，即递归栈的长度

  算法（归并排序，自低向顶，主动分解）

• 分解：将待排序的区间主动分解，按sublen逐渐以2指数递增

• 解决：使用归并排序递归地排序两个子序列（即当前节点数为1或0时，直接返回）

• 合并：把两个已经排好序的子序列[l,m]和[m+1,r]合并起来

  实现

  ListNode* sortListBottom2Up(ListNode* head) {
    int len=0;
    auto tmp=head;
    while(tmp!=nullptr){
        tmp=tmp->next;
        len++;
    }
    auto assi_node=new ListNode(0,head);
    for(int sublen=1;sublen<len;sublen<<=1){
        auto head_tmp=assi_node->next,assi_node_tmp=assi_node;
        while(head_tmp!=nullptr){
            /* get first head of first segment, len = sublen */
            auto first=head_tmp,tmp1=first;
            for(int i=1;i<sublen && tmp1->next!=nullptr;i++){
                tmp1=tmp1->next;
            }
            /* get second head of second segment, len = sublen*/
            auto second=tmp1->next,tmp2=second;
            tmp1->next=nullptr;        /* need to cut first's relation from all*/
            for(int i=1;i<sublen && tmp2!=nullptr && tmp2->next!=nullptr;i++){
                tmp2=tmp2->next;
            }
            /* ready to get next part(next first and next second)*/
            if(tmp2!=nullptr){
                head_tmp=tmp2->next;
                tmp2->next=nullptr;
            }else{
                /* important! */
                head_tmp=nullptr;
            }
            /* merge first and second segment */
            auto newhead=merge(first,second);
            /* IMPORTANT! head insert way!*/
            assi_node_tmp->next=newhead;
            while(assi_node_tmp->next!=nullptr){
                assi_node_tmp=assi_node_tmp->next;
            }
        }
    }
    return assi_node->next;
  }

  复杂度分析

• 时间复杂度:

• 空间复杂度:

**

判环

Floyd判圈算法(Floyd Cycle Detection Algorithm)，又称龟兔赛跑算法(Tortoise and Hare Algorithm)，是一个可以在有限状态机、迭代函数或者链表上判断是否存在环，求出该环的起点与长度的算法。

我们定义两个指针，一快一慢，慢指针每次走一步，快指针每次走两步；当两个指针从链表的同一节点开始移动时，若链表中无环，则快指针一直在慢指针前；否则，快指针会先于慢指针入环，且会在慢指针跑满环中一圈之前，追上快指针！。

slow=head,fast=head;
while(fast!=nullptr){
    if(fast->next==nullptr)
        return false;
       fast=fast->next->next;
    slow=slow->next;
    if(fast==slow)
        return true;
}
return false;

求环的起点与长度

算法

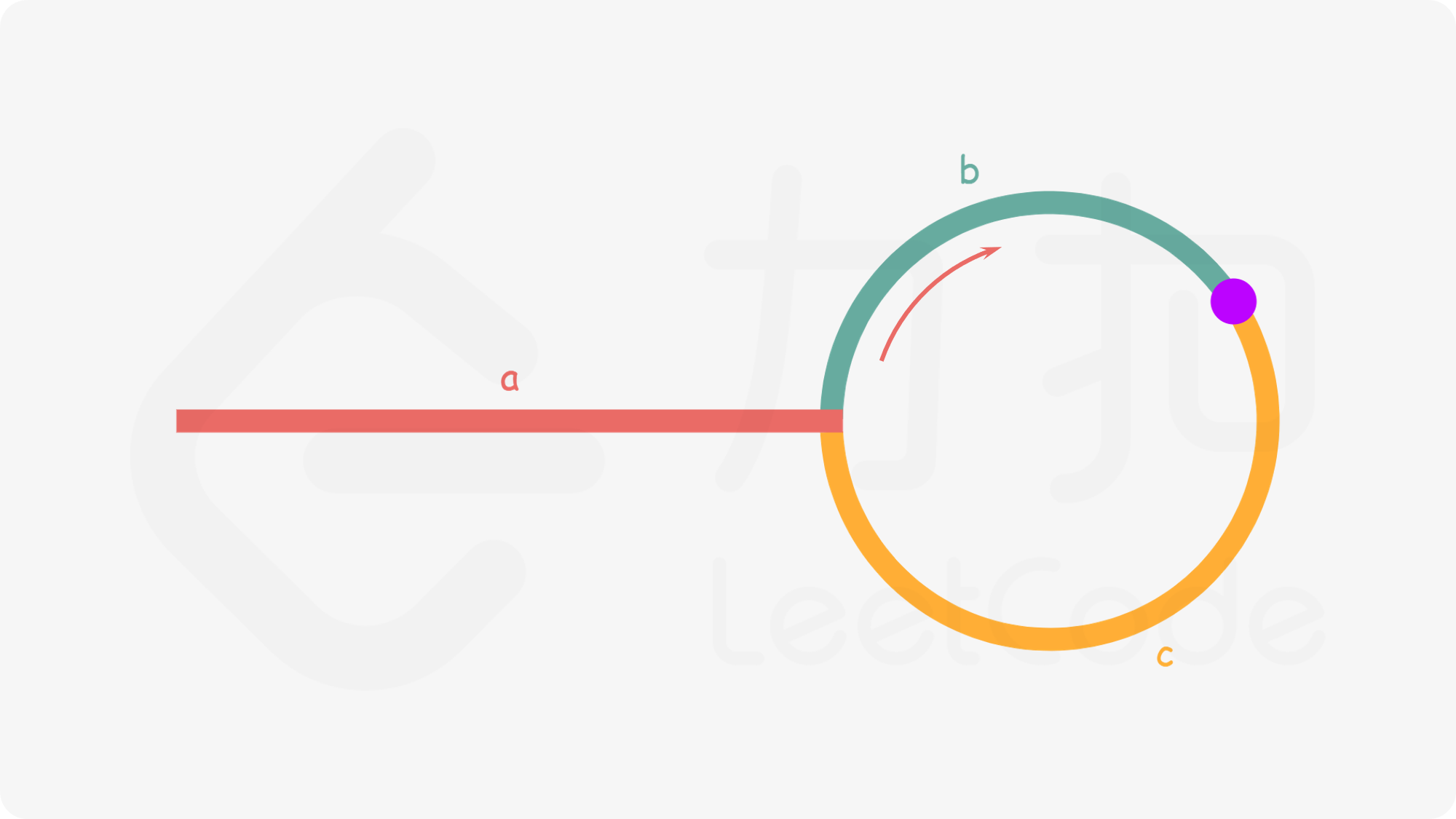
基于Floyd判圈算法， 设置快慢指针fast和slow，假设fast和slow在P点相遇，且fast已跑n圈，可得出如下结论

联立后，可得出
即环外距离等于【相遇点与环起点距离c】和【多圈环长度】之和
故当快慢指针相遇时，设置新ptr指针指向头结点。并令ptr和slow指针同步运动，直到两指针相遇时，便为环的起点。

实现

{
    auto slow=head,fast=head;
    while(fast!=nullptr){
        if(fast->next==nullptr)
            return nullptr;
        fast=fast->next->next;
        slow=slow->next;
        if(fast==slow){
            auto ptr=head;
            while(ptr!=slow){
                slow=slow->next;
                ptr=ptr->next;
            }
            return ptr;
        }
    }
    return nullptr;
 }

复杂度分析

• 时间复杂度:
• 空间复杂度: