一般方法：有一个随机数发生器（骰子）【0，k】均匀产生【a,b】

1. 将发生器生成数字-1
2. 进行两次或多次随机数生成，组成k进制数
3. 将k进制数转为10进制数
4. 需要时，去除尾部部分数，其余数概率不变
5. 对得到10进制数取余，得到【a-1,b-1】数据
6. 【a-1,b-1】数据+1获得源数据

rand7()均匀得到1-10

算法1——7进制数

分析：rand7产生1-7是等概率的；故采用7进制数方法即可

1. 将发生器数字-1
2. 抽取两次，并将其转为7进制
3. 将7进制数转为10进制，并舍去（40-48），留0-39
4. 对剩余数据取余（10）

   int GetOneToTen(){
    int x=0;
    while((x=(rand7()-1)*7+(rand7()-1))>=40);
    return x%10+1;
   }

   算法2——二进制获取0-7

   1-10的二进制表示如下： 0001 0010 …… 1010 故通过rand7()等概率获取上述二进制表示，便可实现均匀获取1-10；

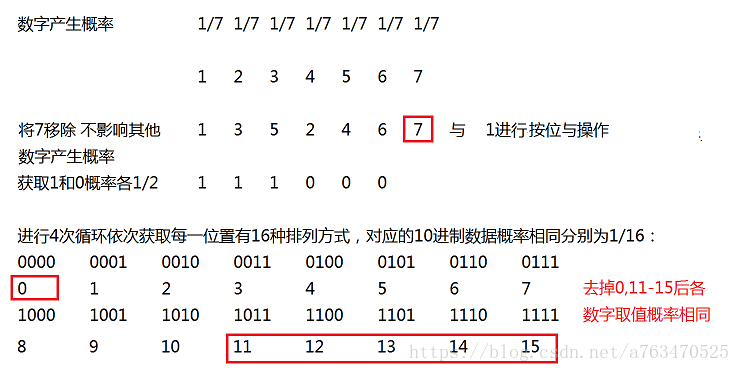
1. 移除7，获得等概率的奇偶数，与1后，获得等概率的0和1
2. 进行4次循环，获得四位二进制数，其范围为（0-15），由于均为等概率，故删除0，11-15即可

   int getBit(){
    int x=0;
    while((x=rand7())==7);
    return x&1;
   }
   int getOneToTen(){
    int x;
    do{
        x=0;
        for(int i=0;i<4;i++){
            x= x<<1 | getBit();
        }
    }(x<=0 || x>10);
    return x;
   }