84.柱状图中最大的矩形——hard-单调栈

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

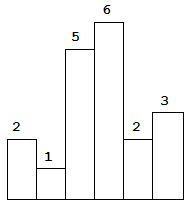
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

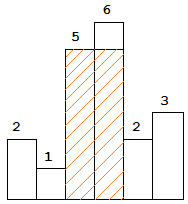
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram

思路：

栈中存放了 j 值。从栈底到栈顶，j 的值严格单调递增，同时对应的高度值也严格单调递增； 当我们枚举到第 ii 根柱子时，我们从栈顶不断地移除 height[j]≥height[i] 的 j 值。在移除完毕后，栈顶的 j 值就一定满足 height[j]<height[i] ，此时 j 就是 i 左侧且最近的小于其高度的柱子。 这里会有一种特殊情况。如果我们移除了栈中所有的 j 值，那就说明 i 左侧所有柱子的高度都大于 height[i]，那么我们可以认为 i 左侧且最近的小于其高度的柱子在位置 j=−1，它是一根「虚拟」的、高度无限低的柱子。这样的定义不会对我们的答案产生任何的影响，我们也称这根「虚拟」的柱子为「哨兵」。 我们再将 i 放入栈顶。 ——leetcode

复杂度分析:
时间复杂度O(n)
空间复杂度O(n)

var largestRectangleArea = function(heights) {
    let maxStack=[]
    heights=[0,...heights,0]
    let maxArea=0;
    for(let i=0;i<heights.length;i++){
        while(heights[i]<heights[maxStack[maxStack.length-1]]){
            let tmp=maxStack.pop()
            maxArea=Math.max(maxArea,heights[tmp]*(i-maxStack[maxStack.length-1]-1))
        }
        maxStack.push(i)
    }
    return maxArea
};