51.N皇后——hard-回溯

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

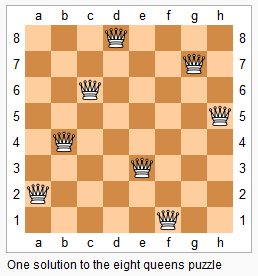
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/n-queens

思路：
N皇后是一个特别经典的回溯问题，每个皇后不能处于同一条横行(row1 == row2)、纵行(col1==col2 )、或斜线上( row1+col1==row2+col2 || row1-col1 ==row2-col2 ) 。所以可以用三个集合分别保存col、row+col、row-col，对row进行循环，每次放置皇后时判断其是否在三个集合中，如果都不在，当前位置则可以放置皇后。

复杂度分析：
时间复杂度O(N!)
空间复杂度O(N)

var solveNQueens = function (n) {
    let ans = [];
    let board = new Array(n).fill(undefined).map(() => {
        return new Array(n).fill(".");
    });
    let cols = new Set();
    let dia1 = new Set();
    let dia2 = new Set();
    let dfs = (row) => {
        if (row === n) {
            const cur = board.slice();
            for (let i = 0; i < n; i++) {
                cur[i] = cur[i].join("");
            }
            ans.push(cur);
            return;
        }
        for (let col = 0; col < n; col++) {
            if (!cols.has(col) && !dia1.has(row + col) && !dia2.has(row - col)) {
                board[row][col] = "Q";
                cols.add(col);
                dia1.add(row + col);
                dia2.add(row - col);
                dfs(row + 1);
                board[row][col] = ".";
                cols.delete(col);
                dia1.delete(row + col);
                dia2.delete(row - col);
            }
        }
    };
    dfs(0);
    return ans;
};

**