这一小节，我们好好谈一谈，如何测试得到变频器风道不同部分的风阻特性曲线，这里肯定不是简简单单的线性元件的串并联。

1.风道测试方案

机侧和网侧，还有腔体的风阻，都是未知的，但是又不能把整个变频器切割，所以拟定了三个测试方案，如图1所示，通过这三次测试结果反推各个部分的风阻，这里有一个假定，忽略风阻的耦合特性，工程上不要100%精确，只要足够精确即可。

  • 全通测试
  • 堵死机侧测试
  • 堵死网侧测试

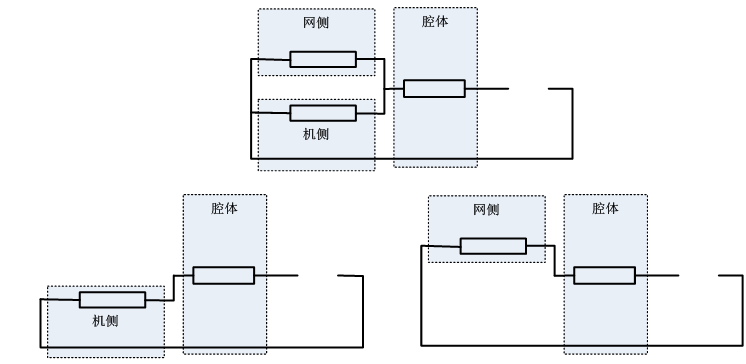
image.png
图1.风道风阻测试方案
为方便处理，做如下设定：
机侧风阻特性为P=R1(F)
网侧风阻特性为P=R2(F)
腔体风阻特性为P=R3(F)
机侧腔体串联风阻特性为P=R13(F)
网侧腔体串联风阻特性为P=R23(F)
机侧与网侧先并联然后再与腔体串联风阻特性为P=R1_23(F)
P为压强(psf)，F为流量(m^3/h)
同时作如下假设：

  • 机侧，网侧之间不存在风阻特性的耦合，
  • 腔体电阻与机侧和网侧之间不存在风阻特性的耦合

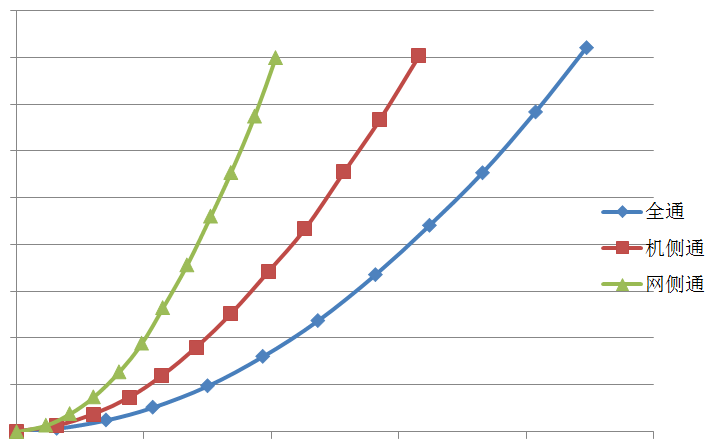
风道测试试验按照图1进行，三次测试的风阻特性测试数据如图2所示

image.png
图2.测试数据图(横轴流量，纵轴压强)

2.风道测试数据分析

利用二次函数拟合对三次测试数据拟合得到如下方程：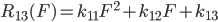
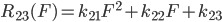
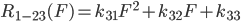
image.png
image.png
image.png
现在问题就变成已知三个环节串并联的非线性特性 ，能否求解得到三个非线性特性 ，此问题可以抽象为数学中的一个简单泛函方程问题，即已知：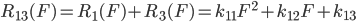
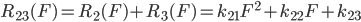
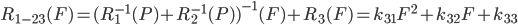
image.png
image.png
image.png
能否得到唯一的解函数 R1(F),R2(F)和R3(F)？
有关非线性泛函求解，经过查阅文献，尚未找到合适的解析解方法，工程计算上多是采用迭代优化的方式进行求解。
本文采用优化算法对泛函方程求解，根据常识知识，当P为0，F为0，所以对函数形式假设简化为为如下形式: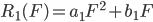
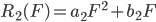
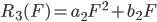
image.png
image.png
image.png
需要找到合适的 an和bn，求解的目标是使得R13(F)，R23(F)，R1_23(F)的估计值与实测曲线误差最小，这里选取误差平方和作为优化目标。
这样这个泛函方程的求解就可以表达为一个单目标的优化问题，优化向量空间为6维，即上面方程中的六个参数。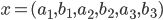
image.png
最终选用粒子群优化方法，得到的优化拟合结果如图2所示。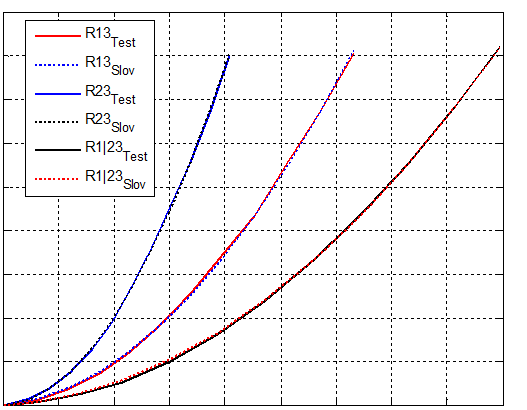
image.png
图2.拟合对比图(横轴流量，纵轴压强)
至此我们得到网侧通道，机侧通道和腔体的风阻特性曲线，如图3所示。

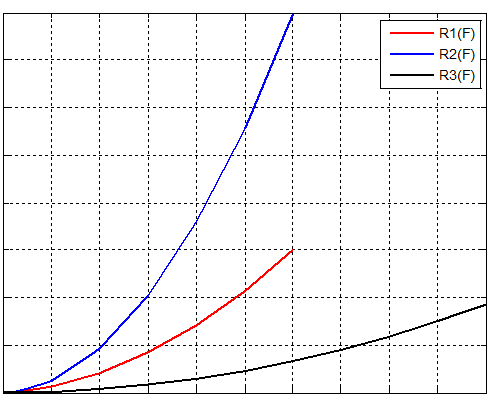
image.png
图3机侧，网侧和腔体风阻特性曲线(横轴流量，纵轴压强)

结论：

  • 风道的压强与流量关系呈二次函数形式，即P=aF^2+bF
  • 当机侧全通，网侧全通，或者机网侧全通，任何情况下腔体风阻均不可忽略。