如果我们直接对浮点数进行加减乘除运算,输出的结果可能和我们预期的很不一样。因为计算机是以二进制存储数值的,浮点数也不例外,Java 采用了 IEEE 754 标准实现浮点数的表达和运算。对于计算机而言,0.1 是无法精确表达的,这是浮点数计算造成精度损失的根源。
因此在浮点数需要精确表达和运算的场景下,一定要使用 BigDecimal 类型,BigDecimal 可以表示一个任意大小且精度完全准确的浮点数,用 scale 表示小数位数。
public class BigDecimal extends Number implements Comparable<BigDecimal> {private final BigInteger intVal;private final int scale; // 表示此BigDecimal的小数位数,包含最后的0,如1.101的小数位数为3private transient int precision; // 精度,表示有效数字的长度,如1.101的精度为4private transient String stringCache; // 用于存储规范的字符串表示形式(如果已计算),toString会使用private final transient long intCompact; // 如果此BigDecimal的有效位数的绝对值小于等于Long.MAX_VALUE,则可以将该值存储在此字段中并在计算中使用......}
构造方法
使用 BigDecimal 表示和计算浮点数,请务必使用字符序列的构造方法来初始化 BigDecimal。虽然 BigDecimal 提供了多种不同的构造函数,但盲目使用某些构造函数会存在精度缺失的问题,具体如下:
基本构造方法:
/*** 将BigDecimal的字符数组表示形式转换成BigDecimal* offset表示从in数组的第几个元素开始,len表示获取字符的总长度* MathContext封装了描述数字运算符的某些规则的上下文设置,包括四舍五入的精度位数和四舍五入的模式*/public BigDecimal(char[] in)public BigDecimal(char[] in, int offset, int len)public BigDecimal(char[] in, MathContext mc)public BigDecimal(char[] in, int offset, int len, MathContext mc)/*** 内部调用了char数组的逻辑*/public BigDecimal(String val)public BigDecimal(String val, MathContext mc)/*** 将double转换为BigDecimal,返回的BigDecimal是double的二进制浮点值的精确十进制表示形式* 此构造函数的结果可能无法预测,因为类似0.1这种的小数不能精确地表示为double,而BigDecimal(String)构造函数是完全可预测的,因此要优先使用后者* 如果必须传入double类型时,可以使用BigDecimal.valueOf(double)方法,该方法提供了精确的转换*/public BigDecimal(double val)public BigDecimal(double val, MathContext mc)/*** 将int类型转换成BigDecimal,scale被设置为0*/public BigDecimal(int val)public BigDecimal(int val, MathContext mc)
静态工厂方法:
/*** 使用Double#toString(double)方法提供的double规范字符串表示形式,将double转换为BigDecimal*/public static BigDecimal valueOf(double val)/*** 将long值转换为小数位数为零的BigDecimal*/public static BigDecimal valueOf(long val)public static BigDecimal valueOf(long unscaledVal, int scale)
注意事项:
上面提到了这几种构造方法的区别,这里还有一点要说明下,既然不推荐通过直接传入 double 类型的参数来构建 BigDecimal,那可以通过 Double#toString 方法转成字符串再构建 BigDecimal 吗?
System.out.println(new BigDecimal("4.015").multiply(new BigDecimal(Double.toString(100))));// 401.5000System.out.println(new BigDecimal("4.015").multiply(new BigDecimal("100")));// 401.500
从输出结果可以看到,虽然没有产生精度丢失的问题,但两者输出的结果却不一样,原因就在于 BigDecimal 是有 scale 和 precision 的概念,其中 scale 表示小数点右边的位数,而 precision 表示精度,也就是有效数字的长度。
通过调试可以发现,new BigDecimal(Double.toString(100)) 得到的 BigDecimal 的 scale=1、precision=4;而 new BigDecimal(“100”) 得到的 BigDecimal 的 scale=0、precision=3。对于 BigDecimal 乘法操作,返回值的 scale 是两个数的 scale 相加。所以初始化 100 的两种不同方式,导致最后结果的 scale 分别是 4 和 3。
private static void testScale() {BigDecimal bigDecimal1 = new BigDecimal("100");BigDecimal bigDecimal2 = new BigDecimal(String.valueOf(100d));BigDecimal bigDecimal3 = new BigDecimal(String.valueOf(100));BigDecimal bigDecimal4 = BigDecimal.valueOf(100d);BigDecimal bigDecimal5 = new BigDecimal(Double.toString(100));print(bigDecimal1); //scale 0 precision 3 result 401.500print(bigDecimal2); //scale 1 precision 4 result 401.5000print(bigDecimal3); //scale 0 precision 3 result 401.500print(bigDecimal4); //scale 1 precision 4 result 401.5000print(bigDecimal5); //scale 1 precision 4 result 401.5000}private static void print(BigDecimal bigDecimal) {log.info("scale {} precision {} result {}", bigDecimal.scale(), bigDecimal.precision(), bigDecimal.multiply(new BigDecimal("4.015")));}
对于浮点数的字符串形式输出和格式化,我们应该考虑显式进行,通过格式化表达式或格式化工具来明确小数位数和舍入方式。
常用方法
算术运算常用方法:
// 加法public BigDecimal add(BigDecimal augend)public BigDecimal add(BigDecimal augend, MathContext mc)// 减法public BigDecimal subtract(BigDecimal subtrahend)public BigDecimal subtract(BigDecimal subtrahend, MathContext mc)// 乘法public BigDecimal multiply(BigDecimal multiplicand)public BigDecimal multiply(BigDecimal multiplicand, MathContext mc)// 除法,scale表示商的小数位数public BigDecimal divide(BigDecimal divisor, RoundingMode roundingMode)public BigDecimal divide(BigDecimal divisor, int scale, RoundingMode roundingMode)public BigDecimal divide(BigDecimal divisor, MathContext mc)// 如果得到的商不能被精确表示,则抛出异常public BigDecimal divide(BigDecimal divisor)// 返回四舍五入的商的整数部分,MathContext主要用于限制精度位数public BigDecimal divideToIntegralValue(BigDecimal divisor)public BigDecimal divideToIntegralValue(BigDecimal divisor, MathContext mc)// 取余,即this%divisorpublic BigDecimal remainder(BigDecimal divisor)public BigDecimal remainder(BigDecimal divisor, MathContext mc)// 返回的数组包含两个BigDecimal,分别是商和余数,其中商总是整数,余数不会大于除数。我们可以利用这个方法判断两个BigDecimal是否是整数倍数public BigDecimal[] divideAndRemainder(BigDecimal divisor)public BigDecimal[] divideAndRemainder(BigDecimal divisor, MathContext mc)// 绝对值public BigDecimal abs()public BigDecimal abs(MathContext mc)// 负数public BigDecimal negate()public BigDecimal negate(MathContext mc)// 正数public BigDecimal plus()public BigDecimal plus(MathContext mc)// scale获取小数位数,precision获取精度位数public int scale()public int precision()
小数点移动运算:
// 返回等效的BigDecimal,小数点向左、右移动n位public BigDecimal movePointLeft(int n)public BigDecimal movePointRight(int n)// 可以将一个BigDecimal格式化为一个相等的,但末尾去掉了0的BigDecimalpublic BigDecimal stripTrailingZeros()
数值溢出处理:
public BigInteger toBigInteger()// 超过Integer最大值则抛出异常public BigInteger toBigIntegerExact()public int intValue()public int intValueExact()public long longValue()public long longValueExact()public float floatValue()public double doubleValue()public short shortValueExact()public byte byteValueExact()
舍入模式
1. UP
RoundingMode.UP
定义:远离零方向舍入
解释:始终对非零舍弃部分前面的数字加 1。注意,此舍入模式始终不会减少计算值的绝对值。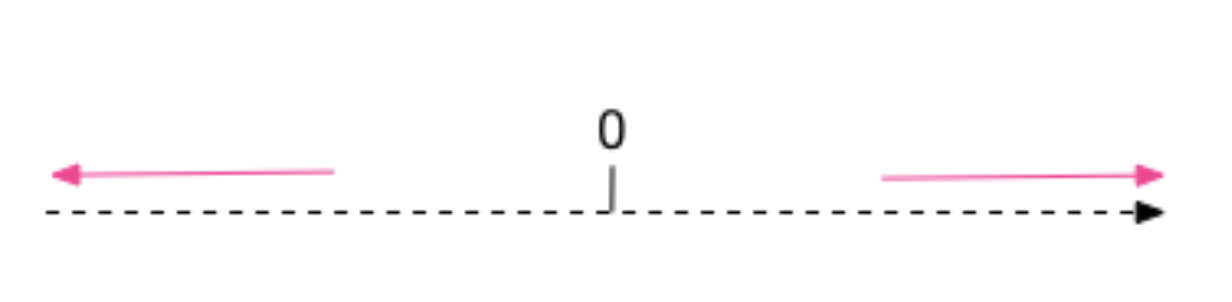
| 输入数字 | 使用 UP 舍入模式将输入数字舍入为一位数 |
|---|---|
| 5.5 | 6 |
| 2.5 | 3 |
| 1.6 | 2 |
| 1.1 | 2 |
| 1.0 | 1 |
| -1.0 | -1 |
| -1.1 | -2 |
| -1.6 | -2 |
| -2.5 | -3 |
| -5.5 | -6 |
2. DOWN
RoundingMode.DOWN
定义:向零方向舍入
解释:从不对舍弃部分前面的数字加 1(即截尾)。注意,此舍入模式始终不会增加计算值的绝对值。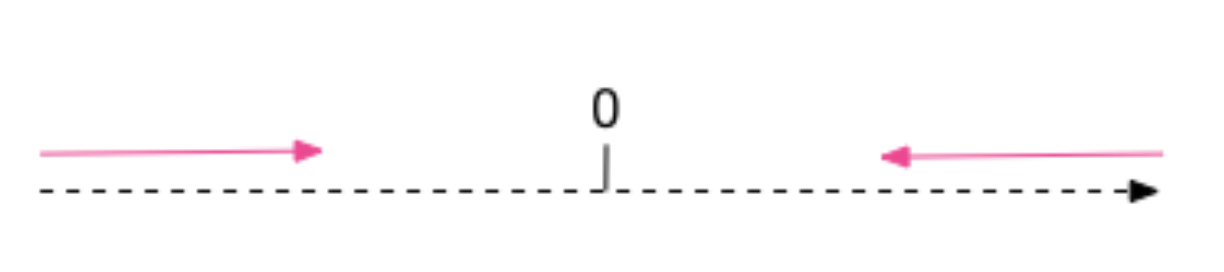
| 输入数字 | 使用 DOWN 舍入模式将输入数字舍入为一位数 |
|---|---|
| 5.5 | 5 |
| 2.5 | 2 |
| 1.6 | 1 |
| 1.1 | 1 |
| 1.0 | 1 |
| -1.0 | -1 |
| -1.1 | -1 |
| -1.6 | -1 |
| -2.5 | -2 |
| -5.5 | -5 |
3. CEILING
RoundingMode.CEILING
定义:向正无限大方向舍入
解释:如果结果为正,则舍入行为类似于 RoundingMode.UP;如果为负则类似 RoundingMode.DOWN。注意,此舍入模式始终不会减少计算值。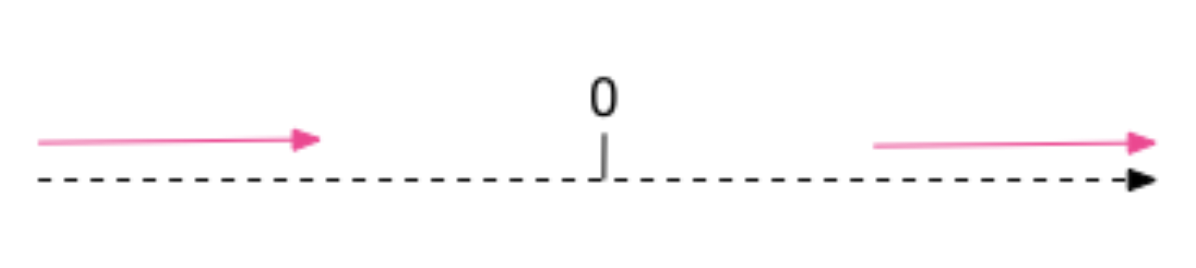
| 输入数字 | 使用 DOWN 舍入模式将输入数字舍入为一位数 |
|---|---|
| 5.5 | 6 |
| 2.5 | 3 |
| 1.6 | 2 |
| 1.1 | 2 |
| 1.0 | 1 |
| -1.0 | -1 |
| -1.1 | -1 |
| -1.6 | -1 |
| -2.5 | -2 |
| -5.5 | -5 |
4. FLOOR
RoundingMode.FLOOR
定义:向负无限大方向舍入
解释:如果结果为正,则舍入行为类似于 RoundingMode.DOWN;如果为负则类似 RoundingMode.UP。注意,此舍入模式始终不会增加计算值。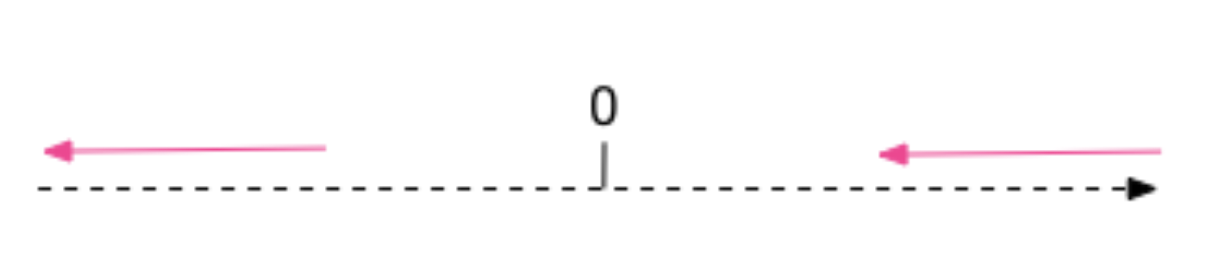
| 输入数字 | 使用 DOWN 舍入模式将输入数字舍入为一位数 |
|---|---|
| 5.5 | 6 |
| 2.5 | 3 |
| 1.6 | 2 |
| 1.1 | 2 |
| 1.0 | 1 |
| -1.0 | -1 |
| -1.1 | -1 |
| -1.6 | -1 |
| -2.5 | -2 |
| -5.5 | -5 |
5. HALF_UP
RoundingMode.HALF_UP
定义:向最接近的数字方向舍入,如果与两个相邻数字的距离相等,则向上舍入。
解释:如果被舍弃部分 >= 0.5,则舍入行为同 RoundingMode.UP;否则同 RoundingMode.DOWN。注意,此舍入模式就是通常讲的四舍五入。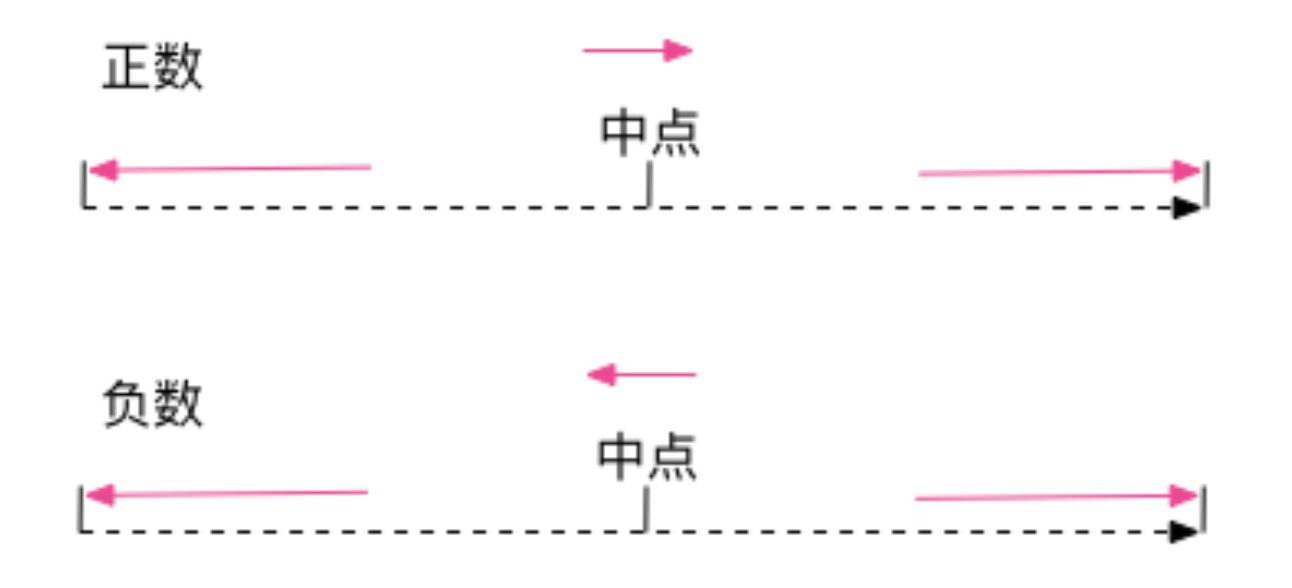
| 输入数字 | 使用 DOWN 舍入模式将输入数字舍入为一位数 |
|---|---|
| 5.5 | 6 |
| 2.5 | 3 |
| 1.6 | 2 |
| 1.1 | 1 |
| 1.0 | 1 |
| -1.0 | -1 |
| -1.1 | -1 |
| -1.6 | -2 |
| -2.5 | -3 |
| -5.5 | -6 |
6. HALF_DOWN
RoundingMode.HALF_DOWN
定义:向最接近的数字方向舍入,如果与两个相邻数字的距离相等,则向下舍入。
解释:如果被舍弃部分 > 0.5,则舍入行为同 RoundingMode.UP;否则同 RoundingMode.DOWN。注意,此舍入模式就是通常讲的五舍六入。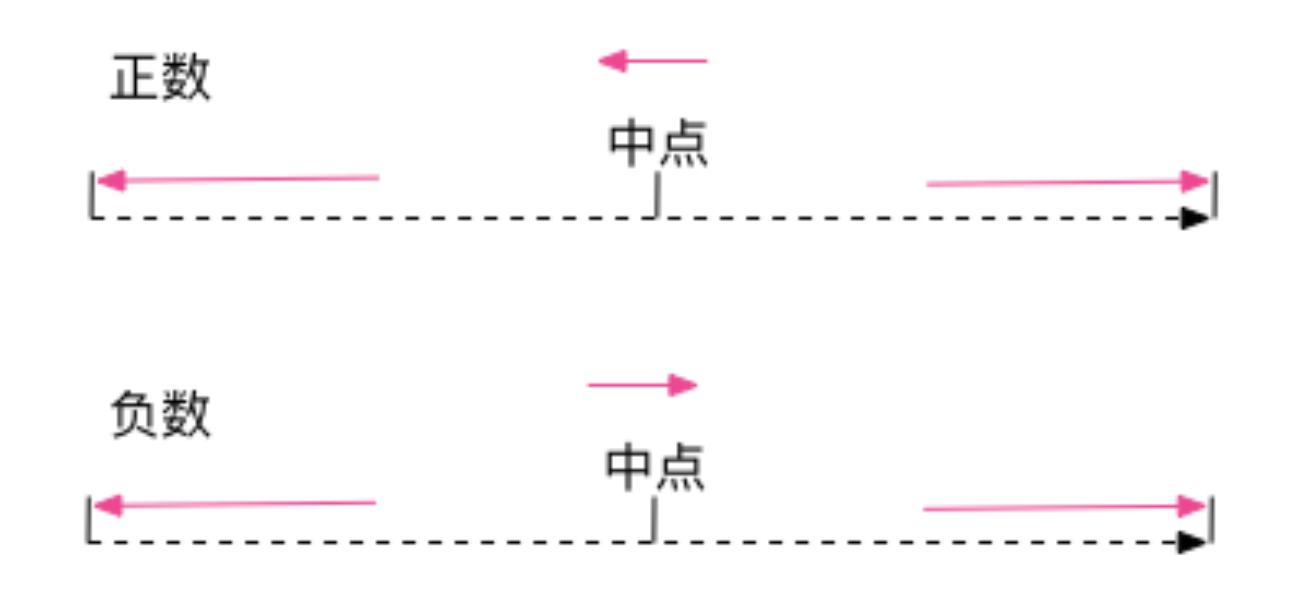
| 输入数字 | 使用 DOWN 舍入模式将输入数字舍入为一位数 |
|---|---|
| 5.5 | 5 |
| 2.5 | 2 |
| 1.6 | 2 |
| 1.1 | 1 |
| 1.0 | 1 |
| -1.0 | -1 |
| -1.1 | -1 |
| -1.6 | -2 |
| -2.5 | -2 |
| -5.5 | -5 |
7. HALF_EVEN
RoundingMode.HALF_EVEN
定义:向最接近数字方向舍入,如果与两个相邻数字的距离相等,则向相邻的偶数舍入。
解释:如果舍弃部分左边的数字为奇数,则舍入行为同 RoundingMode.HALF_UP;如果为偶数,则舍入行为同 RoundingMode.HALF_DOWN。注意,在重复进行一系列计算时,根据统计学,此舍入模式可以在统计上将累加错误减到最小。此舍入模式类似于 Java 中对 float 和 double 算法使用的舍入策略。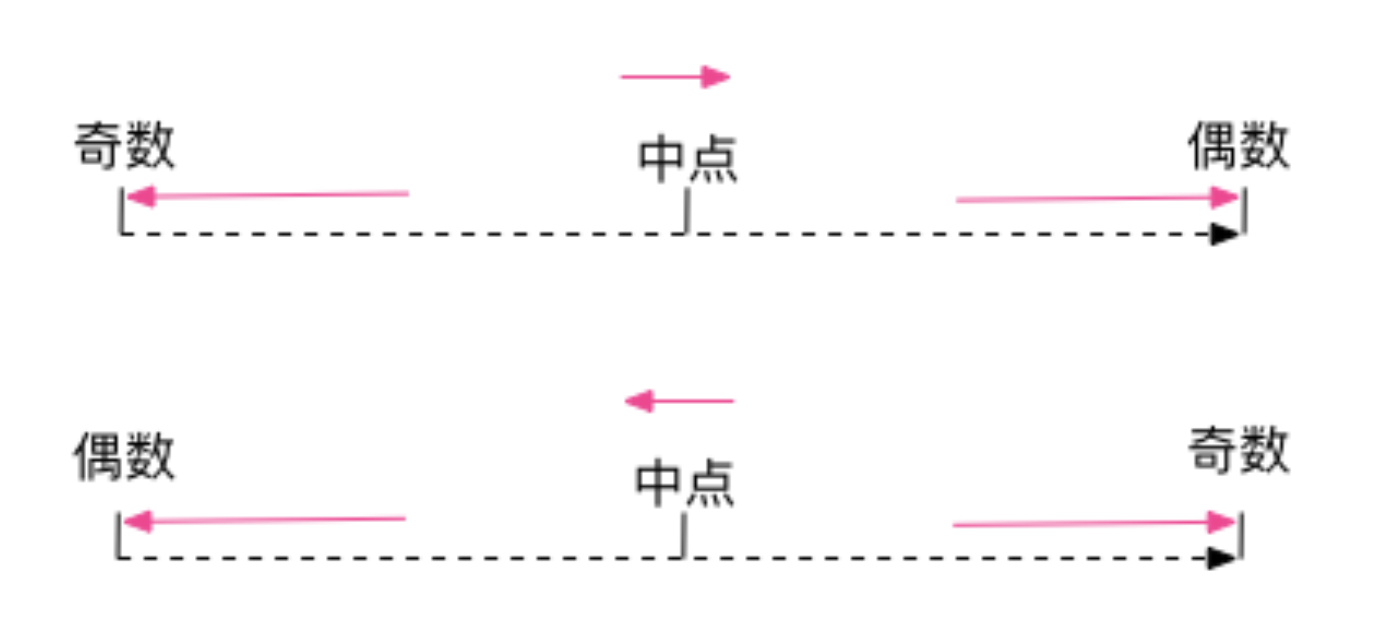
| 输入数字 | 使用 DOWN 舍入模式将输入数字舍入为一位数 |
|---|---|
| 5.5 | 6 |
| 2.5 | 2 |
| 1.6 | 2 |
| 1.1 | 1 |
| 1.0 | 1 |
| -1.0 | -1 |
| -1.1 | -1 |
| -1.6 | -2 |
| -2.5 | -2 |
| -5.5 | -6 |
8. UNNECESSARY
RoundingMode.UNNECESSARY
定义:用于断言请求的操作具有精确结果,因此不发生舍入。
解释:计算结果是精确的,不需要舍入,否则抛出 ArithmeticException。
判等操作
public int compareTo(BigDecimal val)public boolean equals(Object x)public BigDecimal min(BigDecimal val)public BigDecimal max(BigDecimal val)
- BigDecimal 的 equals 方法比较的是 BigDecimal 的 value 和 scale。
- BigDecimal 的 compareTo 方法比较的是 BigDecimal 的 value。
System.out.println(new BigDecimal("1.0").equals(new BigDecimal("1")));// falseSystem.out.println(new BigDecimal("1.0").compareTo(new BigDecimal("1")) == 0);// true
你可能会意识到 BigDecimal 的 equals 和 hashCode 方法会同时考虑 value 和 scale,如果结合 HashSet 或 HashMap 使用的话就可能会出现麻烦。比如,我们把值为 1.0 的 BigDecimal 加入 HashSet,然后判断其是否存在值为 1 的 BigDecimal,得到的结果却是 false:
Set<BigDecimal> hashSet1 = new HashSet<>();hashSet1.add(new BigDecimal("1.0"));System.out.println(hashSet1.contains(new BigDecimal("1")));//返回false
解决这个问题的办法有两个:
一是使用 TreeSet 替换 HashSet。TreeSet 内部比较元素使用的是 compareTo 方法。
二是把 BigDecimal 存入 HashSet 或 HashMap 前,先使用 stripTrailingZeros 方法去掉尾部的零,比较时也去掉尾部的 0,确保 value 相同的 BigDecimal 其 scale 也是一致的。
格式化
对于浮点数的格式化,如果使用 String.format 的话,可能得到让人摸不着头脑的结果。我们用 double 和 float 初始化两个 3.35 的浮点数,然后通过 String.format 使用 %.1f 来格式化这 2 个数字:
double num1 = 3.35;float num2 = 3.35f;System.out.println(String.format("%.1f", num1));System.out.println(String.format("%.1f", num2));
得到的结果居然是 3.4 和 3.3。这就是由精度问题和舍入方式共同导致的,因为 double 和 float 的 3.35 其实相当于 3.350xxx 和 3.349xxx。而 String.format 采用四舍五入的方式进行舍入,取 1 位小数,因此 double 的 3.350 四舍五入为 3.4,而 float 的 3.349 四舍五入为 3.3。
因此对于浮点数的格式化,可以考虑使用 DecimalFormat 来指定舍入方式,DecimalFormat 默认使用的舍入模式是 HALF_UP。如果想使用其他舍入方式来格式化字符串的话,可进行如下设置:
double num1 = 3.35;float num2 = 3.35f;DecimalFormat format = new DecimalFormat("#.##");format.setRoundingMode(RoundingMode.DOWN);System.out.println(format.format(num1)); // 3.35format.setRoundingMode(RoundingMode.DOWN);System.out.println(format.format(num2)); // 3.34
当我们把这 2 个浮点数向下舍入取 2 位小数时,输出分别是 3.35 和 3.34,还是我们之前说的浮点数无法精确存储的问题。因此,即使通过 DecimalFormat 来精确控制舍入方式,double 和 float 的问题也可能产生意想不到的结果,所以还是更建议使用 BigDecimal 来表示浮点数,并使用 setScale 指定舍入的位数和方式。
比如下面这段代码,使用 BigDecimal 来格式化数字 3.35,分别使用向下舍入和四舍五入方式取 1 位小数进行格式化:
BigDecimal num1 = new BigDecimal("3.35");BigDecimal num2 = num1.setScale(1, BigDecimal.ROUND_DOWN);System.out.println(num2);BigDecimal num3 = num1.setScale(1, BigDecimal.ROUND_HALF_UP);System.out.println(num3);
数值溢出
数值计算还要小心溢出,不管是 int 还是 long,所有的基本数值类型都有超出表达范围的可能性。比如对 Long 的最大值进行 +1 操作,会输出一个负数,因为 Long 的最大值 +1 变为了 Long 的最小值:
long l = Long.MAX_VALUE;System.out.println(l + 1); // -9223372036854775808System.out.println(l + 1 == Long.MIN_VALUE); // true
显然这是发生了溢出,而且是默默地溢出,并没有任何异常。这类问题非常容易被忽略,改进方式有下面 2 种。
方法一是,考虑使用 Math 类的 addExact、subtractExact 等 xxExact 方法进行数值运算,这些方法可以在数值溢出时主动抛出异常。
try {long l = Long.MAX_VALUE;System.out.println(Math.addExact(l, 1));} catch (Exception ex) {ex.printStackTrace();}java.lang.ArithmeticException: long overflowat java.lang.Math.addExact(Math.java:809)at org.geekbang.time.commonmistakes.numeralcalculations.demo3.CommonMistakesApplication.right2(CommonMistakesApplication.java:25)at org.geekbang.time.commonmistakes.numeralcalculations.demo3.CommonMistakesApplication.main(CommonMistakesApplication.java:13)
方法二是,使用大数类 BigInteger。BigDecimal 是处理浮点数的专家,而 BigInteger 则是对大数进行科学计算的专家。
如下代码,使用 BigInteger 对 Long 最大值进行 +1 操作;如果希望把计算结果转换一个 Long 变量的话,可以使用 BigInteger 的 longValueExact 方法,在转换出现溢出时,同样会抛出 ArithmeticException:
BigInteger i = new BigInteger(String.valueOf(Long.MAX_VALUE));System.out.println(i.add(BigInteger.ONE).toString());try {long l = i.add(BigInteger.ONE).longValueExact();} catch (Exception ex) {ex.printStackTrace();}9223372036854775808java.lang.ArithmeticException: BigInteger out of long rangeat java.math.BigInteger.longValueExact(BigInteger.java:4632)at org.geekbang.time.commonmistakes.numeralcalculations.demo3.CommonMistakesApplication.right1(CommonMistakesApplication.java:37)at org.geekbang.time.commonmistakes.numeralcalculations.demo3.CommonMistakesApplication.main(CommonMistakesApplication.java:11)
可以看到,通过 BigInteger 对 Long 的最大值加 1 一点问题都没有,当尝试把结果转换为 Long 类型时,则会提示 BigInteger out of long range。

