1. 问题背景

假设你在开发一款智能的词典软件，例如用户想查询单词fish，但不小心输入了fosh。编辑器是否能智能提示用户fish单词呢？
假设用户输入了fosh，那用户原本想输入的是fish还是fort呢？我们先在网易有道词典上做一下实验，接下来再讲一下原理和代码实现

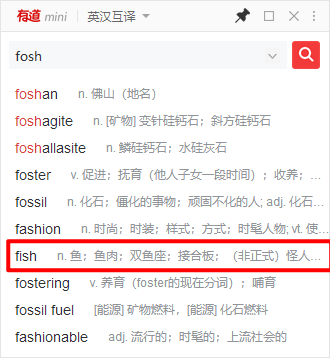
image.png
输入fosh提示fish

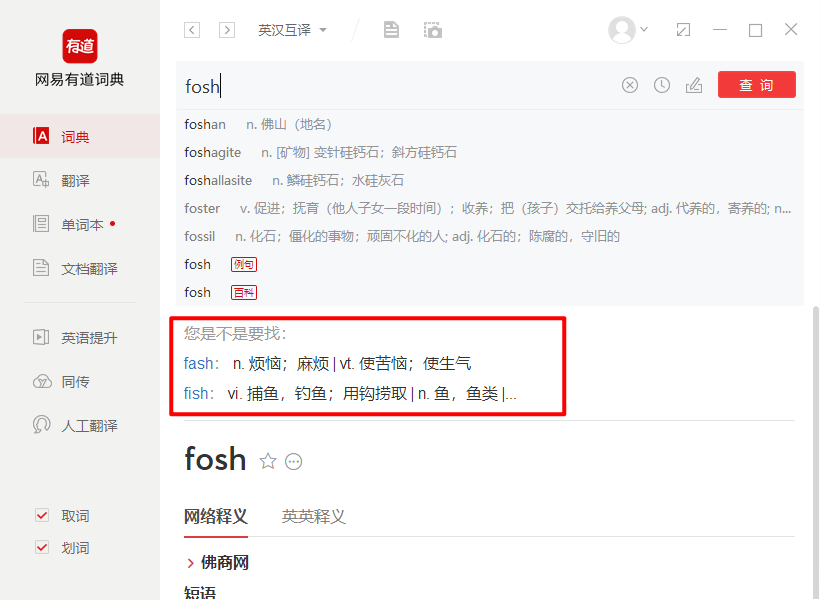
image.png
网易有道词典：输入fosh提示fish

2. 最长公共子序列问题解决原理

2.1 流程

伪代码如下

  1. if word_a[i]==word_b[j]:
  2.     cell[i][j] = cell[i-1][j-1]+1
  3. else:
  4.     cell[i][j]=max(cell[i-1][j],cell[i][j-1])

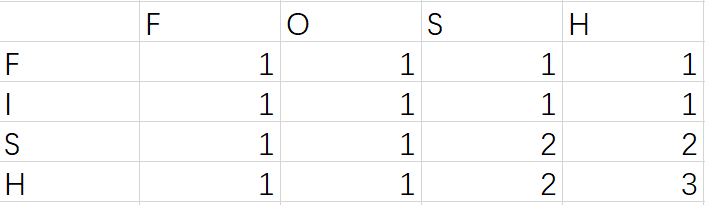
以下为表格法计算最长公共子序列可以看出，
FOSH与FORT为2
FOSH与FISH为3
所以用户更可能是想输入FISH这个单词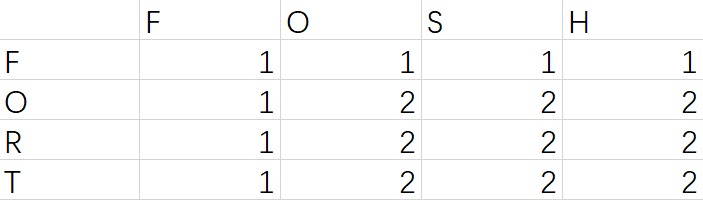
image.png
FOSH与FORT的对比

image.png
FOSH与FISH的对比

2.2 代码实现

相比学术届的MatLab，Java、JavaScript等语言在工业界更流行， 笔者经常使用JavaScript语言进行开发，所以给出JavaScript计算最长公共子序列的JavaScript实现

  1. /**
  2.  * Create a matrix
  3.  * @param {number} rows Number of rows
  4.  * @param {number} columns ANumber of columns
  5.  * @returns {Array} Matrix
  6.  */
  7. const createMatrix = (rows = 0, columns = 0) => {
  8.   const matrix = [];
  10.   for (let i = 0; i < rows; i++) {
  11.     matrix[i] = Array(columns).fill(0);
  12.   }
  14.   return matrix;
  15. };
  17. /**
  18.  * Find the longest substring
  19.  * @param {string} firstWord First word
  20.  * @param {string} secondWord Second word
  21.  * @returns {string} The longest substring
  22.  */
  23. const longestSubstring = (firstWord = "", secondWord = "") => {
  24.   const matrix = JSON.parse(
  25.     JSON.stringify(createMatrix(firstWord.length, secondWord.length))
  26.   );
  27.   let sizeSequence = 0;
  28.   let indexSequence = 0;
  30.   for (let i = 0; i < firstWord.length; i++) {
  31.     for (let j = 0; j < secondWord.length; j++) {
  32.       if (firstWord[i] === secondWord[j]) {
  33.         matrix[i][j] = (i && j) > 0 ? matrix[i - 1][j - 1] + 1 : 1;
  35.         if (matrix[i][j] >= sizeSequence) {
  36.           sizeSequence = matrix[i][j];
  37.           indexSequence = i + 1;
  38.         }
  39.       } else {
  40.         matrix[i][j] = 0;
  41.       }
  42.     }
  43.   }
  45.   return firstWord.slice(indexSequence - sizeSequence, indexSequence);
  46. };
  48. longestSubstring("vista", "hish"); // "is"
  49. longestSubstring("fish", "hish"); // "ish"
  51. /**
  52.  * Find the longest common subsequence
  53.  * @param {string} firstWord First word
  54.  * @param {string} secondWord Second word
  55.  * @returns {number} The longest common subsequence
  56.  */
  57. const longestCommonSubsequence = (firstWord = "", secondWord = "") => {
  58.   const matrix = JSON.parse(
  59.     JSON.stringify(createMatrix(firstWord.length, secondWord.length))
  60.   );
  61.   if (matrix.length === 0 || matrix[0].length === 0) return 0;
  62.   for (let i = 0; i < firstWord.length; i++) {
  63.     for (let j = 0; j < secondWord.length; j++) {
  64.       if (firstWord[i] === secondWord[j]) {
  65.         matrix[i][j] = (i && j) > 0 ? matrix[i - 1][j - 1] + 1 : 1;
  66.       } else {
  67.         matrix[i][j] = Math.max(
  68.           i > 0 ? matrix[i - 1][j] : 0,
  69.           j > 0 ? matrix[i][j - 1] : 0
  70.         );
  71.       }
  72.     }
  73.   }
  74.   return matrix[firstWord.length - 1][secondWord.length - 1];
  75. };
  77. longestCommonSubsequence("fish", "fosh"); // 3
  78. longestCommonSubsequence("fort", "fosh"); // 2

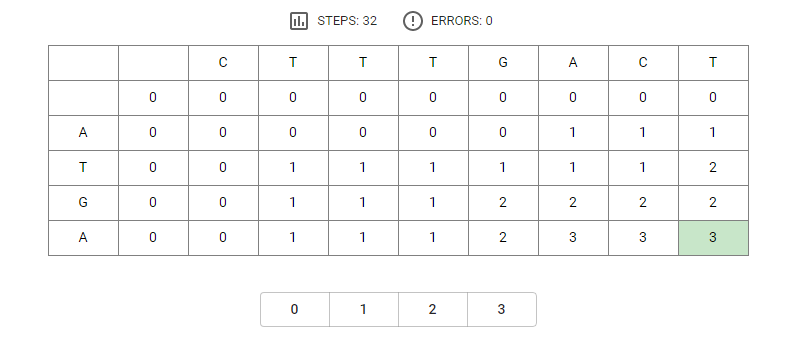
image.png
对比CTTTGACT与ATGA的公共子序列

3. 总结

在调研了过程总发现了由谷歌出品优化工具箱，并选择了一个经典的求最长公共子序列的经典问题。解决动态规划问题的思考路径如下：

  • 需要在给定约束条件下优化某种指标时，动态规划很有用
  • 问题可以分解为离散子问题时，可以使用动态规划解决
  • 每种动态规划解决方案都涉及网格
  • 单元格中的值通常就是需要优化的值
  • 每个单元格都是一个子问题，因此需要考虑如何将问题分解为子问题
  • 没有放之四海皆准的计算动态规划解决方案的公式