1. 信息量的度量-熵

信息量

信息的多少与接收者说到的信息时感到的惊讶程度相关，信息所表达的事件越不可能发生，越不可预测，信息量就越大

%7D%0A#card=math&code=I%3D%5Clog%20_a%5Cfrac%7B1%7D%7BP%5Cleft%28%20x%20%5Cright%29%7D%0A&id=dnmZP)

信息量的单位和上式中的a有关

• a=2,则信息量的单位为比特（bit）———最为常用
• a=e,则信息量的单位为奈特(nat)
• a=10,则信息量的单位为特莱(Hartley)

平均信息量

我们称平均信息量为熵，举个例子
%20%3D-%5CSigma%20%5Cleft(%20p_i%20%5Cright)%20%5Clog%20p%5Cleft(%20x_i%20%5Cright)%0A#card=math&code=H%5Cleft%28%20X%20%5Cright%29%20%3D-%5CSigma%20%5Cleft%28%20p_i%20%5Cright%29%20%5Clog%20p%5Cleft%28%20x_i%20%5Cright%29%0A&id=HYOE4)

一离散信源有0,1,2,3这4个符号组成概率分别如下

%20%3D-p_0%5Clog%20_2P%5Cleft(%20x_0%20%5Cright)%20-p_1%5Clog%20_2P%5Cleft(%20x_1%20%5Cright)%20-p_2%5Clog%20_2P%5Cleft(%20x_2%20%5Cright)%20-p_3%5Clog%20_2P%5Cleft(%20x_3%20%5Cright)%0A#card=math&code=H%5Cleft%28%20X%20%5Cright%29%20%3D-p_0%5Clog%20_2P%5Cleft%28%20x_0%20%5Cright%29%20-p_1%5Clog%20_2P%5Cleft%28%20x_1%20%5Cright%29%20-p_2%5Clog%20_2P%5Cleft%28%20x_2%20%5Cright%29%20-p_3%5Clog%20_2P%5Cleft%28%20x_3%20%5Cright%29%0A&id=ldQ6r)

%20%3D-0.375%5Clog%20_20.375-0.25%5Clog%20_20.25-0.25%5Clog%20_20.25-0.125%5Clog%20_20.125%3D1.90564%0A#card=math&code=H%5Cleft%28%20X%20%5Cright%29%20%3D-0.375%5Clog%20_20.375-0.25%5Clog%20_20.25-0.25%5Clog%20_20.25-0.125%5Clog%20_20.125%3D1.90564%0A&id=wTlQu)

MSE Loss

Mean Squared Error
均方误差损失也是一种比较常见的损失函数，其定义为：
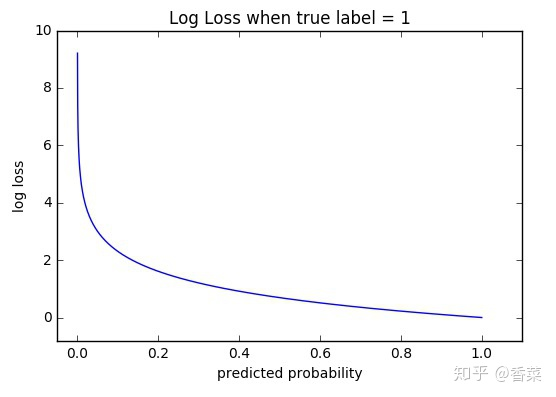
我们发现，MSE能够判断出来模型2优于模型1，那为什么不采样这种损失函数呢？主要原因是在分类问题中，使用sigmoid/softmx得到概率，配合MSE损失函数时，采用梯度下降法进行学习时，会出现模型一开始训练时，学习速率非常慢的情况（MSE损失函数）。

3. 交叉熵

以手写体数字识别为例为来生动的演示交叉熵

%20%3D%5Cunderset%7Bx%7D%7B%5CSigma%7Dp%5Cleft(%20x%20%5Cright)%20%5Clog%20%5Cleft(%20%5Cfrac%7B1%7D%7Bq%5Cleft(%20x%20%5Cright)%7D%20%5Cright)%0A#card=math&code=H%5Cleft%28%20p%2Cq%20%5Cright%29%20%3D%5Cunderset%7Bx%7D%7B%5CSigma%7Dp%5Cleft%28%20x%20%5Cright%29%20%5Clog%20%5Cleft%28%20%5Cfrac%7B1%7D%7Bq%5Cleft%28%20x%20%5Cright%29%7D%20%5Cright%29%0A&id=WxqY8)

%20%5C%2C%5C%2C%20label%5C%2C%5C%2C%3D%5C%2C%5C%2C%5Cleft%5B%20%5Cbegin%7Barray%7D%7Bc%7D%0A%091%5C%5C%0A%090%5C%5C%0A%090%5C%5C%0A%090%5C%5C%0A%5Cend%7Barray%7D%20%5Cright%5D%20%5C%2C%5C%2Cpredicate%3D%5Cleft%5B%20%5Cbegin%7Barray%7D%7Bc%7D%0A%090.8%5C%5C%0A%090.1%5C%5C%0A%090.1%5C%5C%0A%090%5C%5C%0A%5Cend%7Barray%7D%20%5Cright%5D%20%0A%5C%5C%0A%5Cleft(%20image2%20%5Cright)%20%5C%2C%5C%2C%20label%5C%2C%5C%2C%3D%5C%2C%5C%2C%5Cleft%5B%20%5Cbegin%7Barray%7D%7Bc%7D%0A%090%5C%5C%0A%090%5C%5C%0A%090%5C%5C%0A%091%5C%5C%0A%5Cend%7Barray%7D%20%5Cright%5D%20%5C%2C%5C%2Cpredicate%3D%5Cleft%5B%20%5Cbegin%7Barray%7D%7Bc%7D%0A%090.7%5C%5C%0A%090.1%5C%5C%0A%090.1%5C%5C%0A%090.1%5C%5C%0A%5Cend%7Barray%7D%20%5Cright%5D%0A#card=math&code=%5Cleft%28%20image0%20%5Cright%29%20%5C%2C%5C%2C%20label%5C%2C%5C%2C%3D%5C%2C%5C%2C%5Cleft%5B%20%5Cbegin%7Barray%7D%7Bc%7D%0A%091%5C%5C%0A%090%5C%5C%0A%090%5C%5C%0A%090%5C%5C%0A%5Cend%7Barray%7D%20%5Cright%5D%20%5C%2C%5C%2Cpredicate%3D%5Cleft%5B%20%5Cbegin%7Barray%7D%7Bc%7D%0A%090.8%5C%5C%0A%090.1%5C%5C%0A%090.1%5C%5C%0A%090%5C%5C%0A%5Cend%7Barray%7D%20%5Cright%5D%20%0A%5C%5C%0A%5Cleft%28%20image2%20%5Cright%29%20%5C%2C%5C%2C%20label%5C%2C%5C%2C%3D%5C%2C%5C%2C%5Cleft%5B%20%5Cbegin%7Barray%7D%7Bc%7D%0A%090%5C%5C%0A%090%5C%5C%0A%090%5C%5C%0A%091%5C%5C%0A%5Cend%7Barray%7D%20%5Cright%5D%20%5C%2C%5C%2Cpredicate%3D%5Cleft%5B%20%5Cbegin%7Barray%7D%7Bc%7D%0A%090.7%5C%5C%0A%090.1%5C%5C%0A%090.1%5C%5C%0A%090.1%5C%5C%0A%5Cend%7Barray%7D%20%5Cright%5D%0A&id=WRaMD)

%20%3D-1%5Clog%20_20.8-1%5Clog%20_20.1%0A#card=math&code=H%5Cleft%28%20p%2Cq%20%5Cright%29%20%3D-1%5Clog%20_20.8-1%5Clog%20_20.1%0A&id=Kj65c)

交叉熵函数性质

可以看出，该函数是凸函数，求导时能够得到全局最优值。

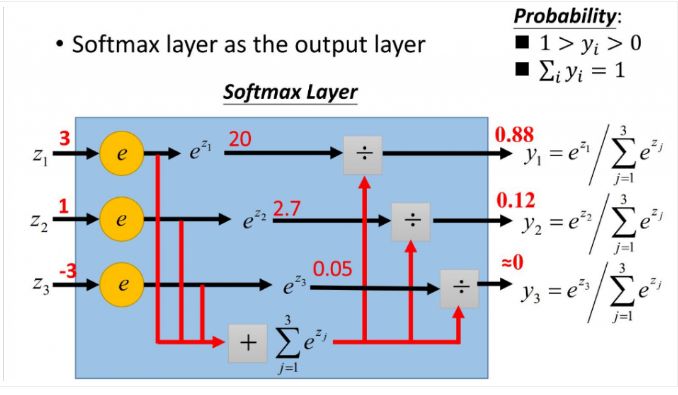
4. softmax

softmax的作用是把一组数据映射到 0-1 范围之内，且和为1

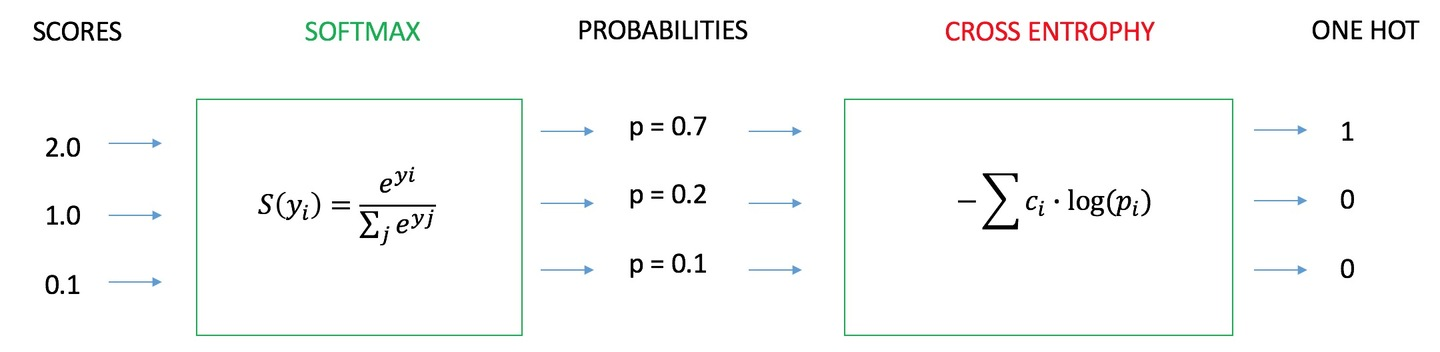
5. softmax输出作为交叉熵的输入

联合本文的第2部分和第3部分，softmax层的输出概率向量可以作为交叉熵损失函数的输入，用在分类问题上。

%20%3D-%5Clog%20_2%5Cleft(%200.88%20%5Cright)%20%3D0.184425%0A#card=math&code=%5Cmathrm%7BH%7D%5Cleft%28%20%5Cmathrm%7Bx%7D%20%5Cright%29%20%3D-%5Clog%20_2%5Cleft%28%200.88%20%5Cright%29%20%3D0.184425%0A&id=aWYQB)

参考

损失函数｜交叉熵损失函数