本文的主要从三个方面

  • Python和JavaScript库排序函数使用技巧
  • 常见排序算法盘点
  • LeetCode相关题目刷题

    排序函数使用技巧

    在工作和研究中，大多数时候我们不需要手写一个排序函数，而是要非常熟悉排序函数的接口。

    Python自定义排序规则模板

    ```python def sort_rule(x, y): a, b = x + y, y + x if a > b: return 1 elif a < b: return -1 else: return 0

strs.sort(key = functools.cmp_to_key(sort_rule))

  1. <a name="fWljm"></a>
  2. # 常见排序算法盘点
  3. 在不同领域，排序算法的实现各有千秋。总体来看，排序算法大致可分为十类：
  5. 选泡插：选择排序、冒泡排序、插入排序<br />快归希堆：快速排序、归并排序、希尔排序、堆排序<br />桶计基：桶排序、计数排序、基数排序
  6. <a name="vof10"></a>
  7. ## 时间复杂程度O(n^2)排序算法
  8. <a name="Nr5E8"></a>
  9. ### 选择排序
  10. 选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
  12. <a name="Uoh0U"></a>
  13. #### 算法步骤
  14. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。<br />再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。<br />重复第二步，直到所有元素均排序完毕。
  15. <a name="XOLGX"></a>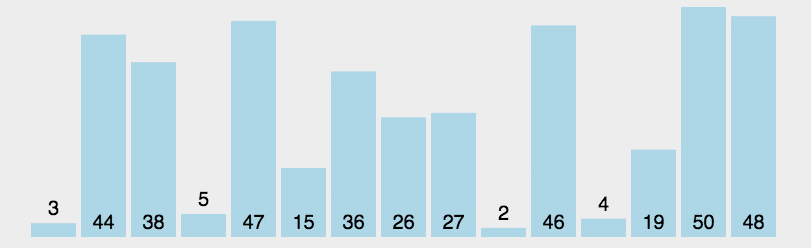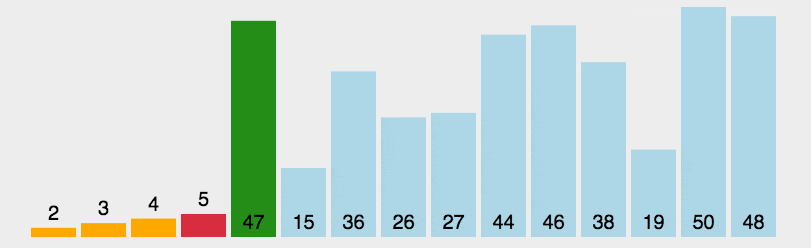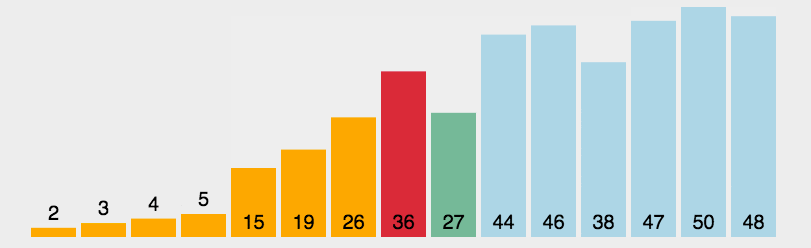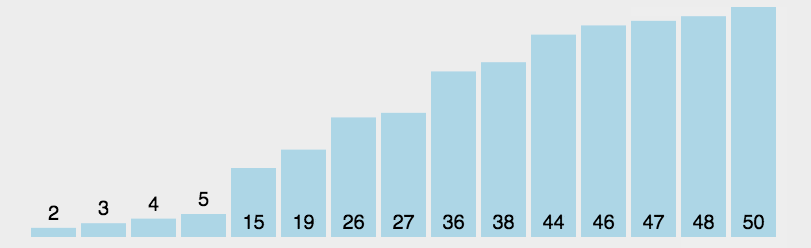
  16. #### 动图演示
  17. ![selectionSort.gif](https://cdn.nlark.com/yuque/0/2021/gif/651535/1636850020643-e635ba03-1478-4d34-bbb7-487f495508a9.gif#clientId=ufadf8cab-79fc-4&from=paste&height=248&id=u973ad67a&margin=%5Bobject%20Object%5D&name=selectionSort.gif&originHeight=248&originWidth=811&originalType=binary&ratio=1&size=470474&status=done&style=none&taskId=u7f2d82f7-f16c-4fb4-bb2c-1a254e854f7&width=811)
  18. <a name="x90Bm"></a>
  19. #### Python代码实现
  21. ```python
  22. def selectionSort(arr):
  23.   for i in range(len(arr)-1):
  24.     minIndex = i
  25.     for j in range(i+1, len(arr)):
  26.       if arr[j]<arr[minIndex]:
  27.         minIndex = j
  28.     if i!=minIndex:
  29.       arr[i],arr[minIndex] = arr[minIndex], arr[i]
  30.   return arr
  32. L1 = [3,4,5,24,5,6,34,234,534]
  33. L2 = selectionSort(L1)
  34. print(L2)

冒泡排序

算法步骤

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

动图演示

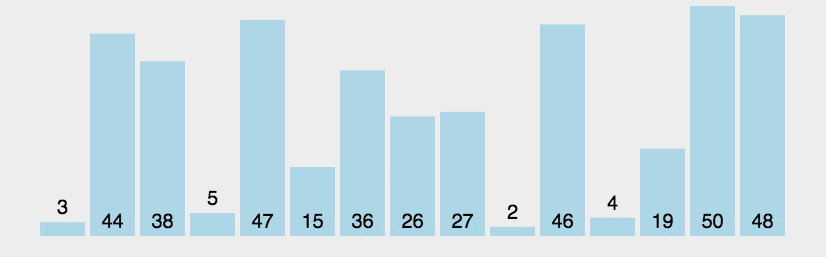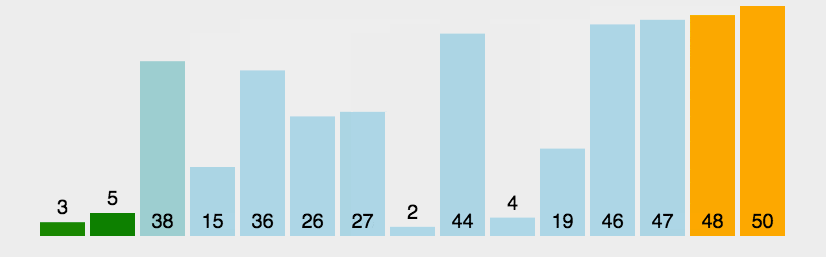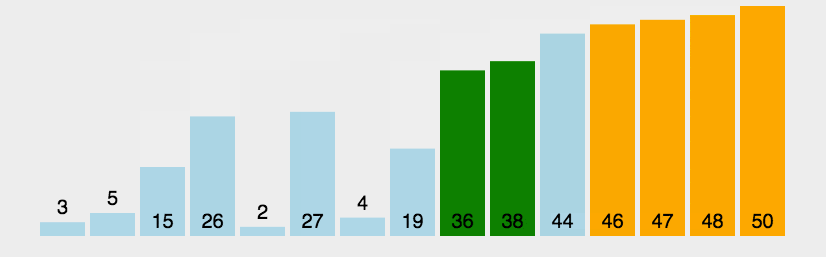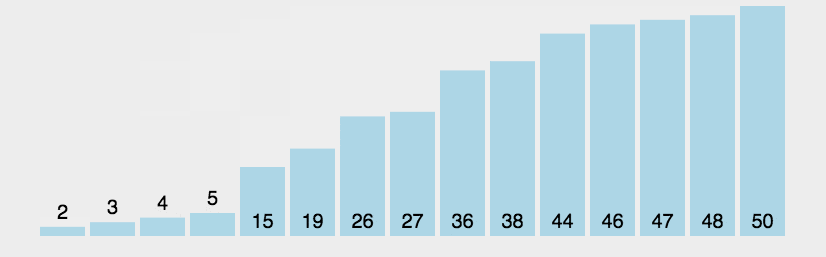
bubbleSort.gif

python代码实现

  1. def bubbleSort(arr):
  2.   for i in range(1, len(arr)):
  3.     for j in range(0, len(arr)-i):
  4.       if arr[j]>arr[j+1]:
  5.         arr[j], arr[j+1] = arr[j+1], arr[j]
  7.   return arr
  9. L1 = [3,4,5,24,5,6,34,234,534]
  10. L2 = bubbleSort(L1)
  11. print(L2)

插入排序

算法步骤

将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

动画图示

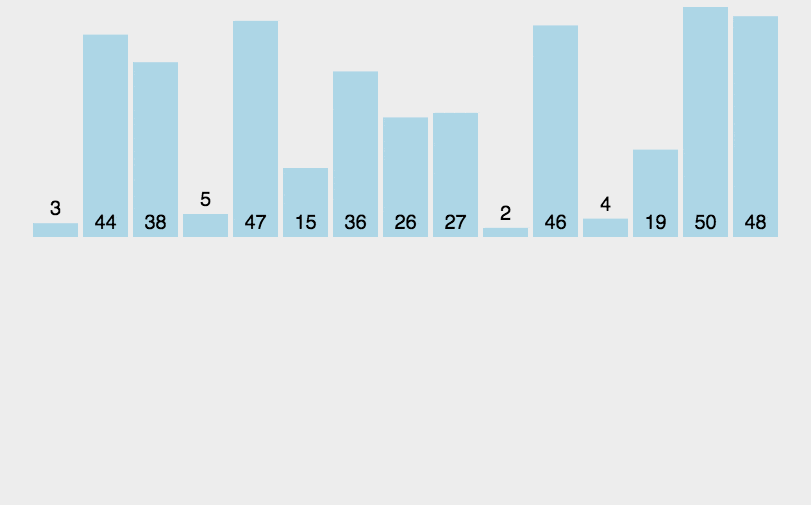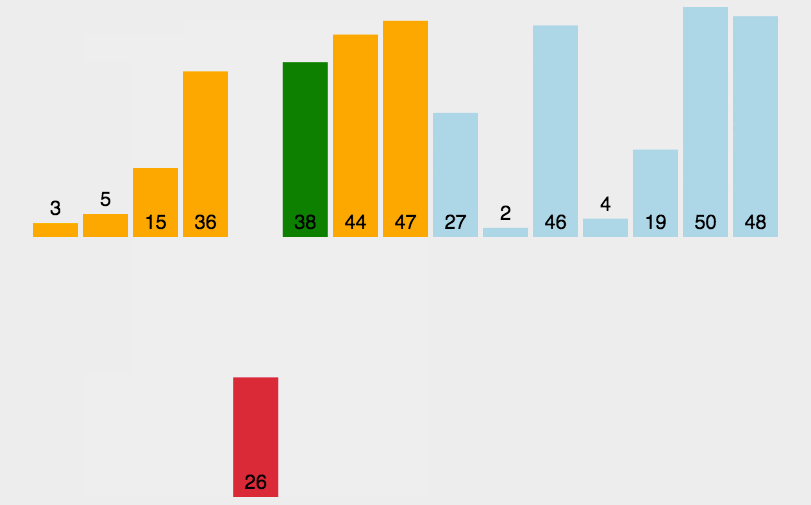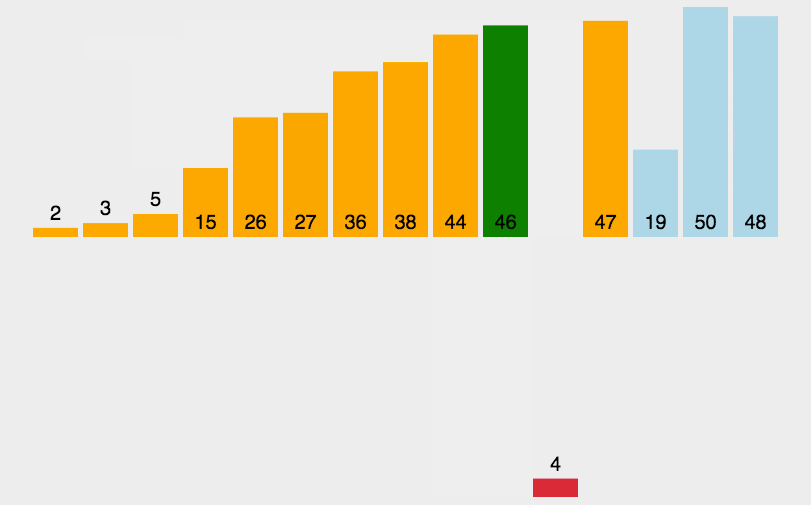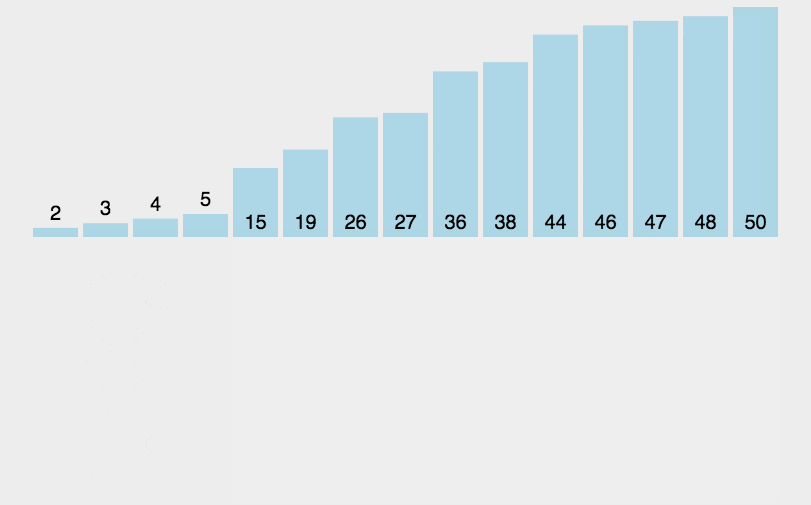
insertionSort.gif

python代码实现

  1. def insertionSort(arr):
  3.   for i in range(len(arr)):
  4.     preIndex = i - 1
  5.     current = arr[i]
  7.     while preIndex >= 0 and arr[preIndex]>current:
  8.       arr[preIndex+1] = arr[preIndex]
  9.       preIndex -=1
  11.     arr[preIndex+1] = current
  13.   return arr
  16. L1 = [3,4,5,24,5,6,34,234,534]
  17. L2 = insertionSort(L1)
  18. print(L2)

时间复杂程度O(nlogn)级排序算法

快速排序

基本思路做到理解，partition部分仍然需要深入理解。

算法步骤

  1. 从数列中挑出一个元素，称为 “基准”（pivot）;
  2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

关于基准(pivot)的选择

  • 选择第一个元素
  • 选择最后元素
  • 选择中间元素作为基础

动图示例

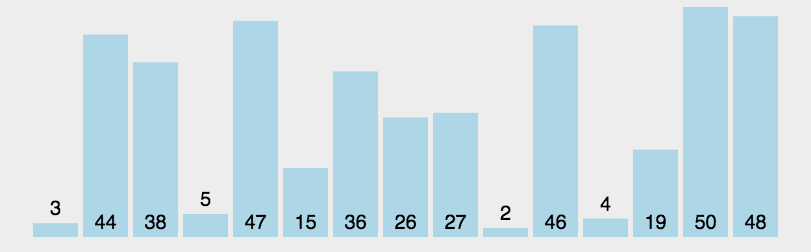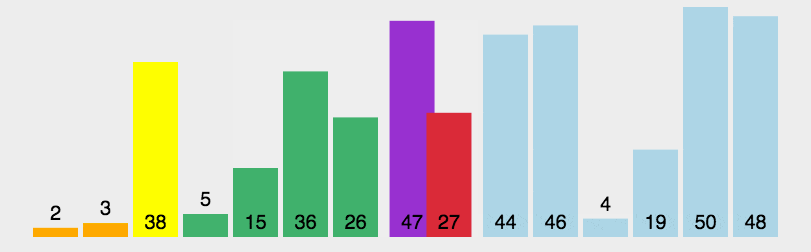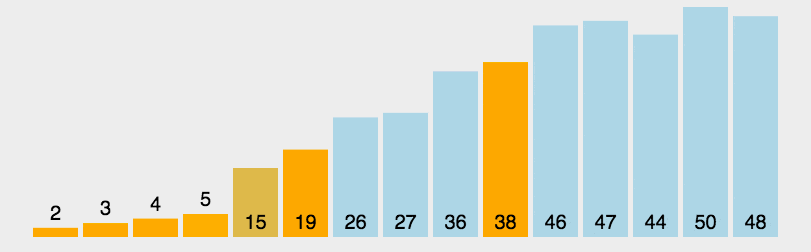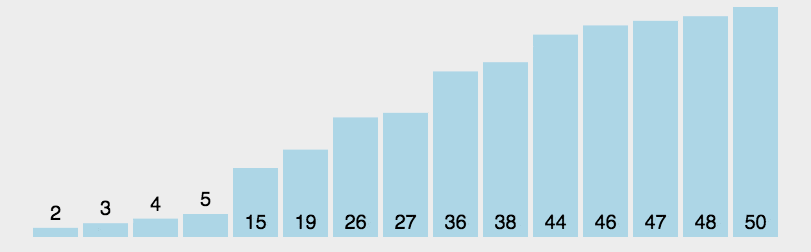
quickSort.gif

Python代码实现

以下代码中选择的基准是指定数组的第一个元素

  1. def quickSort(arr, left=None, right=None):
  2.     left = 0 if not isinstance(left,(int, float)) else left
  3.     right = len(arr)-1 if not isinstance(right,(int, float)) else right
  4.     if left < right:
  5.         partitionIndex = partition(arr, left, right)
  6.         quickSort(arr, left, partitionIndex-1)
  7.         quickSort(arr, partitionIndex+1, right)
  8.     return arr
  10. def partition(arr, left, right):
  11.     pivot = left
  12.     index = pivot+1
  13.     i = index
  14.     while  i <= right:
  15.         if arr[i] < arr[pivot]:
  16.             swap(arr, i, index)
  17.             index+=1
  18.         i+=1
  19.     swap(arr,pivot,index-1)
  20.     return index-1
  22. def swap(arr, i, j):
  23.     arr[i], arr[j] = arr[j], arr[i]

归并排序

希尔排序

堆排序

前K个大的元素，前K个小用堆排序算法解决

时间复杂度O(n)级排序算法

桶排序

计数排序

基数排序

工业级排序算法

Python排序算法剖析

JavaScript排序算法剖析

小结

排序算法 平均时间复杂程度 最好情况 最坏情况 空间复杂度 排序方式 稳定性
选择排序 O(n^2) O(n^2) O(n^2) O(1) In-place 不稳定
冒泡排序 O(n^2) O(n) O(n^2) O(1) In-place 稳定
插入排序 O(n^2) O(n) O(n^2) O(1) In-place 稳定
快速排序 O(nlogn) O(nlogn) O(n^2) O(logn) In-place 不稳定
归并排序 O(nlogn) O(nlogn) O(nlogn) O(n) Out-place 稳定
希尔排序 O(nlogn) O(nlog^2(n)) O(nlog^2(n)) O(1) In-place 不稳定
堆排序 O(nlogn) O(nlogn) O(nlogn) O(1) In-place 不稳定
桶排序 O(n+k) O(n+k) O(n^2) O(n+k) Out-place 稳定
计数排序 O(n+k) O(n+k) O(n+k) O(k) Out-place 稳定
基数排序 O(nk) O(nk) O(nk) O(n+k) Out-place 稳定

题目列表

剑指 Offer 45. 把数组排成最小的数 LCOF

  1. class Solution:
  2.     def minNumber(self, nums: List[int]) -> str:
  3.         def sort_rule(x, y):
  4.             a, b = x + y, y + x
  5.             if a > b: return 1
  6.             elif a < b: return -1
  7.             else: return 0
  9.         strs = [str(num) for num in nums]
  10.         strs.sort(key = functools.cmp_to_key(sort_rule))
  11.         return ''.join(strs)

283. 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

  1. class Solution:
  2.     def moveZeroes(self, nums: List[int]) -> None:
  3.         n = len(nums)
  4.         left = right = 0
  5.         while right < n:
  6.             if nums[right] != 0:
  7.                 nums[left], nums[right] = nums[right], nums[left]
  8.                 left += 1
  9.             right += 1

参考

本文参考以下链接进行撰写，仅作为学习用途，侵权删除

leetbook排序算法全解析
十大经典排序算法