一台计算机中,运算器只有加法运算器,没有减法运算器(减少开销)
原码,反码,补码的产生过程就是为了解决计算机做减法和引入符号位(正号和负号)的问题。
原码
用最高位表示符号位,‘1’表示负号,‘0’表示正号。其他位存放该数的二进制的绝对值。
如果我们在内存分配 4 位(bit)去存放无符号数字,是下面这样子的:
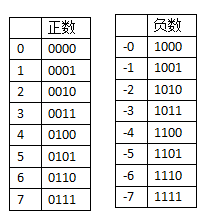
虽然出现了 +0 和 -0,但是直观易懂。
下面给出几个例子:
[0001]原 + [0010]原 = [0011]原 (1 + 2 = 3)
[1010]原 + [1101]原 = [1111]原 (-2 +(-5)= -7)
- [0000]原 + [1000]原 = [1000]原 (+0 +(-0)= -0)
[0001]原 + [1001]原 = [1010]原 (1 +(-1)= -2)
可以看出,当正数与负数相加时得出了错误结果;两个正数相加和两个负数相加,其实都是一个加法问题,只是有无符号位罢了。
而正数+负数才是真正的减法问题,于是反码出现了。
反码
正数的反码还是等于原码,负数的反码就是他的原码除符号位外按位取反。
下图给出部分正负数的二进制数反码表示法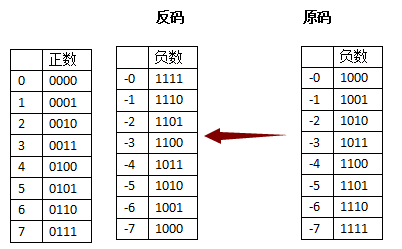
对着上图,我们再试着用反码的方式解决一下上面原码的问题:
[0001]反 + [1110]反 = [1111]反 (1+(-1)= - 0)
正数与负数相加解决了,虽然得出的结果 -0 (反码)。
但是 0 带符号是没有任何意义的,而且会有 [0000 0000]原 和 [1000 0000]原 两个编码表示 0,于是补码出现了。
补码
正数的补码等于他的原码,负数的补码等于反码+1。
下图给出带符号位四位二进制的补码表示法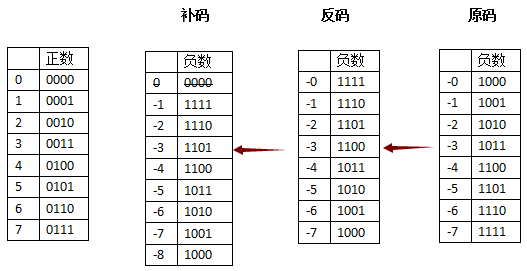
再用补码的方式解决 -0 和 +0 的问题:
[0001]补 + [1111]补 = [0000]补(1 + (-1)= 0)
在补一位 1 的时候,要丢掉最高位,这样 0 用 [0000] 表示,而以前出现问题的 -0 则不存在了。
而且还多出了一位表示 -8:
[1111]补 + [1001]补 = [1000]补(-1 + (-7)= -8)
补码原理
在生活中,假如时钟的时针停在10点钟,那么什么时候时针会停在8点钟呢。
过去隔两个小时的时候是八点钟。未来过十个小时的时候也是八点钟。
也就是:
10 - 2 = 8 而且 10 + 10 = 8
任何有限的计数系统都有一个确定的模(以上案例就使用到了),如时钟的模是12。再比如 4 位计算机的模是2^4=16(也就是四位二进制数最大容量)。
以上例子可以得出:减去一个数,是可以等同于加上另外一个正数(同余数,同余数:与减数相加正好等于模)
运用该例子,可以把减法化为加法:
0110(6)- 0010(2)= 0110(6)+1110(14)= 0100(4)
如果我们把 1110(14) 的最高位看作符号位后就是 -2 的补码,这可能也是为什么负数的符号位1 而不是 0。
然后我们再来看看为什么负数的补码的求法为什么是反码+1
- 因为负数的反码加上这个负数的绝对值正好等于 1111,再加 1,就是 1000,也就是四位二进数的模
- 而负数的补码是它的绝对值的同余数,可以通过模减去负数的绝对值,得到他的补码。

