Medium链接https://medium.com/stanford-cs224w/love-thy-neighbors-the-power-of-graph-neural-networks-dc7615e0c65f
colab连接：https://colab.research.google.com/drive/13Uzn3X1Jd4gx519vH4issp80zOJTI2ab?usp=sharing

数据集

对于本文——我们将专注于使用ogbn-arxiv数据集来探索节点分类技术。该数据集是一个有向图，表示发表在 arXiv 上的计算机科学研究论文之间的引文网络。[5]

  • 节点：每个节点代表一篇 arXiv 论文
  • 边缘：有向边缘表示一篇论文引用了另一篇论文

节点特征：图中的每个节点都有一个关联的 128 维特征向量，该向量是通过平均其标题和摘要中单词的嵌入来计算的。
数据集拆分：与随机拆分相反，数据根据论文发表日期以更现实的方式拆分。也就是说，在现实世界中，该模型将根据现有的历史论文进行训练，并用于预测新发表论文的类别。因此，训练集包含 2017 年之前发表的所有论文，验证集包含 2018 年发表的所有论文，测试集包含 2019 年以来发表的所有论文。

预测任务：节点分类

给定图中的特定节点（论文），我们的任务是预测论文属于 40 个预先确定的主题领域（即类别）中的哪一个。这些标签是由论文作者和 arXiv 版主预先确定的。这是未来的一个重要问题——随着已发表科学材料的数量持续爆炸式增长，我们将越来越需要依靠自动化方法来组织这些论文，以便于搜索和访问。

方法概述：从非 GNN 到 GNN

我们将从对传统节点分类技术（非 GNN）的高级分析开始，然后更深入地研究图神经网络（GNN）。我们将观察这些不同模型在我们的数据集上的表现，并揭示某些模型比其他模型性能更高的原因。然后，我们将讨论其他后处理方法，例如对这些模型和效果的正确和平滑。具体来说，我们将要介绍的模型如下：

  • 标签传播
  • Vanilla MLP
  • 具有 Node2Vec 功能的 MLP
  • GraphSAGE

在此处跟随我们相关的 Google Colab 笔记本来重现我们的结果！

第 I 部分：非 GNN 方法

标签传播

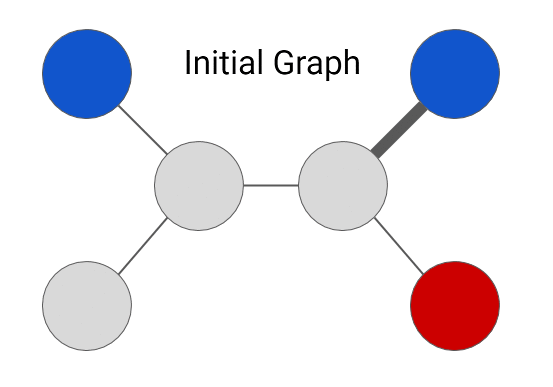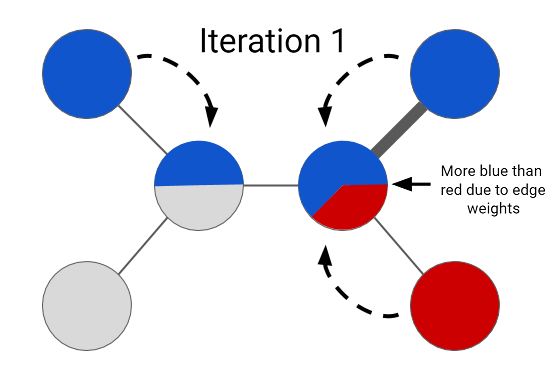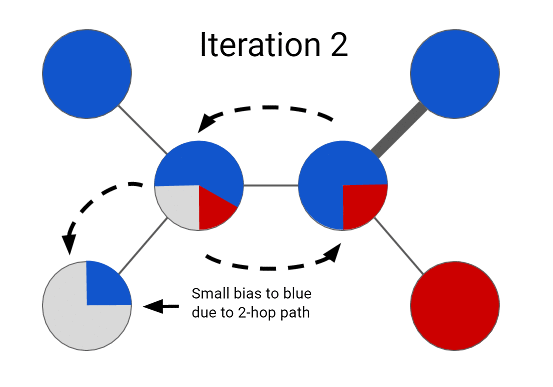
1_lQ1TQS1c4OG5tPiui_dsTQ.gif
说明标签传播直觉的 GIF（来源：CrowIntelligence.org）
不需要使用神经网络的最基本的节点级预测问题之一是标签传播算法。标签传播背后的想法是，给定图中的一些未标记节点，我们使用迭代算法通过使用概率关系分类器在数据集中传播标签来为这些未标记点分配标签。[1]。话虽如此，我们假设两个节点之间的边带有相似性的概念。这在抽象中意味着如果两个节点是连接的，那么这两个节点很可能具有相似的属性。具体来说，这种直觉延伸到我们的数据集，因为如果给定的未标记论文引用或被给定主题的许多其他标记论文引用，则这些论文很可能共享一个共同主题！
概率关系分类器背后的想法是使用概率分布在网络中传播节点标签。在这里，我们首先介绍消息传递的概念，即节点向相邻节点发送消息。对于给定的类，我们通过将所有标记节点初始化为真实值（0 或 1）并将所有未标记节点初始化为 0.5，然后以随机顺序更新所有节点，直到收敛或达到最大迭代次数。每个节点v和标签c的更新规则由下式给出：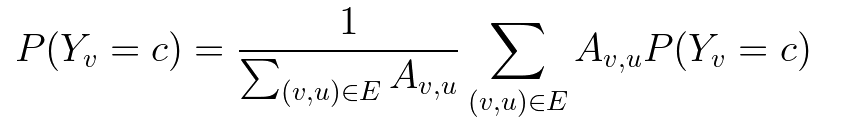
image.png
更新规则。A 是边权重矩阵，表示节点 v 和 u 在索引 (v,u) 处的边权重
在 PyG 中，这个模型实现起来非常简单，并且需要零可训练参数：

  1. from torch_geometric.nn import LabelPropagation
  3. model = LabelPropagation(num_layers=50, alpha=0.9)
  5. out = model(data.y, data.adj_t, mask=split_idx['train'])
  6. y_pred = out.argmax(dim=-1, keepdim=True)

然而，这种方法的主要限制是该模型不能使用节点特征信息。我们将通过下一个分类器克服这一挑战。

多层感知器 (MLP)

MLP 是最基本的神经网络模型架构之一，其中原始节点输入特征通过多层计算“前馈”，以产生与预测类别上的概率分布相对应的输出。

使用 Node2Vec 的 MLP

虽然 MLP 模型是一种用于节点级预测任务的神经网络方法，但它没有考虑用于分类的邻域连通性；相反，它只处理单个节点特征。在我们的数据集的上下文中，这意味着它仅根据主题/摘要的平均词嵌入对论文主题进行分类，根本不考虑引文网络——这看起来不是一种幼稚的方法吗？
我们通过引入Node2Vec来解决这个问题。Node2Vec 是一个“用于图表征学习的算法框架”。在 Node2Vec 中，我们学习了节点到低维向量空间的映射，该向量空间最大限度地保留了节点的网络邻域的可能性。换句话说，Node2Vec 在特征空间中嵌入具有相似网络邻域的节点，这样相似的节点具有相似的嵌入。[4]
Node2Vec 通过模拟有偏差的随机游走来工作，平衡网络的局部和全局视图之间的权衡。它通过定义一个返回参数p（即返回到前一个节点）和一个 in-out 参数q（直观地说，outward/DFS 和 inward/BFS 探索的“比率”）来实现，如下例所示：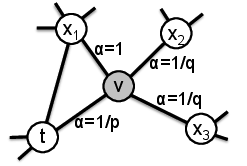
image.png
来源：SNAP Node2Vec
在 PyG 中，我们可以如下训练我们的 Node2Vec 嵌入：

  1. from torch_geometric.nn import Node2Vec
  3. nodeToVecModel = Node2Vec(edge_idx_undir, nodeToVec_args['walk_length'],
  4.                       nodeToVec_args['context_size'], nodeToVec_args['walks_per_node'],
  5.                                     sparse=True).to(device)
  7. loader = nodeToVecModel.loader(batch_size=nodeToVec_args['batch_size'], 
  8.                         shuffle=True, num_workers=4)
  10. optimizer = torch.optim.SparseAdam(list(nodeToVecModel.parameters()), 
  11.                                 lr=nodeToVec_args['lr'])
  13. nodeToVecModel.train()
  14. for epoch in range(1, nodeToVec_args['epochs'] + 1):
  15.     for i, (pos_rw, neg_rw) in enumerate(loader):
  16.         optimizer.zero_grad()
  17.         loss = nodeToVecModel.loss(pos_rw.to(device), neg_rw.to(device))
  18.         loss.backward()
  19.         optimizer.step()
  21.         if (i + 1) % nodeToVec_args['log_steps'] == 0:
  22.             print(f'Epoch: {epoch:02d}, Step: {i+1:03d}/{len(loader)}, '
  23.                   f'Loss: {loss:.4f}')

下面我们为来自 Arxiv 数据集的 1000 个随机采样节点绘制了经过训练的 Node2Vec 嵌入。我们使用 TSNE 将它们投影到二维中，并根据它们的关联类为节点着色。我们看到仅考虑邻域结构的 Node2Vec 通过相关主题显示了一些清晰的节点聚类。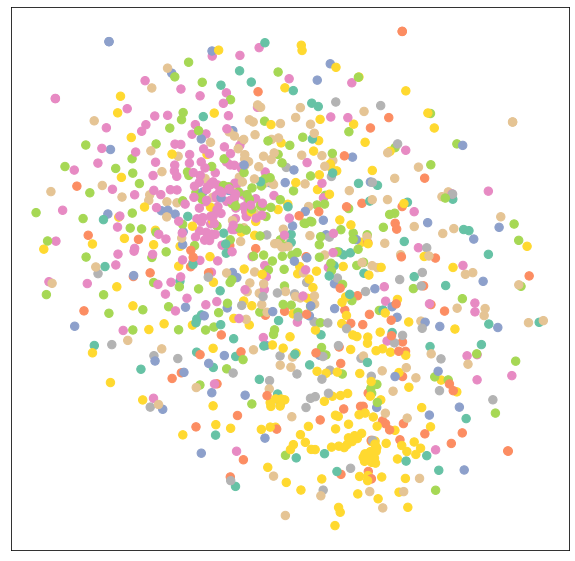
image.png
Arxiv Node2Vec 嵌入（n=1000 个节点，投影到 2D）
在这种方法中，我们将这些经过训练的节点嵌入与我们的原始节点特征连接起来，并将这些增强的特征提供给我们的原始 MLP。正如我们将在结果部分中看到的，这极大地提高了我们模型的性能！

正确平滑 (C&S)

正确和平滑（C&S）是最近的 SOTA 集体分类方法。它是一种后处理方法，旨在帮助非常简单的基础预测器通过在图上分散训练错误来提高性能。
C&S 遵循以下三步程序：

  1. 训练基础预测器
  2. 使用基本预测器来预测所有节点的软标签。
  3. 使用图结构对预测进行后处理，以获得所有节点的最终预测。

C&S 背后的想法是，我们期望基础预测器中的误差沿着图中的边呈正相关。这意味着给定节点 v，该节点上的错误会增加 v 的邻居出现类似错误的机会。因此，我们应该将这种不确定性传播到整个图上。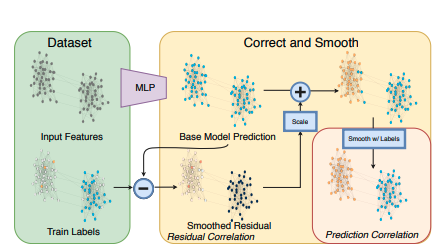
0_VaHYJ4PafPbV7QdJ.png
资料来源：“结合标签传播和简单模型优于图神经网络”
形式上，这是通过沿由下式给出的边缘扩散训练误差E来完成的：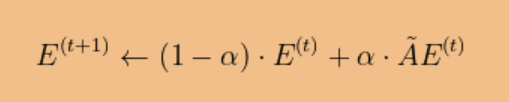
image.png
其中 A-波浪号是归一化扩散矩阵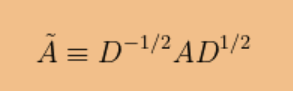
image.png
D表示度矩阵。

这可以使用有用的 PyG 库用很少的代码行来实现

  1. # y_soft are the soft labels from our base predictor
  2. adj_t = data.adj_t
  3. deg = adj_t.sum(dim=1).to(torch.float)
  4. deg_inv_sqrt = deg.pow_(-0.5)
  5. deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
  6. DAD = deg_inv_sqrt.view(-1, 1) * adj_t * deg_inv_sqrt.view(1, -1)
  7. DA = deg_inv_sqrt.view(-1, 1) * deg_inv_sqrt.view(-1, 1) * adj_t
  9. post = torch_geometric.nn.CorrectAndSmooth(num_correction_layers=50, correction_alpha=1.0,
  10.                         num_smoothing_layers=50, smoothing_alpha=0.8,
  11.                         autoscale=False, scale=20.)
  13. y_soft = post.correct(y_soft, data.y[train_idx], train_idx, DAD)
  14. y_soft = post.smooth(y_soft, data.y[train_idx], train_idx, DA)
  16. train_acc, val_acc, test_acc, _ = test(model, data.x, data.y, split_idx, evaluator, y_soft)
  17. print(f'Train: {train_acc:.4f}, Val: {val_acc:.4f}, Test: {test_acc:.4f}')

第二节：GNN 方法

我们如何将节点特征以及节点周围的邻域结构合并到模型本身的计算图中？进入图神经网络！

设计框架

我们介绍了图神经网络 (GNN) 的概念。基于 Node2Vec 的概念，GNN 是一种深度学习方法，用于学习图中节点的低维嵌入。
概括地说，GNN 设计框架有 5 个关键方面：
信息
聚合
如果目标节点仅包含来自其邻居的信息，则来自其自身嵌入的信息可能会丢失！为了解决这个问题，我们将目标节点自己的嵌入合并到聚合步骤中。实现这一点的一个简单方法是添加一个自循环。
层连通性
图增强
GNN 通过在原始输入图上构建计算图来工作。有时，为了提高性能，有必要扩充图表。有两种主要方法可以做到这一点：
特征增强：如果输入节点缺少特征，或者存在 GNN 无法建模的某些结构组件（例如，循环长度），我们可以增强节点特征来编码此信息。这类似于我们在上一节中如何使用 Node2Vec 嵌入来增强 MLP 模型！
结构增强：这方面的示例包括添加虚拟节点/边，或在图太密集时对邻居进行采样以进行消息传递。
学习目标
根据下游预测任务和我们试图优化的内容，可以选择多种损失函数公式。交叉熵 (CE)是一种标准损失函数，适用于我们选择的数据集出现的多项分类设置。

在随附的 Colab 中，我们实现了三个流行的 GCN 层供您比较和对比：

  1. 图卷积网络 (GCN)
  2. GraphSAGE
  3. 图注意网络（GAT）

下面，我们将深入研究其中一个层 GraphSAGE，以直观了解它的工作原理。

GraphSAGE

  1. from torch_geometric.nn import GCNConv, SAGEConv
  3. class SAGE(torch.nn.Module):
  4.     def __init__(self, in_channels, hidden_channels, out_channels, num_layers,
  5.                  dropout):
  6.         super(SAGE, self).__init__()
  8.         self.convs = torch.nn.ModuleList()
  9.         self.convs.append(SAGEConv(in_channels, hidden_channels))
  10.         for _ in range(num_layers - 2):
  11.             self.convs.append(SAGEConv(hidden_channels, hidden_channels))
  12.         self.convs.append(SAGEConv(hidden_channels, out_channels))
  14.         self.dropout = dropout
  16.     def reset_parameters(self):
  17.         for conv in self.convs:
  18.             conv.reset_parameters()
  20.     def forward(self, x, adj_t):
  21.         for conv in self.convs[:-1]:
  22.             x = conv(x, adj_t)
  23.             x = F.relu(x)
  24.             x = F.dropout(x, p=self.dropout, training=self.training)
  25.         x = self.convs[-1](x, adj_t)
  26.         return torch.log_softmax(x, dim=-1

我们使用我们选择的损失函数（例如，交叉熵）和优化器（例如，随机梯度下降，Adam）来训练模型，类似于其他深度学习设置

  1. from ogb.nodeproppred import Evaluator
  3. evaluator = Evaluator(name="ogbn-arxiv")
  4. optimizer = torch.optim.Adam(model.parameters(), lr=args['lr'])
  6. # Training
  7. for epoch in range(1, 1 + NUM_EPOCHS):
  8.     model.train()
  10.     optimizer.zero_grad()
  11.     out = model(data.x, data.adj_t)[train_idx]
  12.     loss = F.nll_loss(out, data.y.squeeze(1)[train_idx])
  13.     loss.backward()
  14.     optimizer.step()
  16.  # Evaluation
  17.  with torch.no_grad():
  18.   model.eval()
  19.   out = model(data.x, data.adj_t)
  20.   y_pred = out.argmax(dim=-1, keepdim=True)
  22.   train_acc = evaluator.eval({
  23.       'y_true': data.y[split_idx['train']],
  24.       'y_pred': y_pred[split_idx['train']],
  25.   })['acc']
  26.   valid_acc = evaluator.eval({
  27.       'y_true': data.y[split_idx['valid']],
  28.       'y_pred': y_pred[split_idx['valid']],
  29.   })['acc']
  30.   test_acc = evaluator.eval({
  31.       'y_true': data.y[split_idx['test']],
  32.       'y_pred': y_pred[split_idx['test']],
  33.   })['acc']

结果

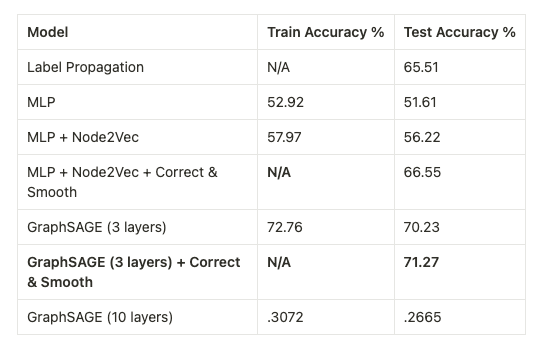
image.png
实验结果
下面我们比较了 MLP + Node2Vec 和 GraphSAGE 模型的 TSNE 投影最终嵌入。直观地说，我们看到 GraphSAGE 在物理空间中按类别分离节点方面做得更好，这证实了我们观察到的更高的分类精度。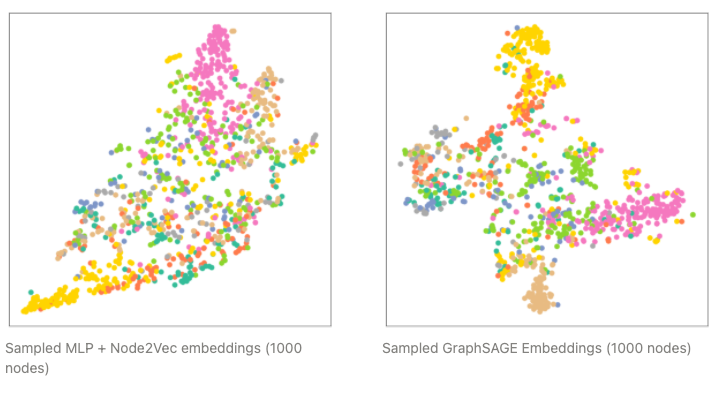
image.png

GraphSAGE 结果——深入研究

下图描述了我们的 GraphSAGE 模型超过 500 个 epoch 的学习过程：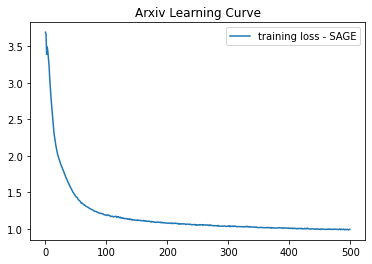
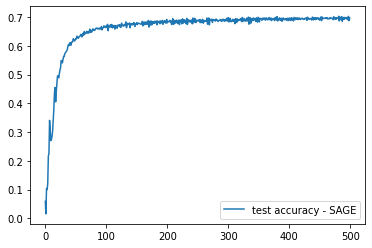
0_geHtJLTCcuOfr_dl.png0_OfnpKjuUY_Nt5GzQ.png
此外，我们制作了一个 GIF，描绘了整个训练过程中 TSNE 投影的节点嵌入，以显示节点如何随着时间的推移按类物理分离/集群，这很有意义，因为我们定义了学习目标的方式：

评估/讨论

节点和邻域

正如我们在上述模型的闪电之旅中看到的那样，仅考虑孤立的节点特征（即普通 MLP）或仅基于图结构（即标签传播）进行预测是不够的。性能最佳的模型会考虑两个节点的个体特征，以及它们的本地/全球邻域的上下文来进行预测。这就是为什么我们的最佳模型是用正确和平滑的 GraphSAGE 后处理的直觉。

C&S的力量

正确和平滑是一个强大的预处理步骤，它与模型无关。正如我们从经验上看到的，当使用 MLP 等简单模型作为基线预测器时，它的效果特别好，从而显着提高了性能。然而，即使使用像 GraphSAGE 这样的复杂 GNN 模型，我们也观察到测试准确度略有提高。直观地说，由于 GNN 设计已经通过消息传递捕获了邻域连接，因此 C&S 没有像应用于 MLP 模型后处理时那样显着改进是有道理的。

可扩展性注意事项

由于我们的数据集相对较小，并且节点之间的连接相对稀疏，因此我们能够通过全批次学习来训练我们的模型。但是，在图非常大且连接密集的环境中会发生什么，例如整个 Facebook 社交网络？为了使计算易于处理，我们引入了邻域采样的概念：在每个 GNN 层，我们最多采样H个邻域，而不是聚合来自每个相邻节点的消息：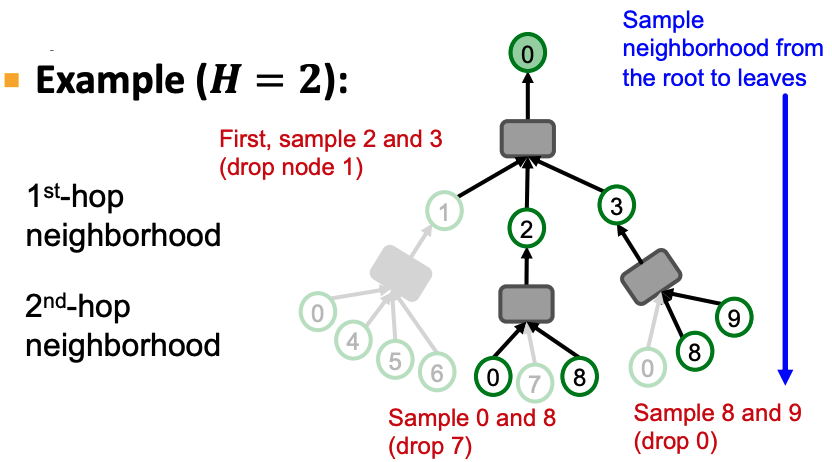
1_nGZE1gSKINPD5j5ylseb2A.png
来源：CS224W 第 17 讲（GNN 缩放）
在随附的 Colab 笔记本的末尾，我们已经实施了此解决方案，如果您发现数据集的训练过程非常缓慢/难以处理，您可以调整该解决方案。

结论

爱邻舍如同爱自己. 在这篇文章中，我们探索了解决节点分类问题的各种方法。我们从仅考虑图连接结构或孤立的节点特征的非 GNN 方法开始。然后，我们意识到我们可以通过将两者与 Node2Vec 增强相结合来实现更高的性能。从那里，我们看到了一个简单的 C&S 后处理步骤如何增强我们的结果。最后，我们介绍了最先进的 GNN 架构，展示了它们如何通过基于节点特征生成嵌入以及聚合从其周围邻域传递的消息来实现该任务的最佳性能。我们希望通过我们在 Colab 和本文中进行的实验和分析