https://colab.research.google.com/drive/14OvFnAXggxB8vM4e8vSURUp1TaKnovzX#scrollTo=eqWR0j_kIx67
官方的教程
依旧是Cora数据集。使用了MLP和GCN作为对比。

  1. # Install required packages.
  2. !pip install -q torch-scatter -f https://data.pyg.org/whl/torch-1.10.0+cu113.html
  3. !pip install -q torch-sparse -f https://data.pyg.org/whl/torch-1.10.0+cu113.html
  4. !pip install -q git+https://github.com/pyg-team/pytorch_geometric.git
  6. # Helper function for visualization.
  7. %matplotlib inline
  8. import matplotlib.pyplot as plt
  9. from sklearn.manifold import TSNE
  11. def visualize(h, color):
  12.     z = TSNE(n_components=2).fit_transform(h.detach().cpu().numpy())
  14.     plt.figure(figsize=(10,10))
  15.     plt.xticks([])
  16.     plt.yticks([])
  18.     plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
  19.     plt.show()

本教程将教您如何将图神经网络 (GNN) 应用于节点分类任务。 在这里，我们只获得了一小部分节点的真实标签，并希望推断所有剩余节点的标签（转导学习）。

为了演示，我们使用了 Cora 数据集，这是一个引用网络，其中节点代表文档。 每个节点由一个 1433 维的词袋特征向量描述。 Each node is described by a 1433-dimensional bag-of-words feature vector. 如果两个文档之间存在引用链接，则它们是连接的。 任务是推断每个文档的类别（共 7 个）。

这个数据集是由 Yang 等人首先引入的。 (2016) 作为 Planetoid 基准套件的数据集之一。 我们可以再次使用 PyTorch Geometric 通过 torch_geometric.datasets.Planetoid 轻松访问此数据集：

  1. from torch_geometric.datasets import Planetoid
  2. from torch_geometric.transforms import NormalizeFeatures
  4. dataset = Planetoid(root='data/Planetoid', name='Cora', transform=NormalizeFeatures())
  6. print()
  7. print(f'Dataset: {dataset}:')
  8. print('======================')
  9. print(f'Number of graphs: {len(dataset)}')
  10. print(f'Number of features: {dataset.num_features}')
  11. print(f'Number of classes: {dataset.num_classes}')
  13. data = dataset[0]  # Get the first graph object.
  15. print()
  16. print(data)
  17. print('===========================================================================================================')
  19. # Gather some statistics about the graph.
  20. print(f'Number of nodes: {data.num_nodes}')
  21. print(f'Number of edges: {data.num_edges}')
  22. print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')
  23. print(f'Number of training nodes: {data.train_mask.sum()}')
  24. print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}')
  25. print(f'Has isolated nodes: {data.has_isolated_nodes()}')
  26. print(f'Has self-loops: {data.has_self_loops()}')
  27. print(f'Is undirected: {data.is_undirected()}')
  1. Dataset: Cora():
  2. ======================
  3. Number of graphs: 1
  4. Number of features: 1433
  5. Number of classes: 7
  7. Data(x=[2708, 1433], edge_index=[2, 10556], y=[2708], train_mask=[2708], val_mask=[2708], test_mask=[2708])
  8. ===========================================================================================================
  9. Number of nodes: 2708
  10. Number of edges: 10556
  11. Average node degree: 3.90
  12. Number of training nodes: 140
  13. Training node label rate: 0.05
  14. Has isolated nodes: False
  15. Has self-loops: False
  16. Is undirected: True

总的来说，这个数据集与之前使用的 KarateClub 网络非常相似。 我们可以看到 Cora 网络拥有 2,708 个节点和 10,556 条边，导致平均节点度为 3.9。 为了训练这个数据集，我们得到了 140 个节点的真实类别（每个类 20 个）。 这导致训练节点标签率仅为 5%。

与 KarateClub 相比，该图包含附加属性 val_mask 和 test_mask，它们表示应使用哪些节点进行验证和测试。 此外，我们通过 transform=NormalizeFeatures()使用数据转换。 转换可用于在将输入数据输入神经网络之前对其进行修改，例如，用于规范化或数据增强。 在这里，我们对词袋输入特征向量进行行归一化。 Here, we row-normalize the bag-of-words input feature vectors.

CLASS NormalizeFeatures(attrs**: **List[str]** = **[‘x’]) Row-normalizes the attributes given in attrs to sum-up to one.

我们可以进一步看到，这个网络是无向的，不存在孤立的节点（每个文档至少有一个引用）。

a Multi-layer Perception Network (MLP)

从理论上讲，我们应该能够仅根据其内容（即词袋特征表示）来推断文档的类别，而无需考虑任何相关信息。

让我们通过构建一个仅对输入节点特征进行操作的简单 MLP（使用跨所有节点的共享权重）来验证：

  1. import torch
  2. from torch.nn import Linear
  3. import torch.nn.functional as F
  6. class MLP(torch.nn.Module):
  7.     def __init__(self, hidden_channels):
  8.         super(MLP, self).__init__()
  9.         torch.manual_seed(12345)
  10.         self.lin1 = Linear(dataset.num_features, hidden_channels)
  11.         self.lin2 = Linear(hidden_channels, dataset.num_classes)
  13.     def forward(self, x):
  14.         x = self.lin1(x)
  15.         x = x.relu()
  16.         x = F.dropout(x, p=0.5, training=self.training)
  17.         x = self.lin2(x)
  18.         return x
  20. model = MLP(hidden_channels=16)
  21. print(model)
  22. >>>
  23. MLP(
  24.   (lin1): Linear(in_features=1433, out_features=16, bias=True)
  25.   (lin2): Linear(in_features=16, out_features=7, bias=True)
  26. )

我们的 MLP 由两个线性层定义，并通过 ReLU 非线性和 dropout 增强。 在这里，我们首先将 1433 维特征向量减少到低维嵌入（hidden_channels=16），而第二个线性层充当分类器，应将每个低维节点嵌入映射到 7 个类之一。

让我们按照本教程第一部分中描述的类似过程来训练我们的简单 MLP。 我们再次利用交叉熵损失和 Adam 优化器 cross entropy loss and Adam optimizer。 这一次，我们还定义了一个测试函数来评估我们的最终模型在测试节点集上的表现（在训练过程中没有观察到哪些标签）。

  1. from IPython.display import Javascript  # Restrict height of output cell.
  2. display(Javascript('''google.colab.output.setIframeHeight(0, true, {maxHeight: 300})'''))
  4. model = MLP(hidden_channels=16)
  5. criterion = torch.nn.CrossEntropyLoss()  # Define loss criterion.
  6. optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)  # Define optimizer.
  8. def train():
  9.       model.train()
  10.       optimizer.zero_grad()  # Clear gradients.
  11.       out = model(data.x)  # Perform a single forward pass.
  12.       loss = criterion(out[data.train_mask], data.y[data.train_mask])  # Compute the loss solely based on the training nodes.
  13.       loss.backward()  # Derive gradients.
  14.       optimizer.step()  # Update parameters based on gradients.
  15.       return loss
  17. def test():
  18.       model.eval()
  19.       out = model(data.x)
  20.       pred = out.argmax(dim=1)  # Use the class with highest probability.
  21.       test_correct = pred[data.test_mask] == data.y[data.test_mask]  # Check against ground-truth labels.
  22.       test_acc = int(test_correct.sum()) / int(data.test_mask.sum())  # Derive ratio of correct predictions.
  23.       return test_acc
  25. for epoch in range(1, 201):
  26.     loss = train()
  27.     print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')

训练模型后，我们可以调用测试函数来查看我们的模型在看不见的标签上的表现如何。 在这里，我们对模型的准确性感兴趣，即正确分类节点的比率：

  1. test_acc = test()
  2. print(f'Test Accuracy: {test_acc:.4f}')
  3. >>>
  4. Test Accuracy: 0.5900

可以看出，我们的 MLP 表现相当糟糕，测试准确率只有 59% 左右。
但是为什么 MLP 的表现没有更好呢？
主要原因是该模型由于只有 少量的训练节点而遭受严重的过度拟合，因此对看不见的节点表示的泛化能力很差。

它也没有将一个重要的偏差纳入模型：被引论文很可能与文档的类别相关。
这正是图神经网络发挥作用的地方，可以帮助提高我们模型的性能。

GCN Graph Neural Network

image.png
PyG03-Node Classification with Graph Neural Networks - 图2
其中 W(ℓ+1) 表示形状为 [num_output_features, num_input_features]的可训练权重矩阵，cw,v 表示每个边的固定归一化系数。
相反，单个线性层被定义为PyG03-Node Classification with Graph Neural Networks - 图3，没有使用相邻节点信息。

  1. from torch_geometric.nn import GCNConv
  4. class GCN(torch.nn.Module):
  5.     def __init__(self, hidden_channels):
  6.         super(GCN, self).__init__()
  7.         torch.manual_seed(1234567)
  8.         self.conv1 = GCNConv(dataset.num_features, hidden_channels)
  9.         self.conv2 = GCNConv(hidden_channels, dataset.num_classes)
  11.     def forward(self, x, edge_index):
  12.         x = self.conv1(x, edge_index)
  13.         x = x.relu()
  14.         x = F.dropout(x, p=0.5, training=self.training)
  15.         x = self.conv2(x, edge_index)
  16.         return x
  18. model = GCN(hidden_channels=16)
  19. print(model)
  20. >>>
  21. GCN(
  22.   (conv1): GCNConv(1433, 16)
  23.   (conv2): GCNConv(16, 7)
  24. )
  1. model = GCN(hidden_channels=16)
  2. model.eval()
  4. out = model(data.x, data.edge_index)
  5. visualize(out, color=data.y)

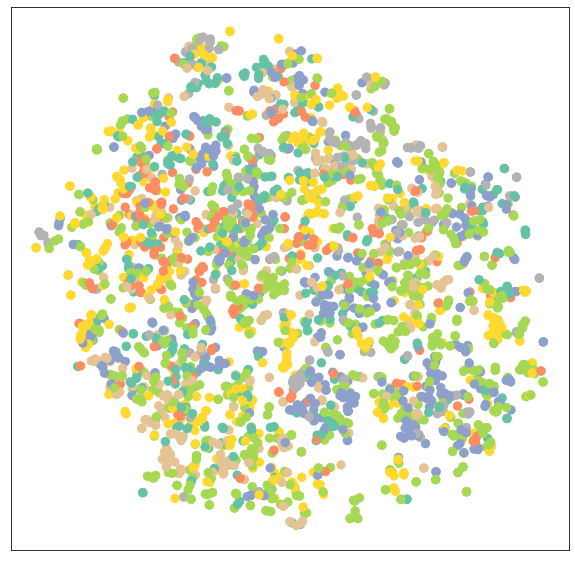
image.png
正如人们所见，至少存在某种聚类（例如，对于“蓝色”节点），但我们当然可以通过训练我们的模型做得更好。 训练和测试过程再次相同，但这次我们使用节点特征 x 和图连通性 edge_index 作为我们 GCN 模型的输入。

  1. from IPython.display import Javascript  # Restrict height of output cell.
  2. display(Javascript('''google.colab.output.setIframeHeight(0, true, {maxHeight: 300})'''))
  4. model = GCN(hidden_channels=16)
  5. optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
  6. criterion = torch.nn.CrossEntropyLoss()
  8. def train():
  9.       model.train()
  10.       optimizer.zero_grad()  # Clear gradients.
  11.       out = model(data.x, data.edge_index)  # Perform a single forward pass.
  12.       loss = criterion(out[data.train_mask], data.y[data.train_mask])  # Compute the loss solely based on the training nodes.
  13.       loss.backward()  # Derive gradients.
  14.       optimizer.step()  # Update parameters based on gradients.
  15.       return loss
  17. def test():
  18.       model.eval()
  19.       out = model(data.x, data.edge_index)
  20.       pred = out.argmax(dim=1)  # Use the class with highest probability.
  21.       test_correct = pred[data.test_mask] == data.y[data.test_mask]  # Check against ground-truth labels.
  22.       test_acc = int(test_correct.sum()) / int(data.test_mask.sum())  # Derive ratio of correct predictions.
  23.       return test_acc
  26. for epoch in range(1, 101):
  27.     loss = train()
  28.     print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
  1. test_acc = test()
  2. print(f'Test Accuracy: {test_acc:.4f}')
  3. >>>
  4. Test Accuracy: 0.8150

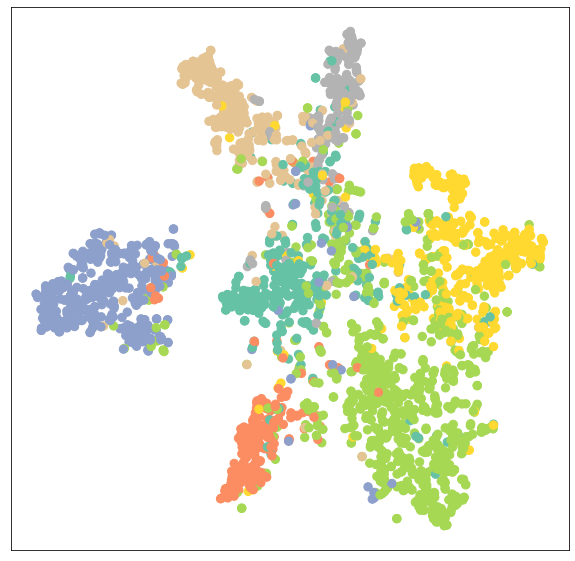
就在那里！ 通过简单地将线性层与 GNN 层交换，我们可以达到 81.5% 的测试准确率！ 这与我们的 MLP 获得的 59% 的测试准确率形成鲜明对比，表明关系信息在获得更好的性能方面起着至关重要的作用。

我们还可以通过查看我们训练模型的输出嵌入再次验证这一点，现在它可以产生更好的同一类别节点聚类。

  1. model.eval()
  3. out = model(data.x, data.edge_index)
  4. visualize(out, color=data.y)

image.png

结论

在本章中，您已经了解了如何将 GNN 应用于现实世界的问题，特别是如何有效地使用它们来提高模型的性能。 在下一节中，我们将研究 GNN 如何用于图分类任务。

练习

为了获得更好的模型性能并避免过度拟合，基于额外的验证集选择最佳模型通常是一个好主意。 Cora 数据集提供了一个验证节点设置为 data.val_mask，但我们还没有使用它。 您能否修改代码以选择和测试验证性能最高的模型？ 这将使测试性能达到 82% 的准确度。

GCN 在增加隐藏特征维数或层数时表现如何？ 增加层数有帮助吗？