问题描述

设计一个满足以下要求的比赛日程表：
(1)每个选手必须与其他n-1个选手各赛一次；
(2)每个选手一天只能赛一次；
(3)循环赛一共进行n-1天。

按分治策略，将所有的选手分为两半，n个选手的比赛日程表就可以通过为n/2个选手设计的比赛日程表来决定。递归地用这种一分为二的策略对选手进行分割，直到只剩下2个选手时，比赛日程表的制定就变得很简单。这时只要让这2个选手进行比赛就可以了。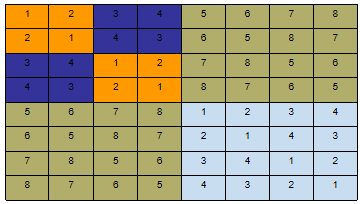
image.png

  1. void gametable(int k)
  2. {       
  3.     int a[100][100];
  4.     int n,temp,i,j,p,t;
  5.     n=2;//k=0两个参赛选手日程可以直接求得
  6.     a[1][1]=1;a[1][2]=2;
  7.     a[2][1]=2;a[2][2]=1;
  8.     for(t=1;t<k;t++)//迭代处理，依次处理^n....2^k个选手的比赛日程
  9.     {
  10.         temp=n;n=n*2;//填左下角元素
  11.         for(i=temp+1;i<=n;i++)
  12.             for(j=1;j<=temp;j++)
  13.                 a[i][j]=a[i-temp][j]+temp;//左下角和左上角元素的对应关系
  14.         for(i=1;i<=temp;i++)//将左下角元素抄到右上角
  15.             for(j=temp+1;j<=n;j++)
  16.                 a[i][j]=a[i+temp][(j+temp)%n];
  17.         for(i=temp+1;i<=n;i++)//将左上角元素抄到右下角
  18.             for(j=temp+1;j<=n;j++)
  19.                 a[i][j]=a[i-temp][j-temp];
  21.     }
  22.     printf("参赛人数为:%d\n(第i行第j列表示和第i个选手在第j天比赛的选手序号)\n",n);
  23.     for(i=1;i<=n;i++)
  24.         for(j=1;j<=n;j++)
  25.         {
  26.             printf("%d ",a[i][j]);
  27.                 if(j==n)
  28.                 printf("\n");
  30.         }
  31. }

考题：
设有n=2k个运动员要进行循环赛,现设计一个满足以下要求的比赛日程表:每个选手必须与其他n-1名选手比赛各一次;每个选手一天至多只能赛一次;循环赛要在最短时间内完成.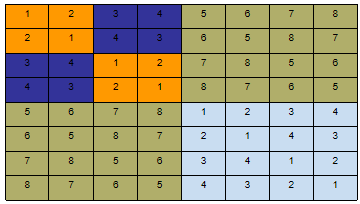
image.png
(1)（4分）循环赛最少需要进行( n-1 )天.
(2)（6分）当n=23=8时,请画出循环赛日程表:1 2 3 4 5 6 7