1、对下图所示的连通网络G，用克鲁斯卡尔(Kruskal)算法求G的最小生成树T,请写出在算法执行过程中，依次加入T的边集TE中的边。说明该算法的贪心策略和算法的基本思想，并简要分析算法的时间复杂度。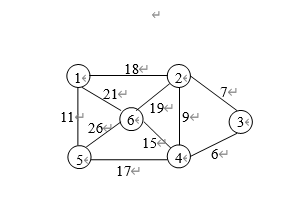
    image.png
    答：
    解集：TE={(3,4), (2,3),(1,5),（4,6）（4,5）}
    贪心策略：每次都在连接两个不同连通分量的边中选权值最小的边。
    基本思想：首先将图中所有顶点都放到生成树中，然后每次都在连接两个不同连通分量的边中选权值最小的边，将其放入生成树中，直到生成树中有n-1条边。
    时间复杂度为：O(eloge)

    2、一个旅行者要驾车从 A 地到 B 地，A、B 两地间距离为 s。A、B 两地之间有n 个 加 油 站 ， 已 知 第 i 个 加 油 站 离 起 点 A 的 距 离 为 di 公 里 ， 0= d1< d2 < ….< dn < s，车加满油后可行驶 m 公里，出发之前汽车油箱为空。 应如何加油使得从 A 地到 B 地沿途加油次数最少？给出用贪心法求解该最优 化问题的贪心选择策略，写出求该最优化问题的最优值和最优解的贪心算法， 并分析算法的时间复杂性。

    1. 贪心选择策略：起点的加油站起每次加满油后不加油行驶尽可能远，油箱中的油耗尽前所能到达的最远的油站为止，在该油站再加满油。 
    3. 算法 MINSTOPS 
    5. 输入：
    6. A、B 两地间的距离 s，A、B 两地间的加油站数 n，车加满油后可行驶的公里数 m，
    7. 存储各加油站离起点 A 的距离的数组 d[1..n]。 
    9. 输出：
    10. 从 A 地到 B 地的最少加油次数 k 以及最优解 x[1..k]（x[i]表示第 i 次加油的加油序号），
    11. 若问题无解，则输出 no solution
    13.     d[n+1]=s; //设置虚拟加油站第 n+1 站。 
    14.     for i=1 to n 
    15.         if d[i+1]-d[i]>m then 
    16.             output “no solution”; 
    17.             return //无解，返回 
    18.         end if 
    19.     end for 
    21.     k=1; x[k]=1 //在第 1 站加满油。 
    22.     s1=m //s1 为用汽车的当前油量可行驶至的地点与 A 点的距离 
    23.     i=2 
    24.     while s1<s 
    25.         if d[i+1]>s1 then //以汽车的当前油量无法到达第 i+1 站。 
    26.             k=k+1; 
    27.             x[k]=i         //在第 i 站加满油。 
    28.             s1=d[i]+m     //刷新 s1 的值
    29.         end if 
    30.         i=i+1 
    31.     end while 
    32.     output k, x[1..k] 
    33. MINSTOPS 
    35. 最坏情况下的时间复杂性：Θ(n)

    3、写出用背包问题贪心算法解决下列实例的过程。
    P=(18,12,4,1)
    W=(12,10,8,3)
    M=25 

    1. 实例符合 P(i)/W(i)≥P(i+1)/W(i+1)的顺序。 
    2.     CU←25,X←0 
    3.     W[1]< CU:    x[1]←1; CU←CU-W[1]=13; 
    4.     W[2]< CU:    x[2]←1; CU←CU-W[2]=3; 
    5.     W[3]>CU:    x[3]←CU/ W[3]=3/8; 
    6.     实例的解为：（1，1，3/8，0）

    4、设有 n 种面值为:
    d1≥d2≥……≥dn的钱币，需要找零钱 M，如何选择钱币 dk，的数目 Xk，满足 d1×Xi＋……dn×Xn=M ，使得 Xi＋……Xn 最小
    请选择贪心策略，并设计贪心算法。

    1. 贪心原则：每次选择最大面值硬币。 
    2.     CU←M;
    3.     i←1;
    4.     X←0;        // X 为解向量 
    6.     While CU≠0 do 
    7.         X[i]←CU div d[i]         // X[i]为第 i 中硬币数 
    8.         CU←CU-d[i]*X[i] 
    9.         i←i+1; 
    10.     repeat

    5、有 n 个物品，已知 n=7, 利润为 P=(10,5,15,7,6,18,3)，重量 W=(2,3,5,7,1,4,1)， 背包容积 M=15,物品只能选择全部装入背包或不装入背包，设计贪心算法，并讨论是否可获 最优解。

    1. 1、定义结构体数组 G，将物品编号、利润、重量作为一个结构体：
    2.     例如 G[k]={1,10,2} 求最优解，按利润/重量的递减序，有
    3.     {5,6,1,6} {1,10,2,5}{6,18,4,9/2} {3,15,5,3} {7,3,1,3}{2,5,3,5/3} {4,7,7,1} 
    5. 算法
    6.     procedure KNAPSACK(P，W，M，X，n) 
    7.         //P(1：n)和 W(1；n)分别含有按P(i)/W(i)≥P(i+1)/W(i+1)排序的 n 件物品的效益值和重量。
    8.         //M 是背包的容量大小，而 x(1：n)是解向量// 
    9.     real P(1：n)，W(1：n)，X(1：n)，M，cu； 
    10.     integer i，n； 
    11.     X←0     //将解向量初始化为零// 
    12.     cu←M     //cu 是背包剩余容量// 
    14.     for i←1 to n do 
    15.         if W(i)>cu then 
    16.             exit 
    17.         endif 
    18.         X(i) ←1 
    19.         cu←cu-W(i) 
    20.     repeat 
    21.     end GREEDY-KNAPSACK 
    24. 根据算法得出的解： 
    25. X=    （1,1,1,1,1,0,0）获利润 52， 而解 
    26.     （1,1,1,1, 0, 1,0）可获利润 54因此贪心法不一定获得最优解。

    6、试用贪心算法求解下列问题：将正整数 n 分解为若干个互不相同的自然数之和，使这些自然数的乘积最大。（15 分） 

    1. #include<iostream>
    2. #include<cstdio>
    3. using namespace std;
    4. //把自然数N分解成若干个互不相同的正整数，使乘积最大；
    5. /**
    6. 题意挺晦涩的，就是说要维持这个会议召开需要满足几个条件，而要会议召开最久需要这个条件尽可能久的维持
    7. 接着就需要了将整数N分解任意个不同的整数，使这些整数的乘积最大
    8. 将N分解为N=a1+a2+a3+..+ak
    9. 可以归纳出这么一些规律
    10. 1.a1>1  如果a1=1，那么将a1加到ak上，必然使得到的这个乘积大于原来的乘积
    11. 2.2>=a[i+1]-a[i]>=1,因为如果出现>2,可以将a[i+1],a[i]改为a[i+1]-1,a[i]+1，使得到的乘积更大
    12. 3.最多只有一个i,使得a[i+1]-a[i]=2
    13.   反证法，假设i<j,并且a[i+1]-a[i]=2,a[j+1]-a[j]=2,那么将a[i],a[j+1]替换成a[i]+1,a[j+1]-1
    14.   将使得乘积更大
    15. 4.a1<=3 如果a1>=4,那么将a1,a2替换成2,a1-1,a2-1将使得乘积更大
    16. 5.如果a1=3,并且存在一个i使得a[i+1]-a[i]=2，那么i一定为t-1
    17. 做法就是求出以2起始的最大连续自然数序列之和sum，使得sum的值不超过输入数n，
    18. 然后分情况讨论：
    19. 设此最大序列为2、3、……、w，则：
    20. 1。若剩余值（n-sum）等于w，则最后输出序列为：3、4、……、w、w+2，即将原最大序列每项加1，再将最后剩余的一个1加到最后一项上。
    21. 2。若剩余值（n-sum）小于w，则从序列的最大项i开始，从大到小依次将每项加1，直到剩余值用完。
    22. */
    23. void dicomp(int n,int a[]) 
    24. { 
    25.     k=1; 
    26.     if(n<3)
    27.     { 
    28.         a[1]=0;
    29.         return;
    30.     }; 
    31.     if(n<5)
    32.     { 
    33.         a[k]=1;
    34.         a[++k]=n-1;
    35.         return;
    36.     }; …………………………（5 分） 
    37.     a[1]=2;
    38.     n-=2; 
    39.     while(n>a[k])
    40.     { 
    41.         k++; 
    42.         a[k]=a[k-1]+1; 
    43.         n-=a[k]; 
    44.     };……………………………（10 分） 
    45.     if(n= =a[k])
    46.     { 
    47.         a[k]++;
    48.         n--;
    49.     }; 
    50.     for(int i=0;i<n;i++) 
    51.         a[k-i]++; 
    52. }……………………………（15 分）

    7、分别用贪心算法、动态规划法、回溯法设计 0-1 背包问题。要求：说明所使用的算法策略；写出算法实现的主要步骤；分析算法的时间。
    答：

    时间复杂度：O(nlogn) 

分析：
    首先计算每种物品单位重量的价值 Vi/Wi，然后，依贪心选择策略，将尽可能多的单位重量价值最高的物品装入背包。
    若将这种物品全部装入背包后，背包内的物品总重量未超过 C，则选择单位重量价值次高的物品并尽可能多地装入背包。
    依此策 略一直地进行下去，直到背包装满为止。 

算法：
void Knapsack(int n,float M,float v[],float w[],float x[]) 
{
    Sort(n,v,w); //按单价降序排列
    int i; 
    for (i=1;i<=n;i++) 
        x[i]=0; 
    float c=M; 
    for (i=1;i<=n;i++) 
    {
        if (w[i]>c) break; 
        x[i]=1; 
        c-=w[i]; 
    }
    if (i<=n) 
        x[i]=c/w[i]; 
}

    （2）动态规划法 O(nc)
    m(i，j)是背包容量为 j，可选择物品为 i，i+1，…，n 时 0-1 背包问题的最优值。由 0-1背包问题的最优子结构性质，可以建立计算 m(i，j)的递归式如下。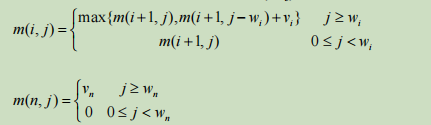
    image.png

    void KnapSack(int v[],int w[],int c,int n,int m[][11]) 
{
    int jMax=min(w[n]-1,c); 

    for (j=0;j<=jMax;j++) 
        /*m(n,j)=0 
        0=<j<w[n]*/ 
        m[n][j]=0; 

    for (j=w[n];j<=c;j++) 
        /*m(n,j)=v[n] 
        j>=w[n]*/ 

        m[n][j]=v[n]; 

    for (i=n-1;i>1;i--) 
    { 
        int jMax=min(w[i]-1,c); 
        for (j=0;j<=jMax;j++) 
            /*m(i,j)=m(i+1,j) 
            0=<j<w[i]*/ 
            m[i][j]=m[i+1][j]; 
        for (j=w[i];j<=c;j++)/*m(n,j)=v[n] 
            j>=w[n]*/ 
            m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]); 
    }

    m[1][c]=m[2][c]; 
    if(c>=w[1]) 
        m[1][c]=max(m[1][c],m[2][c-w[1]]+v[1]);
}

    时间复杂度： O(2n) 
cw:当前重量 
cp:当前价值 
bestp：当前最优值 

void backtrack(int i) 
//回溯法 i 初值 1 
{ 
    if(i > n) //到达叶结点 
    { 
        bestp = cp; 
        return; 
    } 

    if(cw + w[i] <= c)     //搜索左子树 
    { 
        cw += w[i]; 
        cp += p[i]; 
        backtrack(i+1); 
        cw -= w[i]; 
        cp -= p[i]; 
    }
    if(Bound(i+1)>bestp) //搜索右子树
        backtrack(i+1); 
}

    8、通过键盘输入一个高精度的正整数 n(n 的有效位数≤240)，去掉其中任意 s 个数字后，
    剩下的数字按原左右次序将组成一个新的正整数。编程对给定的 n 和 s，寻找一种方案，使
    得剩下的数字组成的新数最小。
    【样例输入】
    178543
    S=4
    【样例输出】
    13 

    为了尽可能地逼近目标，我们选取的贪心策略为：
    每一步总是选择一个使剩下的数最小的数字删去，即按高位到低位的顺序搜索，
    若各位数字递增，则删除最后一个数字，否则删除第一个递减区间的首字符。
    然后回到串首，按上述规则再删除下一个数字。重复以上过程 s 次，剩下的数字串便是问题的解了。 

算法： 
    输入s, n; 
    while（s > 0 ） 
    { 
        i=1; //从串首开始找 
        while (i < length(n)) && (n[i]<n[i+1]) 
        {
            i++;
        } 
        delete(n,i,1); //删除字符串n的第i个字符 
        s--; 
    } 
    while (length(n)>1)&& (n[1]='0') 
        delete(n,1,1); //删去串首可能产生的无用零 
    输出n;

    9、 机器调度问题。
    问题描述：现在有 n 件任务和无限多台的机器，任务可以在机器上得到 处理。每件任务的开始时间为 si，完成时间为 fi，si问题实例：若任务占用的时间范围是{[1，4]，[2，5]，[4，5]，[2，6]，[4，7]}，则按时完成所有任务最少需要几台机器？（提示：使用贪心算法） 画出工作在对应的机器上的分配情况。
    解：