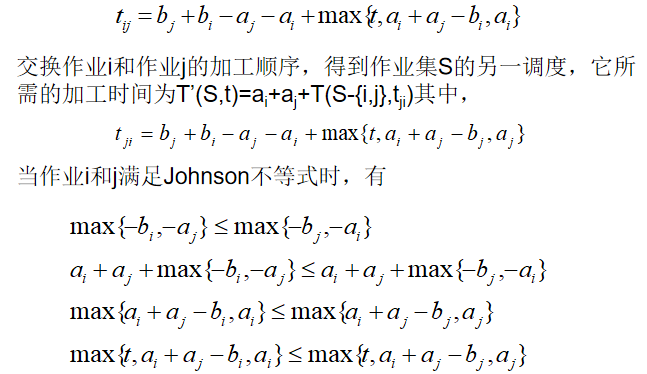问题描述：

n个作业{1，2，…，n}要在由2台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工，然后在M2上加工。M1和M2加工作业i所需的时间分别为a**i和b**i。
流水作业调度问题:要求确定这n个作业的最优加工顺序，使得从第一个作业在机器M1上开始加工，到最后一个作业在机器M2上加工完成所需的时间最少。

分析：

直观上，一个最优调度应使机器M1没有空闲时间，且机器M2的空闲时间最少。在一般情况下，机器M2上会有机器空闲和作业积压2种情况。
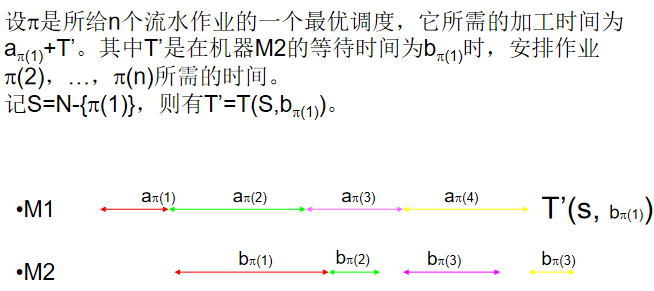
设全部作业的集合为N={1，2，…，n}。SN是N的作业子集。在一般情况下，机器M1开始加工S中作业时，机器M2还在加工其他作业，要等时间t后才可利用。将这种情况下完成S中作业所需的最短时间记为T(S,t)。流水作业调度问题的最优值为T(N,0)。

Johnson不等式

如果作业i和j满足min{bi,aj}≥min{bj,ai}，则称作业i和j满足Johnson不等式。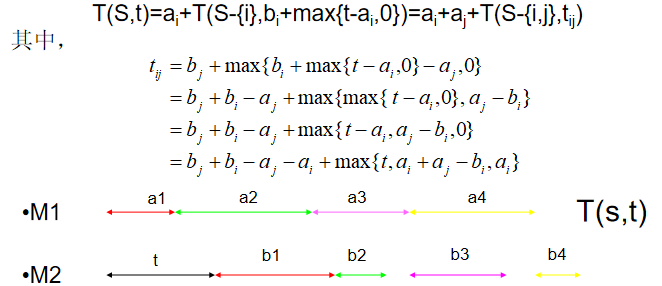

流水作业调度的Johnson法则

算法描述

算法复杂度分析

算法的主要计算时间花在对作业集的排序。因此，在最坏情况下算法所需的计算时间为O(nlogn)。所需的空间为O(n)。

int flowshop(int n,int a[],int b[],int c[]) 
{    //分成两组
    for(int i=0;i<n;i++)
    {    
        d[i].key =a[i]>b[i]?b[i]:a[i];
         d[i].job=a[i]<=b[i];
         d[i].index=i;
    }
    sort(d,n);//从小到大排序
    j=0;  
    k=n-1; 
    for(i=0;i<n;i++)
    {    
        if(d[i].job)    
            c[j++]=d[i].index;
        else                 
            c[k--]=d[i].index;
    }//a组升序，b组降序
    j=a[c[0]];  
    k=j+b[c[0]];
    for(i=1;i<n;i++)
    {     
        j+=a[c[i]];
        k=j<k?k+b[c[i]]:j+b[c[i]];
    }
    return k;
}