问题描述：

在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在n×n格的棋盘上放置n个皇后，任何2个皇后不放在同一行或同一列或同一斜线上。求出共有多少种？
n==4时，2种。n==8,92种。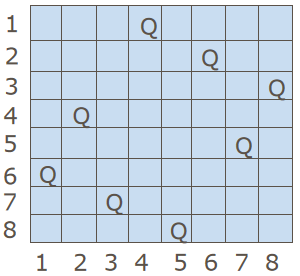
image.png
解向量：(x1, x2, … , xn)
显约束：xi=1,2, … ,n——>一行一个
隐约束:
1)不同列：xi!=xj——->x[j] == x[k]
2)不处于同一正反对角线：|i-j|!=|xi-xj|————>abs(x[j] - x[k]) == abs(k - j)
核心代码中时间复杂度为：O(nn),其中n表示问题的规模

  1. #include <iostream>
  2. using namespace std;
  4. #define Max 20      //定义棋盘的最大值
  5. int x[Max];            //解向量a[i]表示第i行的第a[i]个位置
  6. int sum = 0;        //表示所有情况的个数
  7. int n=0;
  9. bool place(int k)    //定义check函数
  10. {
  11.     for (int j = 1; j < k; j++)    //将第k行与前面的第1~~k-1行进行判断
  12.         if ((abs(x[j] - x[k]) == abs(k - j)) || (x[j] == x[k]))
  13.             //(abs(x[j] - x[k]) == abs(k - j))是否在对角线上
  14.             //(x[j] == x[k])是否在同一列上
  15.             return false;
  16.     return true;
  17. }
  19. void backtrack(int t)    //定义函数,t表示行数
  20. {
  21.     if (t > n)
  22.         sum++;
  23.     else
  24.         for (int i = 1; i <= n; i++)//枚举
  25.         {
  26.             x[t] = i;//解向量数组
  27.             if (place(t))
  28.                 backtrack(t + 1);
  29.         }
  30. }
  32. int main(void)
  33. {
  34.     cout << "请输入n:";
  35.     cin >> n;
  36.     backtrack(1);
  37.     cout << sum;
  38. }

n 皇后问题回溯算法的判别函数 place 的基本流程是什么？
答：将第 K 行的皇后分别与前 k-1 行的皇后比较，看是否与它们相容（不能同一列和同一斜线），如果不相容就返 回 false，测试完毕则返回 true。

请画出用回溯法解4皇后问题的解空间树和搜索空间树：
解空间树：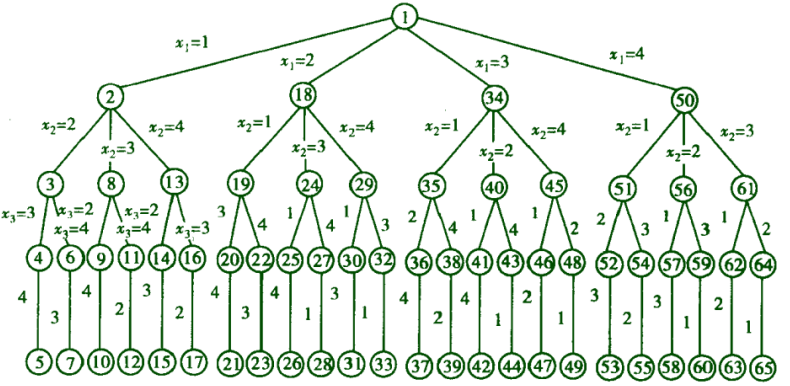
image.png
搜索空间树：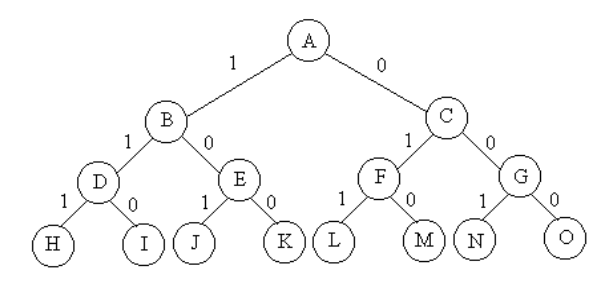
image.png

  1. #include <iostream>
  2. using namespace std;
  4. #define Max 20      //定义棋盘的最大值
  5. int x[Max];            //解向量x[i]表示第i行的第x[i]个位置
  6. int sum = 0;        //表示所有情况的个数
  7. int n=0;
  9. int show(int n)    //定义输出函数
  10. {
  11.     int b[Max][Max] = { 0 };    //定义并初始化b[][]输出数组
  13.     for (int i = 1; i <= n; i++)    //按横列i顺序输出a[i]数组坐标
  14.     {
  15.         b[i][x[i]] = 1;
  16.         printf("(%d,%d)\t", i, x[i]);
  17.     }
  18.     printf("\n");
  19.     for (int p = 1; p <= n; p++)     //按棋盘的横列p顺序标明皇后的位置
  20.     {
  21.         for (int q = 1; q <= n; q++)
  22.         {
  23.             if (b[p][q] == 1)    //在第p行第q列放置一个皇后棋子
  24.                 printf("●");
  25.             else
  26.                 printf("○");
  27.         }
  28.         printf("\n");
  29.     }
  30.     return 0;
  31. }
  33. bool place(int k)    //定义check函数
  34. {
  35.     for (int j = 1; j < k; j++)    //将第k行与前面的第1~~k-1行进行判断
  36.         if ((abs(x[j] - x[k]) == abs(k - j)) || (x[j] == x[k]))
  37.             //(abs(x[j] - x[k]) == abs(k - j))是否在对角线上
  38.             //(x[j] == x[k])是否在一列上
  39.             return false;
  40.     return true;
  41. }
  43. void backtrack(int t)    //定义函数,t表示层数
  44. {
  45.     if (t > n) {
  46.         sum++;
  47.         show(n);
  48.     }
  50.     else
  51.         for (int i = 1; i <= n; i++)//枚举
  52.         {
  53.             x[t] = i;
  54.             if (place(t))
  55.                 backtrack(t + 1);
  56.         }
  57. }
  59. int main(void)
  60. {
  61.     cout << "请输入n:";
  62.     cin >> n;
  63.     backtrack(1);
  64.     cout << sum;
  65. }

image.png

#include "iostream"
#include "cmath"
using namespace std;

#define Max 20      //定义棋盘的最大值
int a[Max];
int show(int S)    //定义输出函数
{
    int i,p,q;
    int b[Max][Max]={0};     //定义并初始化b[][]输出数组

    for(i=1;i<=S;i++)    //按横列i顺序输出a[i]数组坐标
    {
        b[i][a[i]]=1;
        printf("(%d,%d)\t",i,a[i]);
    }
    printf("\n");
    for(p=1;p<=S;p++)     //按棋盘的横列p顺序标明皇后的位置
    {
        for(q=1;q<=S;q++)
        {
            if(b[p][q]==1)     //在第p行第q列放置一个皇后棋子
                printf("●");
            else
                printf("○");
        }
        printf("\n");
    }
    return 0;
}

int check(int k)    //定义check函数
{
    int i;
    for(i=1;i<k;i++)    //将第k行与前面的第1~~k-1行进行判断
    {
        if((a[i]==a[k]) || (a[i]-a[k]==k-i) || (a[i]-a[k]==i-k))    //检查是否有多个皇后在同一条直线上
        {
            return 0;
        }
    }
    return 1;
}

void check_m(int num)    //定义函数
{
    int k=1,count=0;
    printf("The possible configuration of N queens are:\n");
    a[k]=1;
    while(k>0)
    {
        if(k<=num && a[k]<=num)    //从第k行第一列的位置开始，为后续棋子选择合适位子
        {
            if(check(k)==0)    //第k行的a[k]列不能放置皇后
            {
                a[k]++;        //继续探测当前行的下一列：a[k]+1
            }
            else
            {
                k++;         //第K行的位置已经确定了，继续寻找第k+1行皇后的位置
                a[k]=1;      //从第一列开始查找
            }
        }
        else
        {
            if(k>num)     //若满足输出数组的要求则输出该数组
            {
                count++;
                printf("[%d]:  ",count);
                show(num);    //调用输出函数show()
            }
            //如果k>num会执行下面两行代码，因为虽然找到了N皇后问题的一个解，但是要找的是所有解，需要回溯，从当前放置皇后的下一列继续探测
            //如果a[k]>num也会执行下面两行代码，就是说在当前行没有找到可以放置皇后的位置，于是回溯，从上一行皇后位置的下一列继续探测
            k--;      //棋子位置不符合要求，则退回前一步
            a[k]++;   //继续试探下一列位置
        }
    }
    printf("The count is: %d \n",count);
}

int main(void)
{
    int N,d;
    //system("color 2a");
    do
    {
        printf("********************N皇后问题系统*********************\n\n");
        printf("                  1. 四皇后问题                        \n");
        printf("                  2. 八皇后问题                        \n");
        printf("                  3. N 皇后问题(N<20)                  \n");
        printf("                  4. 退出                              \n");
        printf("******************************************************\n");
        printf("\n    从数字1-4之间的数选择需要的操作\n\n"); /*提示输入选项*/
        printf("      请输入你要选择的功能选项:__\n");
        scanf("%d",&d); 
        switch(d)
        {
        case 1:
            check_m(4);      //4皇后问题
            break; 
        case 2:
            check_m(8);     //8皇后问题
            break; 
        case 3:
            printf("请输入N的值：_");
            fflush(stdin);      //清除缓冲
            scanf("%d",&N);
            printf("\n");
            if(N>0&&N<20)
            {
                check_m(N);    //N皇后问题
                break;
            }
            else
            {
                printf("输入错误，请从新输入：");
                printf("\n\n");
                break; 
            }
        case 4:
            exit(0);     //程序结束
        }
    }while(1);
    system("pause");
    return 0;
}