单源最短路径

给定带权有向图G =(V,E)，其中每条边的权是非负实数。另外，还给定V中的一个顶点，称为源。现在要计算从源到所有其他各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。

Dijkstra基本思想

设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时，S中仅含有源。设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其他顶点之间的最短路径长度。
例如，对图中的有向图，应用Dijkstra算法计算从源顶点1到其他顶点间最短路径的过程列在下页的表中。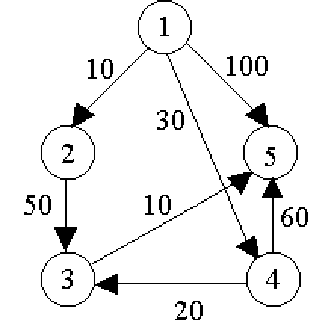
image.png
Dijkstra算法的迭代过程：

迭代 S u dist[2] dist[3] dist[4] dist[5]
初始 {1} - 10 maxint 30 100
1 {1,2} 2 10 60 30 100
2 {1,2,4} 4 10 50 30 90
3 {1,2,4,3} 3 10 50 30 60
4 {1,2,4,3,5} 5 10 50 30 60

算法的正确性和计算复杂性

(1)贪心选择性质
(2)最优子结构性质
(3)计算复杂性
对于具有n个顶点和e条边的带权有向图，如果用带权邻接矩阵表示这个图，那么Dijkstra算法的主循环体需要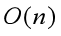image.png时间。这个循环需要执行n-1次，所以完成循环需要 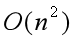image.png时间。算法的其余部分所需要时间不超过image.png。

  1. void Dijkstra(int n, int v, int dist[], int prev[], int c[][6])
  2. {
  3.     //n：共有n个节点      v:从v点开始
  4.     bool s[20] = {};
  5.     for (int i = 1; i <= n; i++)
  6.     {
  7.         dist[i] = c[v][i]; 
  8.         s[i] = false;       //初始化
  9.         if(dist[i] == MAX)
  10.             prev[i] = 0;
  11.         else 
  12.             prev[i] = v;//表示v点可以到达i点
  13.     }
  15.     dist[v] = 0;
  16.     s[v] = true;//起点可以到达起点，并且权值为0
  18.     for (int i = 1; i < n; i++)
  19.     {
  20.         int temp = MAX;
  21.         int u = v;
  22.         for (int j = 1; j <= n; j++)
  23.         {
  24.             if ((!s[j]) && (dist[j] < temp))
  25.             { 
  26.                  u = j; 
  27.                  temp = dist[j]; 
  28.             }
  29.         }
  30.         s[u] = true;
  33.         for (int j = 1; j <= n; j++)
  34.             if ((!s[j]) && (c[u][j] < MAX)) {
  35.                 int newdist = dist[u] + c[u][j];
  36.                 if (newdist < dist[j])//权值变小则更新
  37.                     dist[j] = newdist;
  38.                 prev[j] = u;
  39.             }
  40.     }
  41. }
#include<iostream>
using namespace std;
#define MAX 100000000

/*
1）dist[]存储第i个节点到起始点的距离，s[i]=true 代表第i个点是否已经遍历过。
2）遍历所有s[i] == false的点，找出dist[i]最小的点 u。
3）遍历与u相连的点j，用 min(dist[j], dist[u] + c[u][j])来更新 dist[j]。
4）将s[u] = true;
5) 如果还存在未遍历的点，返回2）
*/
void Dijkstra(int n, int v, int dist[], int prev[], int c[][6])
{
    //n：共有n个节点      v:从v点开始
    bool s[20] = {};
    for (int i = 1; i <= n; i++)
    {
        dist[i] = c[v][i];
        s[i] = false;       //初始化
        if(dist[i] == MAX)
            prev[i] = 0;
        else
            prev[i] = v;//表示v点可以到达i点
    }

    dist[v] = 0;
    s[v] = true;//起点可以到达起点，并且权值为0

    for (int i = 1; i < n; i++)
    {
        int temp = MAX;
        int u = v;
        for (int j = 1; j <= n; j++)
        {
            if ((!s[j]) && (dist[j] < temp))
            {
                u = j;
                temp = dist[j];
            }
        }
        s[u] = true;

        for (int j = 1; j <= n; j++)
            if ((!s[j]) && (c[u][j] < MAX)) {
                int newdist = dist[u] + c[u][j];
                if (newdist < dist[j]){//权值变小则更新
                    dist[j] = newdist;
                    prev[j] = u;
                }
            }
    }
}

void trushback(int n, int prev[]) {
    if (n == 1)
        return;
    trushback(prev[n], prev);
    cout << prev[n] << "---->";

    if (n == 5)         //输出最后一次
        cout << n<<endl;
}

int main(){
    int dist[6];//存储起点到个点的最短路径
    int prev[6];//prev[i] = v;表示v点可以到达i点
    int c[6][6]={};
    for (int i = 0; i < 6; i++)
        for (int j = 0; j < 6; j++)
            c[i][j] = MAX;
    c[1][2] = 10;c[3][5] = 10;c[4][3] = 20;
    c[1][4] = 30;c[2][3] = 50;c[4][5] = 60;c[1][5] = 100;

    Dijkstra(5, 1,dist, prev, c);

    for (int i = 2; i < 6; i++)
        cout <<"from 1 to "<<i<< " ： dist[" << i << "]= " << dist[i] << "  "<< endl;

    cout<<endl;
    for (int i = 1; i < 6; i++)
        cout<<"prev[" << i << "]= " << prev[i] << "  ";
    cout << endl;

    for (int i = 1; i < 6; i++)
        cout<<i<<" 的上一位："<< prev[i] << endl;
    cout << endl;

    cout<<"the path from 1 to 5 is:"<<endl;
    trushback(5, prev);
    cout<<endl;
    system("pause");
    return 0;
}

运行结果：
from 1 to 2 ： dist[2]= 10
from 1 to 3 ： dist[3]= 50
from 1 to 4 ： dist[4]= 30
from 1 to 5 ： dist[5]= 60

prev[1]= 0  prev[2]= 1  prev[3]= 4  prev[4]= 1  prev[5]= 3
1 的上一位：0
2 的上一位：1
3 的上一位：4
4 的上一位：1
5 的上一位：3

the path from 1 to 5 is:
1---->4---->3---->5