递归算法总体思想：将要求解的较大规模的问题分割成k个更小规模的子问题。
分治法的设计思想是，将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。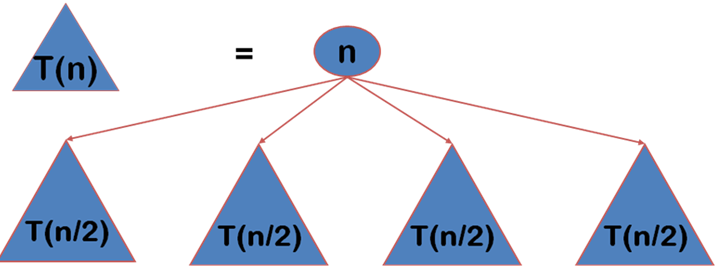

2.1 递归的概念

• 由分治法产生的子问题往往是原问题的较小模式，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，子问题缩小到很容易直接求解——递归过程产生。
• 直接或间接地调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数。
• 分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

递归小结：
优点：结构清晰，可读性强，而且容易用数学归纳法来证明算法的正确性，因此它为设计算法、调试程序带来很大方便。
缺点：递归算法的运行效率较低，无论是耗费的计算时间还是占用的存储空间都比非递归算法要多。

典型问题

全排列
整数划分
汉诺塔问题