找出X={x1,x2,x,3,x4,x5…….} Y={y1,y2,y3,y4……}最长公共子序列

    2个序列的最长公共子序列包含了这2个序列的前缀的最长公共子序列。因此，最长公共子序列问题具有最优子结构性质。
    由最优子结构性质可建立递归关系如下：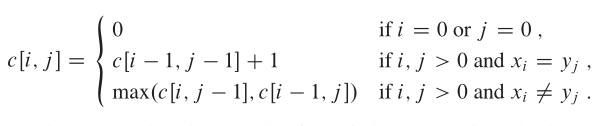
    image.png

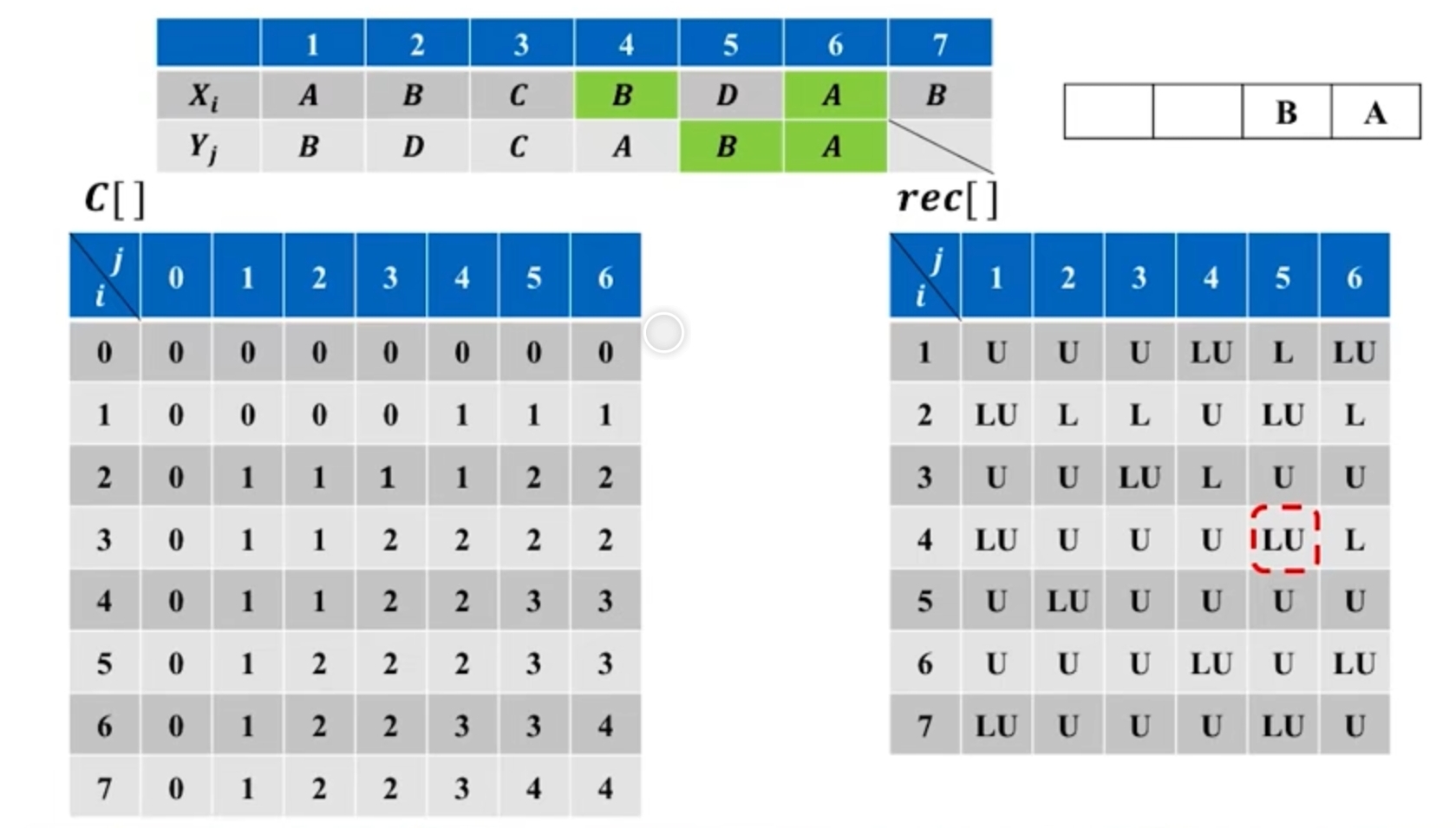
    Screenshot_20220322_234851.jpg
    Screenshot_20220322_200152_tv.danmaku.bili_edit_581003621199813.jpg

    1. void LSCLengh(int m, int n, char x[], char y[]) {
    2.     //m是x数组长度
    3.     //n是y数组长度
    4.     //c[m+1][n+1]数组是辅助空间，记录
    5.     //b[m+1][n+1]数组记录 1-LeftUp、2-UP、3-Left  
    6.     int i, j;
    7.     for (i = 0; i <= m; i++)
    8.         c[i][0] = 0;
    9.     for (i = 1; i <= n; i++)
    10.         c[0][i] = 0;//边缘初始化
    12.     for (i = 1; i <= m; i++) {
    13.         for (j = 1; j <= n; j++)
    14.         {
    15.             if (x[i] == y[j])
    16.             {
    17.                 c[i][j] = c[i - 1][j - 1]+1;
    18.                 b[i][j] = 1;
    19.             }
    20.             else if(c[i-1][j]>=c[i][j-1]) 
    21.             {
    22.                 c[i][j] = c[i - 1][j];
    23.                 b[i][j] = 2;
    24.             }
    25.             else
    26.             {
    27.                 c[i][j] = c[i][j - 1];
    28.                 b[i][j] = 3;
    29.             }
    30.         }
    31.     }
    32. }
    34. //构造最长公共子序列
    35. void  lcs(int i, int j, char x[])
    36. {
    37.     if (i == 0 || j == 0) 
    38.         return;
    39.     if (b[i][j] == 1) 
    40.     {
    41.         lcs(i - 1, j - 1, x);
    42.         cout << x[i];
    43.     }
    44.     else if (b[i][j] == 2) 
    45.         lcs(i - 1, j, x);
    46.     else 
    47.         lcs(i, j - 1, x);
    48. }

    时间复杂度：O(mn)
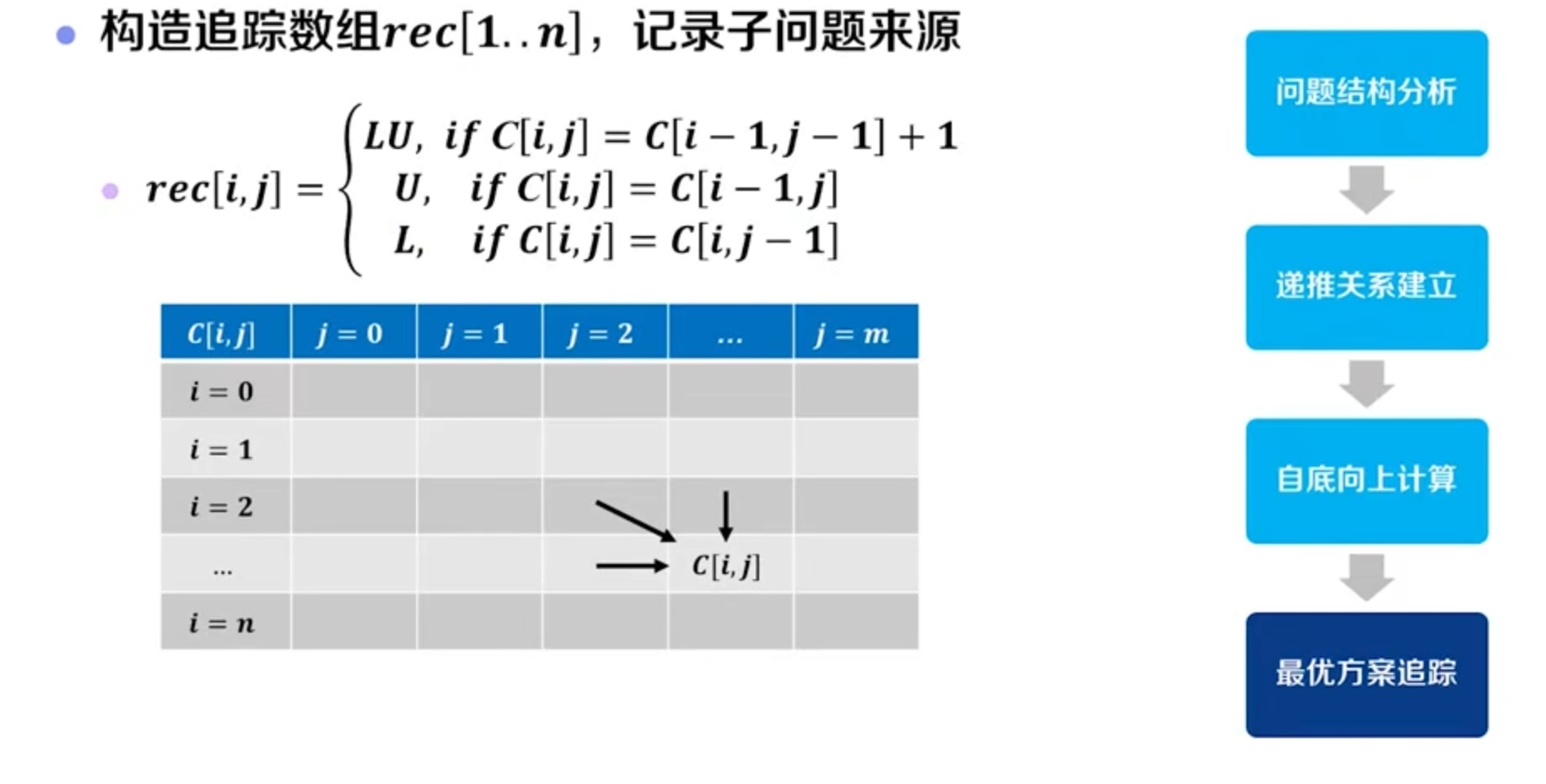
    在算法lcsLength和lcs中，可进一步将数组b省去。事实上，数组元素c[i][j]的值仅由c[i-1][j-1]，c[i-1][j]和c[i][j-1]这3个数组元素的值所确定。对于给定的数组元素c[i][j]，可以不借助于数组b而仅借助于c本身在时间内确定c[i][j]的值是由c[i-1][j-1]，c[i-1][j]和c[i][j-1]中哪一个值所确定的。
    如果只需要计算最长公共子序列的长度，则算法的空间需求可大大减少。事实上，在计算c[i][j]时，只用到数组c的第i行和第i-1行。因此，用2行的数组空间就可以计算出最长公共子序列的长度。进一步的分析还可将空间需求减至O(min(m,n))。

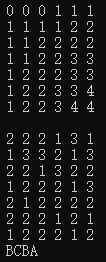
    1. #include<iostream>
    2. using namespace std;
    4. int c[7 + 1][6 + 1];
    5. int b[7 + 1][6 + 1];
    7. void LSCLengh(int m, int n, char x[], char y[]) {
    8.     //m是x数组长度
    9.     //n是y数组长度
    10.     //c[m+1][n+1]数组是辅助空间，记录
    11.     //b[m+1][n+1]数组记录 1-LeftUp、2-UP、3-Left  
    12.     int i, j;
    13.     for (i = 0; i <= m; i++)
    14.         c[i][0] = 0;
    15.     for (i = 1; i <= n; i++)
    16.         c[0][i] = 0;//边缘初始化
    18.     for (i = 1; i <= m; i++) {
    19.         for (j = 1; j <= n; j++)
    20.         {
    21.             if (x[i] == y[j])
    22.             {
    23.                 c[i][j] = c[i - 1][j - 1]+1;
    24.                 b[i][j] = 1;
    25.             }
    26.             else if(c[i-1][j]>=c[i][j-1]) 
    27.             {
    28.                 c[i][j] = c[i - 1][j];
    29.                 b[i][j] = 2;
    30.             }
    31.             else
    32.             {
    33.                 c[i][j] = c[i][j - 1];
    34.                 b[i][j] = 3;
    35.             }
    36.         }
    37.     }
    39.     cout << endl;
    40.     for (i = 1; i <= m; i++) {
    41.         cout << " ";
    42.         for (j = 1; j <= n; j++)
    43.             cout << c[i][j] << " ";
    44.         cout << endl;
    45.     }
    48.     cout << endl;
    49.     for (i = 1; i <= m; i++) {
    50.         cout << " ";
    51.         for (j = 1; j <= n; j++)
    52.             cout << b[i][j] << " ";
    53.         cout << endl;
    54.     }
    55. }
    56. //构造最长公共子序列
    57. void  lcs(int i, int j, char x[])
    58. {
    59.     if (i == 0 || j == 0) 
    60.         return;
    61.     if (b[i][j] == 1) 
    62.     {
    63.         lcs(i - 1, j - 1, x);
    64.         cout << x[i];
    65.     }
    66.     else if (b[i][j] == 2) 
    67.         lcs(i - 1, j, x);
    68.     else 
    69.         lcs(i, j - 1, x);
    70. }
    72. int main() {
    73.     char x[] = {' ', 'A','B','C','B','D','A','B'};
    74.     char y[] = {' ' ,'B','D','C','A','B','A' };
    76.     LSCLengh(7, 6, x, y);
    77.     lcs(7, 6, x);
    78.     return 0;
    79. }

    运行结果：
    image.png