问题描述

设G=( V, E )是一个有向图，图中各边的耗费Cij定义为Cij >0。只要当边( i,j )E时，定义为Cij =0，设‖V‖=n >1，图G中的一条周游路线是包括V中的每个结点在内的一条有向回路。一条周游路线的耗费是这条周游路线上的所有边的耗费之和，所谓旅行商问题就是要在图G中找出一条最小耗费的周游路线。
解空间：排列树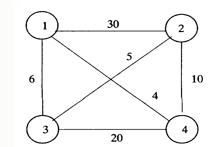
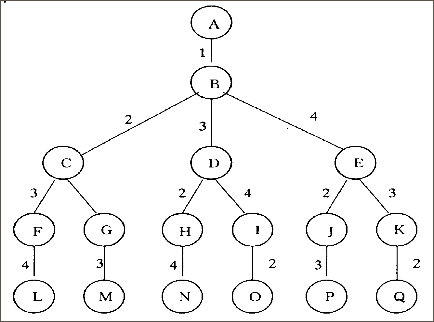
image.png
image.png

  1. void backtrack(int i)
  2. {
  3.     if (i == n)//排列数搜索第n层
  4.     {
  5.         if (a[x[n - 1]][x[n]] < MAX_VALUE && a[x[n]][1] < MAX_VALUE &&(bestc == MAX_VALUE || cc + a[x[n - 1]][x[n]] + a[x[n]][1] < bestc))
  6.             // cc + a[x[n - 1]][x[n]] + a[x[n]][1] < bestc有比当前更优解
  7.             //a[x[n]][1] < MAX_VALUE可以回到起点
  8.             for (int j = 1; j <= n; j++)
  9.                 bestx[j] = x[j];
  10.             bestc = cc + a[x[n - 1]][x[n]] + a[x[n]][1];
  11.     }
  12.     else 
  13.     {
  14.         for (int j = i; j <= n; j++) // 是否可进入x[j]子树?
  15.             if (a[x[i - 1]][x[j]] < MAX_VALUE &&(bestc == MAX_VALUE || cc + a[x[i - 1]][x[j]] < bestc)) 
  16.             {   //a[x[i - 1]][x[j]] < MAX_VALUE表示有边
  17.                 //cc + a[x[i - 1]][x[j]] < bestc有比当前更优解
  18.                 // 搜索子树
  19.                 swap(x, i, j);
  20.                 cc += a[x[i - 1]][x[i]];
  21.                 backtrack(i + 1);
  22.                 cc -= a[x[i - 1]][x[i]];
  23.                 swap(x, i, j);
  24.             }
  25.     }
  26. }

复杂度分析算法backtrack在最坏情况下可能需要更新当前最优解O((n-1)!)次，每次更新bestx需计算时间O(n)，从而整个算法的计算时间复杂性为O(n!)。

#include <iostream>
using namespace std;
const int MAX_VALUE = 0x3f3f3f; //两个点之间没有边,则为无穷大
int n;                      //城市数
int edgenum;                //边数
int currentcost;            //记录当前的路程
int bestcost;               //记录最小的路程(最优)
int Graph[100][100];        //图的边距记录
int x[100];                 //记录行走顺序
int bestx[100];             //记录最优行走顺序

void InPut()
{
    int pos1, pos2, len;     //点1 点2 距离

    cout << "请输入城市数和边数(c e)：";
    cin >> n >> edgenum;

    memset(Graph, MAX_VALUE, sizeof(Graph));

    cout << "请输入两座城市之间的距离(p1 p2 l)：" << endl;
    for (int i = 1; i <= edgenum; ++i)
    {
        cin >> pos1 >> pos2 >> len;
        Graph[pos1][pos2] = Graph[pos2][pos1] = len;
    }
}

//初始化
void Initilize()
{
    currentcost = 0;
    bestcost = MAX_VALUE;
    for (int i = 1; i <= n; ++i)
    {
        x[i] = i;
    }
}

void Swap(int& a, int& b)
{
    int temp;
    temp = a;
    a = b;
    b = temp;
}

void BackTrack(int i) //这里的i代表第i步去的城市而不是代号为i的城市
{
    if (i == n)//i==n时
    {
        //进行一系列判断，注意的是进入此步骤的层数应是叶子节点的父节点，而不是叶子节点
        if (Graph[x[i - 1]][x[i]] < MAX_VALUE && Graph[x[i]][x[1]] < MAX_VALUE && (currentcost + Graph[x[i - 1]][x[i]] + Graph[x[i]][x[1]] < bestcost || bestcost == MAX_VALUE))
        {
            //Graph[x[i - 1]][x[i]] == NoEdge即i-1到i没有边
            //最小(优)距离=当前的距离+当前城市到叶子城市的距离+叶子城市到初始城市的距离
            bestcost = currentcost + Graph[x[i - 1]][x[i]] + Graph[x[i]][x[1]];
            for (int j = 1; j <= n; ++j)
                bestx[j] = x[j];
        }
    }
    else
    {
        for (int j = i; j <= n; ++j)
        {   //是否可进入x[j]子树
            if (Graph[x[i - 1]][x[j]] < MAX_VALUE && (currentcost + Graph[x[i - 1]][x[j]] < bestcost || bestcost == MAX_VALUE))
            {
                Swap(x[i], x[j]);  //这里i 和 j的位置交换了, 所以下面的是currentcost += Graph[x[i - 1]][x[i]];
                currentcost += Graph[x[i - 1]][x[i]];
                BackTrack(i + 1);   //递归进入下一个城市
                currentcost -= Graph[x[i - 1]][x[i]];
                Swap(x[i], x[j]);
            }
        }
    }
}

void OutPut()
{
    cout << "最短路程为：" << bestcost << endl;
    cout << "路线为:" << endl;
    for (int i = 1; i <= n; ++i)
        cout << bestx[i] << " ";
    cout << "1" << endl;//到1结束
}

int main()
{
    InPut();
    Initilize();
    BackTrack(2);
    OutPut();
}

/*
输入
请输入城市数和边数(c e)：4 6
请输入两座城市之间的距离(p1 p2 l)：
1 2 30
1 3 6
1 4 4
2 4 10
2 3 5
3 4 20

输出
最短路程为：25
路线为:
1 3 2 4 1
*/