活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合，是可以用贪心算法有效求解的很好例子。
该问题要求高效地安排一系列争用某一公共资源的活动。贪心算法提供了一个简单、漂亮的方法使得尽可能多的活动能兼容地使用公共资源（使活动数目最多）。

问题描述：

设有n个活动的集合E={1,2,…,n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si j）**，活动i与活动j相容。

s[]起始时间
j[]结束时间
各活动的起始时间和结束时间存储于数组s和f中且按结束时间的非减序排列 
int greedySelector(int s [], int f [], boolean a[],int n)
{
    a[1]=true;
    int j=1;
    int count=1;
    for (int i=2;i<=n;i++) 
    {
        if (s[i]>=f[j]) 
        {
            a[i]=true;
            j=i;
            count++;
        }
        else 
            a[i]=false;
    }
    return count;
}

 由于输入的活动以其完成时间的**非减序**排列，所以算法greedySelector每次总是选择**具有最早完成时间**的相容活动加入集合A中。直观上，按这种方法选择相容活动为未安排活动留下尽可能多的时间。也就是说，该算法的贪心选择的意义是**使剩余的可安排时间段极大化**，以便安排尽可能多的相容活动。<br />**可以用数学归纳法证明**，我们的贪心策略应该是每次选取结束时间最早的活动。直观上也很好理解，按这种方法选择相容活动为未安排活动留下尽可能多的时间。这也是把各项活动按照结束时间单调递增排序的原因。        <br />算法greedySelector的效率极高。当输入的活动已按结束时间的非减序排列，算法只需**O(n**)的时间安排n个活动，使最多的活动能相容地使用公共资源。如果所给出的活动未按非减序排列，可以用**O(nlogn)**的时间重排。 

例：设待安排的11个活动的开始时间和结束时间按结束时间的非减序排列如下：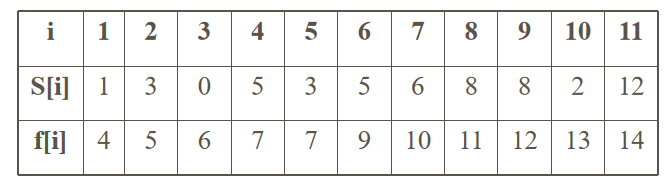


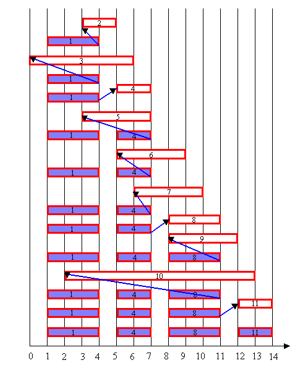
算法greedySelector 的计算过程如图所示。图中每行相应于算法的一次迭代。阴影长条表示的活动是已选入集合A的活动，而空白长条表示的活动是当前正在检查相容性的活动。
若被检查的活动i的开始时间Si小于最近选择的活动j的结束时间fi，则不选择活动i，否则选择活动i加入集合A中。
贪心算法并不总能求得问题的整体最优解。但对于活动安排问题，贪心算法greedySelector却总能求得的整体最优解，即它最终所确定的相容活动集合A的规模最大。这个结论可以用数学归纳法证明。