问题：给定n种物品和一背包。物品i的重量是wi，其价值为pi，背包的容量为c。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?
    分析：问题是n个物品中选择部分物品，可知，问题的解空间是子集树。比如物品数目n=3时，其解空间树如下图，边为1代表选择该物品，边为0代表不选择该物品。使用x[i]表示物品i是否放入背包，x[i]=0表示不放，x[i]=1表示放入。回溯搜索过程，如果来到了叶子节点，表示一条搜索路径结束，如果该路径上存在更优的解，则保存下来。如果不是叶子节点，是中点的节点（如B），就遍历其子节点（D和E），如果子节点满足剪枝条件，就继续回溯搜索子节点。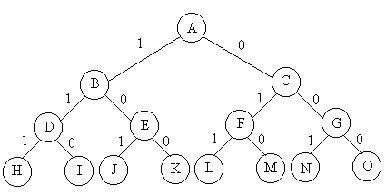
    image.png
    计算上界需要O(n)时间，在最坏情况下有O(2n)个右儿子节点需要计算上界，所以解决01背包问题的回溯法Backtrack所需要的时间复杂度为O(n2**n**)

    1. double Bound(int i)// 计算价值上界
    2. {
    3.     double cleft = c - cw;   //剩余容量
    4.     double bound = cp;
    5.             //以物品单位重量价值递减序装入物品
    6.     while (i <= n && w[i] <= cleft)
    7.     {
    8.         cleft -= w[i];
    9.         bound += p[i];
    10.         i++;
    11.     }
    12.     if (i <= n)// 将物品拆分装满背包，计算最大值
    13.         bound += (float)p[i] / w[i] * cleft;
    14.     return bound;
    15. }
    17. void backtrack(int i)// 搜索第i层结点
    18. {
    19.     if (i > n)  // 到达叶结点
    20.     {
    21.         if (cp > bestp) {      //优于当前值，则更新
    22.             for (int j = 1; j <= n; j++)
    23.                 bestx[j] = x[j];            //将当前最优解保存在bestx数组
    24.             bestp = cp;                     //最优解
    25.         }
    26.         return;
    27.     }
    29.     if (cw + w[i] <= c) // 搜索左子树(限界函数)
    30.     {
    31.         x[i] = 1;
    32.         cw += w[i];//当前放入背包的物品总重量,全局变量
    33.         cp += p[i];
    34.         backtrack(i + 1);
    35.         cw -= w[i];
    36.         cp -= p[i];
    37.     }
    38.     if (Bound(i + 1) > bestp) // 搜索右子树（剪枝函数）
    39.     {
    40.         x[i] = 0;
    41.         backtrack(i + 1);
    42.     }
    43. }
    1. #include<iostream>
    2. using namespace std;
    3. #include<algorithm>
    4. #define n 4         //物品的数量
    5. #define c 7        //背包的容量
    7. int index[n+1]={0,1,2,3,4};//货物序号，排序过程中跟着货物变动
    8. int w[n + 1] = { 0,3,5,2,1 };  //每个物品的重量  第1个商品有效
    9. int p[n + 1] = { 0,9,10,7 ,4};   //每个物品的价值
    11. int x[n + 1] = { };   //x[i]=1代表物品i放入背包，0代表不放入
    13. int cw = 0;  //当前放入背包的物品总重量
    14. int cp = 0;  //当前放入背包的物品总价值
    16. int bestp = 0;      //最优值；当前的最大价值，初始化为0
    17. int bestx[n+1];       //最优解；BestX[i]=1代表物品i放入背包，0代表不放入
    19. double Bound(int i)// 计算价值上界
    20. {
    21.     double cleft = c - cw;   //剩余容量
    22.     double bound = cp;
    23.             //以物品单位重量价值递减序装入物品
    24.     while (i <= n && w[i] <= cleft)
    25.     {
    26.         cleft -= w[i];
    27.         bound += p[i];
    28.         i++;
    29.     }
    30.     if (i <= n)// 将物品拆分装满背包，计算最大值
    31.         bound += (float)p[i] / w[i] * cleft;
    32.     return bound;
    33. }
    35. void backtrack(int i)// 搜索第i层结点
    36. {
    37.     if (i > n)  // 到达叶结点
    38.     {
    39.         if (cp > bestp) {
    40.             for (int j = 1; j <= n; j++)
    41.                 bestx[j] = x[j];            //将当前最优解保存在bestx数组
    42.             bestp = cp;                     //最优解
    43.         }
    44.         return;
    45.     }
    47.     if (cw + w[i] <= c) // 搜索左子树(限界函数)
    48.     {
    49.         x[i] = 1;
    50.         cw += w[i];//当前放入背包的物品总重量,全局变量
    51.         cp += p[i];
    52.         backtrack(i + 1);
    53.         cw -= w[i];
    54.         cp -= p[i];
    55.     }
    56.     if (Bound(i + 1) > bestp) // 搜索右子树（剪枝函数）
    57.     {
    58.         x[i] = 0;
    59.         backtrack(i + 1);
    60.     }
    61. }
    63. void mySort(int w[],int p[]){
    64.     for(int i=1;i<=n;i++)
    65.         for(int j=1;j<n;j++){
    66.             if((p[j]/(double)w[j])<(p[j+1]/(double)w[j+1])){
    67.                     swap(p[j],p[j+1]);
    68.                     swap(w[j],w[j+1]);
    69.                     swap(index[j],index[j+1]);
    70.             }
    71.     }
    72. }
    74. int main()
    75. {
    76.     mySort(w,p);
    77.     /*
    78.         由单价降序排列
    79.         第一个货物对应货物4
    80.         第二个货物对应货物3
    81.         第三个货物对应货物1
    82.         第四个货物对应货物2
    83.     */
    85.     backtrack(1);
    86.     cout << "最大价值：" << bestp << endl;
    87.     for (int i = 1; i <= n; i++)
    88.         cout << "货物" << index[i] << "："<< bestx[i] << endl;
    89.     return 0;
    90. }
    92. 运行结果：
    93. 最大价值：20
    94. 货物4：1
    95. 货物3：1
    96. 货物1：1
    97. 货物2：0
    #include<iostream>
using namespace std;

#define n 3         //物品的数量  
#define c 16        //背包的容量  

int w[n] = {10,8,5 };  //每个物品的重量  
int p[n] = { 5,4,1 };   //每个物品的价值  
int x[n] = { 0,0,0 };   //x[i]=1代表物品i放入背包，0代表不放入  

int cw = 0;  //当前放入背包的物品总重量  
int cp = 0;  //当前放入背包的物品总价值  

int bestp = 0;      //最优值；当前的最大价值，初始化为0  
int bestx[n];       //最优解；BestX[i]=1代表物品i放入背包，0代表不放入  

//t = 0 to N-1  

double Bound(int i)         //计算价值上界
{
    double cleft = c - cw;  // 剩余容量
    double bound = cp;
        // 以物品单位重量价值递减序装入物品
    while (i < n && w[i] <= cleft)
    {
        cleft -= w[i];
        bound += p[i];
        i++;
    }
    if (i < n) // 将物品拆分装满背包，计算最大值
        bound += (float)p[i] / w[i] * cleft;
    return bound;
}

void backtrack(int i)   // 搜索第i层结点
{
    if (i >= n)          // 到达叶结点
    {
        if (cp > bestp)
        { 
            for (int j = 0; j < n; j++)
                bestx[j] = x[j];        //将当前最优解保存在bestx数组
            bestp = cp;                 //最优解
        }
        return;
    }
    if (cw + w[i] <= c) // 搜索左子树
    {
        x[i] = 1;
        cw += w[i];
        cp += p[i];
        backtrack(i + 1);
        cw -= w[i];
        cp -= p[i];
    }
    if (Bound(i + 1) > bestp)   //搜索右子树
    {
        x[i] = 0;
        backtrack(i + 1);
    }
}

int main()
{
    backtrack(0);
    cout << "最大价值：" << bestp << endl;
    for (int i = 0; i < n; i++)
        cout << "货物" << i << "："<< bestx[i] << endl;
    return 0;
}

    运行结果：
    最大价值：6
    货物1：1
    货物2：0
    货物3：1

    #include<iostream>
using namespace std;

#define n 3         //物品的数量  
#define c 16        //背包的容量  

int w[n + 1] = { 0,10,8,5 };  //每个物品的重量  第1个商品有效
int p[n + 1] = { 0,5,4,1 };   //每个物品的价值  
int x[n + 1] = { 0, 0,0,0 };   //x[i]=1代表物品i放入背包，0代表不放入  

int cw = 0;  //当前放入背包的物品总重量  
int cp = 0;  //当前放入背包的物品总价值  

int bestp = 0;      //最优值；当前的最大价值，初始化为0  
int bestx[n+1];       //最优解；BestX[i]=1代表物品i放入背包，0代表不放入  

double Bound(int i)// 计算价值上界
{
    double cleft = c - cw;   //剩余容量
    double bound = cp;
            //以物品单位重量价值递减序装入物品
    while (i <= n && w[i] <= cleft)
    {
        cleft -= w[i];
        bound += p[i];
        i++;
    }

    if (i <= n)// 将物品拆分装满背包，计算最大值
        bound += (float)p[i] / w[i] * cleft;
    return bound;
}

void backtrack(int i)// 搜索第i层结点
{
    if (i > n)  // 到达叶结点
    {
        if (cp > bestp) {
            for (int j = 1; j <= n; j++)
                bestx[j] = x[j];            //将当前最优解保存在bestx数组
            bestp = cp;                     //最优解
        }
        return;
    }
    if (cw + w[i] <= c) // 搜索左子树(限界函数)
    {
        x[i] = 1;
        cw += w[i];
        cp += p[i];
        backtrack(i + 1);
        cw -= w[i];
        cp -= p[i];
    }
    if (Bound(i + 1) > bestp) // 搜索右子树（剪枝函数）
    {
        x[i] = 0;
        backtrack(i + 1);
    }
}

int main()
{
    backtrack(1);
    cout << "最大价值：" << bestp << endl;
    for (int i = 1; i <= n; i++)
        cout << "货物" << i << "："<< bestx[i] << endl;
    return 0;
}

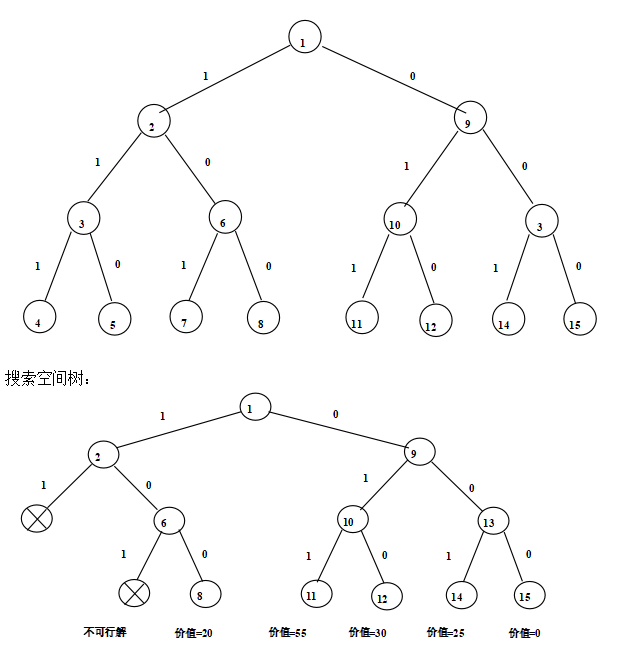
    11，请画出用回溯法解n=3的0-1背包问题的解空间树和当三个物品的
    重量为{20, 15, 10}，价值为{20, 30,25}，背包容量为25时搜索空间树。
    答：解空间树：
    image.png