问题描述：

给定n个矩阵image.png其中 Ai 与Ai +1是可乘的，i=1,2,3……n-1。考察这n个矩阵的连乘积image.png由于矩阵乘法满足结合律，所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。
若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号，则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。
给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。
穷举法：列举出所有可能的计算次序，并计算出每一种计算次序相应需要的数乘次数，从中找出一种数乘次数最少的计算次序
动态规划:将矩阵连乘积 AiAi+1……..Aj 简记为A[i:j] ，这里i≤j ,考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开，i≤k则其相应完全加括号方式为image.png
计算量：A[i:k]的计算量加上A[k+1:j]的计算量，再加上A[i:k]和A[k+1:j]相乘的计算量
特征：计算A[i:j]的最优次序所包含的计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。
矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法求解的显著特征。

建立递归关系：

设计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i][j]，则原问题的最优值为m[1][n]
当i=j时，A[i:j]=Ai，因此，m[i][i]=0，i=1,2,…,n
当i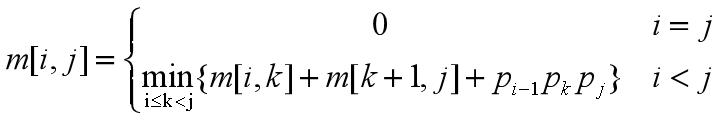image.png
递归地定义m[i][j]为：（i<=k

image.pngimage.png

算法复杂度分析：

算法matrixChain的主要计算量取决于算法中对r，i和k的3重循环。循环体内的计算量为O(1)，而3重循环的总次数为O(n3)。因此算法的计算时间上界为O(n3)。算法所占用的空间显然为O(n2)。
image.png

  1. void MatrixChain(int p[], int n, int m[][N], int s[][N]) {
  2.     for (int i = 1; i <= n; i++)     
  3.                 //矩阵链中只有一个矩阵时，次数为0，注意m[0][X]时未使用的
  4.         m[i][i] = 0;
  6.     for (int r = 2; r <= n; r++) {    
  7.                 //矩阵链长度,从长度为2开始
  8.         for (int i = 1; i <= n - r + 1; i++) {    
  9.                 //根据链长度，控制链最大的可起始点
  10.             int j = i + (r - 1);  
  11.                 //矩阵链的末尾矩阵，注意r-1，因为矩阵链为2时，实际是往右+1
  12.             m[i][j] = m[i][i] + m[i + 1][j] + p[i - 1] * p[i] * p[j];//k=i   
  13.                 //先设置最好的划分方法就是直接右边开刀，后续改正，也可合并到下面的for循环中即让下面的int k=i
  14.             s[i][j] = i;
  15.             for (int k = i + 1; k < j; k++) {   
  16.                 //这里面将断链点从i+1开始，可以断链的点直到j-1为止
  17.                 int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
  18.                 if (t < m[i][j]) {
  19.                     m[i][j] = t;
  20.                     s[i][j] = k;
  21.                 }
  22.             }
  23.         }
  24.     }
  25. }
#include<iostream>
using namespace std;

#define N 7  //N为7，实际表示有6个矩阵
/*
*矩阵链构造函数：构造m[][]和s[][]
*m中存储的值是计算出来的最小乘法次数，比如m[1][5]就是A1A2A3A4A5的最小乘法次数
*s中存储的是获取最小乘法次数时的断链点，s[1][5]对应的就是如何拆分A1A2A3A4A5
*比如S[1][5]=3可表示：(A1A2A3)(A4A5)，当然内部断链还会继续划分A1A2A3
*/
void MatrixChain(int p[], int n, int m[][N], int s[][N]) {
    for (int i = 1; i <= n; i++)     
                //矩阵链中只有一个矩阵时，次数为0，注意m[0][X]时未使用的
        m[i][i] = 0;

    for (int r = 2; r <= n; r++) {    
                //矩阵链长度,从长度为2开始
        for (int i = 1; i <= n - r + 1; i++) {    
                //根据链长度，控制链最大的可起始点
            int j = i + (r - 1);  
                //矩阵链的末尾矩阵，注意r-1，因为矩阵链为2时，实际是往右+1
            m[i][j] = m[i][i] + m[i + 1][j] + p[i - 1] * p[i] * p[j];//k=i   
                //先设置最好的划分方法就是直接右边开刀，后续改正，也可合并到下面的for循环中即让下面的int k=i
            s[i][j] = i;
            for (int k = i + 1; k < j; k++) {   
                //这里面将断链点从i+1开始，可以断链的点直到j-1为止
                int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
                if (t < m[i][j]) {
                    m[i][j] = t;
                    s[i][j] = k;
                }
            }
        }
    }

    for (int i = 1; i <= N - 1; i++) {
        for (int j = 1; j <= N - 1; j++) {
            if (i > j)
                cout << "\t";
            else
                cout << m[i][j] << "\t";
        }
         cout << endl;  
    }
    cout << endl << endl;
    for (int i = 1; i <= N - 1; i++) {
        for (int j = 1; j <= N - 1; j++) {
            if (i >= j)
                cout << "\t";
            else
                cout << s[i][j] << "\t";
        }
        cout << endl;
    }
    cout << endl << endl;

}

//追踪函数：根据输入的i,j限定需要获取的矩阵链的始末位置，s存储断链点

void Traceback(int i, int j, int s[][N]) {
    if (i == j)       //回归条件
    {
        cout << "A" << i;
    }
    else       //按照最佳断点一分为二，接着继续递归
    {
        cout << "(";
        Traceback(i, s[i][j], s);
        Traceback(s[i][j] + 1, j, s);
        cout << ")";
    }
}
int main() {
    int p[N] = { 30,35,15,5,10,20,25 };
    int m[N][N], s[N][N];

    MatrixChain(p, N - 1, m, s);//N-1因为只有六个矩阵
    Traceback(1, 6, s);

    cout << endl << endl;
    system("pause");
    return 0;
}

运行结果：

image.png