问题描述

设计一个递归算法生成n个元素{r1,r2,…,rn}的全排列。
设R={r1,r2,…,rn}是要进行排列的n个元素，Ri=R-{ri}。集合R中元素的全排列记为perm(R)。(ri)perm(Ri)表示在全排列perm(Ri)的每一个排列前加上前缀得到的排列。R的全排列可归纳定义如下：
当n=1时，perm(R)=(r)，其中r是集合R中唯一的元素；
当n>1时，perm(R)由(r1)perm(R1),(r2)perm(R2)，…，(rn)perm(Rn)构成。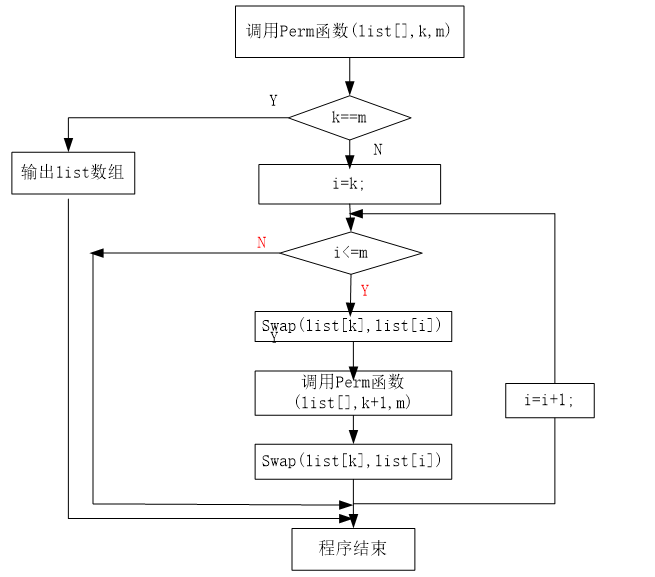
image.png

  1. Template <class Type>
  2. void perm(Type list[],  int k, int m )    //产生[list[k:m]的所有排列
  3. {
  4.     if(k==m)                                空
  5.     {  //只剩下一个元素
  6.         for (int i=0;i<=m;i++)  
  7.             cout<<list[i];
  8.         cout<<endl;
  9.     }
  10.     else  //还有多个元素待排列，递归产生排列
  11.         for (int i=k; i<=m; i++)            空
  12.         {
  13.             swap(list[k]，list[i]);
  14.             perm(list,k+1;m);                空
  15.             swap(list[k],list[i]);         
  16.         }
  17. }
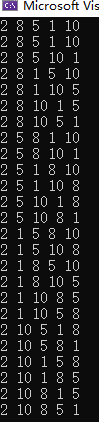
  1. #include<iostream>
  2. using namespace std;
  4. template<class Type>
  5. void Print(Type a[]) {
  6.     for (int i = 0; i < 5; i++)
  7.         cout << a[i] << " ";
  8.     cout << endl;
  9. }
  11. void perim(int a[], int L, int R) {
  12.     if (L == R) {
  13.         Print(a);
  14.         return;
  15.     }
  17.     for (int i = L; i < R; i++) {
  18.         swap(a[i], a[L]);
  19.         cout << a[1] << endl;
  20.         perim(a, L + 1, R);
  21.         swap(a[i],a[L]);
  22.         cout << a[0] << endl;
  23.     }
  25. }
  27. int main()
  28. {
  29.     int a[5]={};
  30.     for (int i = 0; i < 5; i++)
  31.         a[i] = rand() % 10 + 1;
  33.     Print(a);
  34.     perim(a, 2, 5);
  35. }

运行结果
屏幕截图 2022-03-18 225216.png

思考：

对于数组list=(a,b,c,d)
分别写出perm(list,0,3)，perm(list,1,3)，perm(list,2,3)，perm(list,3,3)的结果。
perm(list,0,3) abcd的全排列 24种
perm(list,1,3) 6种
perm(list,2,3) 2种结果
perm(list,3,3) 1种
要了解perm(list,1,3)的过程，有3次调用perm(list,2,3)过程，每次调用perm(list,2,3)有2种结果，所以一共有6种结果。