问题描述

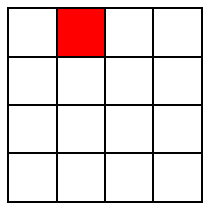
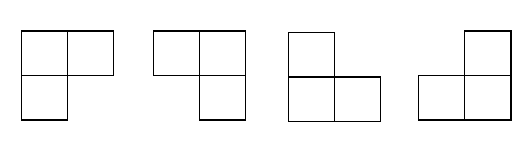
在一个2k×2k 个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。

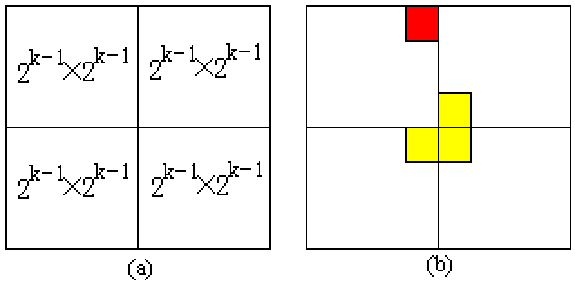
image.png


image.png
  • 当k>0时，将2k×2k棋盘分割为4个2k-1×2k-1 子棋盘(a)所示。
  • 将其3个无特殊方格的子棋盘转化为特殊棋盘，如 (b)所示
  • 将原问题转化为4个较小规模的棋盘覆盖问题。
  • 递归地使用这种分割，直至棋盘简化为棋盘1×1。

image.png

递归方程

设T(k)是算法ChessBoard覆盖一个2kx2k棋盘所需的时间，则从算法的分治策略可知，T(k)满足如下的递归方程：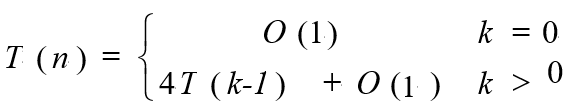
image.png
解此递归方程可解T(k)=O(4k)。由于棋盘覆盖一个棋盘所需的L型骨牌个数为（4k-1）/3，故算法ChessBoard是一个在渐近意义下最优算法。

  1. #include<iostream>  
  2. using namespace std;
  3. int tile = 1;        //L型骨牌的编号(递增)  
  4. int board[100][100];  //棋盘,设计为全局变量  
  5. /* 递归方式实现棋盘覆盖算法
  6. * 输入参数：
  7. * tr--当前棋盘左上角的行号
  8. * tc--当前棋盘左上角的列号
  9. * dr--当前特殊方格所在的行号
  10. * dc--当前特殊方格所在的列号
  11. * size：当前棋盘的:2^k     */
  12. void chessBoard(int tr, int tc, int dr, int dc, int size){
  13.     if (size == 1)    //棋盘方格大小为1,说明递归到最里层  
  14.         return;
  15.     int t = tile++;     //每次递增1  
  16.     int s = size / 2;    //棋盘中间的行、列号(相等的)，用于分割棋盘  
  18.     //检查特殊方块是否在左上角子棋盘中  
  19.     if (dr < tr + s && dc < tc + s)              //在  
  20.         chessBoard(tr, tc, dr, dc, s);
  21.     else{         //不在，将该子棋盘右下角的方块视为特殊方块  
  22.         board[tr + s - 1][tc + s - 1] = t;
  23.         chessBoard(tr, tc, tr + s - 1, tc + s - 1, s);
  24.     }
  26.     //右上角子棋盘中 
  27.     if (dr < tr + s && dc >= tc + s)               //在  
  28.         chessBoard(tr, tc + s, dr, dc, s);
  29.     else{        //不在，将该子棋盘左下角的方块视为特殊方块  
  30.         board[tr + s - 1][tc + s] = t;
  31.         chessBoard(tr, tc + s, tr + s - 1, tc + s, s);
  32.     }
  34.      //左下角子棋盘中 
  35.     if (dr >= tr + s && dc < tc + s)              //在  
  36.         chessBoard(tr + s, tc, dr, dc, s);
  37.     else{            //不在，将右上角视为特殊方块  
  38.         board[tr + s][tc + s - 1] = t;
  39.         chessBoard(tr + s, tc, tr + s, tc + s - 1, s);
  40.     }
  42.     //右下角子棋盘中  
  43.     if (dr >= tr + s && dc >= tc + s)            //在  
  44.         chessBoard(tr + s, tc + s, dr, dc, s);
  45.     else{         //不在，将左上角视为特殊方块  
  46.         board[tr + s][tc + s] = t;
  47.         chessBoard(tr + s, tc + s, tr + s, tc + s, s);
  48.     }
  49. }
  50. void main(){
  51.     int size;
  52.     cout << "输入棋盘的size(大小必须是2的n次幂): ";
  53.     cin >> size;
  54.     int index_x, index_y;
  55.     cout << "输入特殊方格位置的坐标: ";
  56.     cin >> index_x >> index_y;
  57.     chessBoard(0, 0, index_x, index_y, size);
  58.              //(int tr, int tc, int dr, int dc, int size)
  59.     for (int i = 0; i < size; i++){
  60.         for (int j = 0; j < size; j++)
  61.             //cout << board[i][j] <<"/t"; //"/t输出出现问题"
  62.              printf("%d\t",board[i][j]);
  63.         cout << endl;
  64.     }
  65. }

运行结果
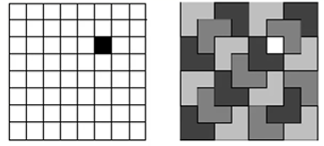
$RB9E5B9.png
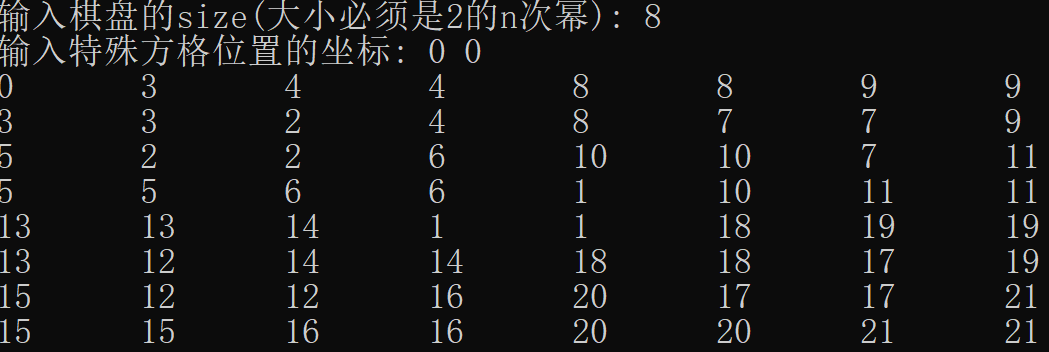
屏幕截图 2022-03-17 200830.png

#include<iostream>
using namespace std;
int tile = 1;        //L型骨牌的编号(递增)
int board[100][100];  //棋盘,设计为全局变量,初始化为0
/* 递归方式实现棋盘覆盖算法
* 输入参数：
* tr--当前棋盘左上角的行号
* tc--当前棋盘左上角的列号
* dr--当前特殊方格所在的行号
* dc--当前特殊方格所在的列号
* size：当前棋盘的:2^k     */
void chessBoard(int tr, int tc, int dr, int dc, int size){
    if (size == 1)    //棋盘方格大小为1,说明递归到最里层
        return;
    int t = tile++;     //每次递增1
    int s = size / 2;    //棋盘中间的行、列号(相等的)，用于分割棋盘

    //检查特殊方块是否在左上角子棋盘中
    if (dr < tr + s && dc < tc + s)              //在
        chessBoard(tr, tc, dr, dc, s);
    else{         //不在，将该子棋盘右下角的方块视为特殊方块
        board[tr + s - 1][tc + s - 1] = t;
        chessBoard(tr, tc, tr + s - 1, tc + s - 1, s);
    }

    //右上角子棋盘中
    if (dr < tr + s && dc >= tc + s)               //在
        chessBoard(tr, tc + s, dr, dc, s);
    else{        //不在，将该子棋盘左下角的方块视为特殊方块
        board[tr + s - 1][tc + s] = t;
        chessBoard(tr, tc + s, tr + s - 1, tc + s, s);
    }

     //左下角子棋盘中
    if (dr >= tr + s && dc < tc + s)              //在
        chessBoard(tr + s, tc, dr, dc, s);
    else{            //不在，将右上角视为特殊方块
        board[tr + s][tc + s - 1] = t;
        chessBoard(tr + s, tc, tr + s, tc + s - 1, s);
    }

    //右下角子棋盘中
    if (dr >= tr + s && dc >= tc + s)            //在
        chessBoard(tr + s, tc + s, dr, dc, s);
    else{         //不在，将左上角视为特殊方块
        board[tr + s][tc + s] = t;
        chessBoard(tr + s, tc + s, tr + s, tc + s, s);
    }
}
int main(){
    int size;
    cout << "输入棋盘的size(大小必须是2的n次幂): ";
    cin >> size;
    int index_x, index_y;
    cout << "输入特殊方格位置的坐标: ";
    cin >> index_x >> index_y;
    chessBoard(0, 0, index_x, index_y, size);
             //(int tr, int tc, int dr, int dc, int size)
    cout<<"特殊方格位置："<<"("<<index_x<<","<<index_x<<")="<<board[index_x][index_y]<<endl;
    for (int i = 0; i < size; i++){
        for (int j = 0; j < size; j++)
            //cout << board[i][j] <<"/t"; //"/t输出出现问题"
             printf("%d\t",board[i][j]);
        cout << endl;
    }
    //return 0；
}