问题描述：
n个物品组成集合O,每个商品有两个属性vi(所占体积)和pi（价格）
背包容量为C
输出商品子集S属于O,使价格最大，体积不超过背包体积

递推公式：（先上后下）

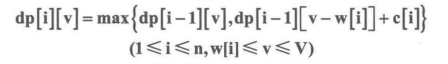
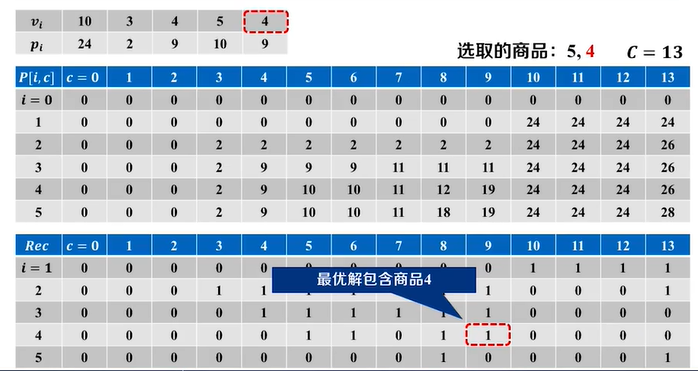
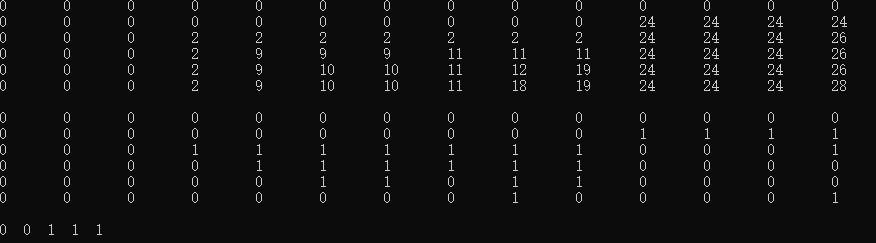
image.png
image.png

  1. #include<iostream>
  2. using namespace std;
  4. int v[] = { 0 , 10 , 3 , 4 , 5 , 4 };    //商品的体积10 , 3 , 4 , 5 , 4
  5. int p[] = { 0 , 24 , 2 , 9 , 10 , 9 };    //商品的价值24 , 2 , 9 , 10 , 9
  7. const int m = 5;                        //商品数目
  8. const int C = 13;                        //背包大小
  11. int dp[m+1][C+1] = { { 0 } };            //动态规划表  dp[i][j] i表示物品序号，j表示背包所剩空间
  12. int Rec[m+1][C+1]= { { 0 } };            //动态规划表，用于存储是否选择该商品
  13. int item[m+1];                            //最优解情况，0为未选择，1为选择
  15. void KnapsackDP() {                        //动态规划
  16.     for (int i = 0; i <= m; i++)
  17.         Rec[i][0] = dp[i][0] = 0;
  18.     for (int i = 0; i <= C; i++)
  19.         Rec[0][i] = dp[0][i] = 0;
  20.     for (int i = 1; i <= m; i++) {
  21.         for (int j = 1; j <= C; j++) {
  22.             if (j >= v[i] && dp[i - 1][j] < dp[i - 1][j - v[i]] + p[i]){
  23.                     dp[i][j] = dp[i - 1][j - v[i]] + p[i];
  24.                                         //构造dp数组，包中装入第i个商品
  25.                     Rec[i][j] = 1;        //选则了第i个        
  26.             }
  27.             else {
  28.                 dp[i][j] = dp[i - 1][j];//最优解向下瞬移
  29.                 Rec[i][j] = 0;            //第i个未被选择
  31.             //if (j >= v[i]) {
  32.             //    if (dp[i - 1][j] < dp[i - 1][j - v[i]] + p[i]){
  33.             //        dp[i][j] = dp[i - 1][j - v[i]] + p[i];
  34.             //                            //构造dp数组，包中装入第i个商品
  35.             //        Rec[i][j] = 1;        //选则了第i个        
  36.             //    }
  37.             //    else {        
  38.             //        dp[i][j] = dp[i - 1][j];
  39.             //        Rec[i][j] = 0;            //第i个未被选择
  40.             //    }
  41.             //}
  42.             //else {
  43.             //    dp[i][j] = dp[i - 1][j];
  44.             //    Rec[i][j] = 0;
  45.             }    
  46.         }
  47.     }
  48. }
  50. void IsSelect(int i, int j) {            //解析最优解
  51.     if (i > 0) {
  52.         if (Rec[i][j]>0) {
  53.             item[i] = 1;
  54.         }
  55.         else
  56.             item[i] = 0;
  57.         IsSelect(i - 1, j - v[i]);
  58.     }
  59. }
  61. void Print() {
  62.     for (int i = 0; i <= m; i++) {        //输出dp数组
  63.         for (int j = 0; j <= C; j++) {
  64.             cout << dp[i][j] << "\t";
  65.         }
  66.         cout << endl;
  67.     }
  68.     cout << endl;
  70.     for (int i = 0; i <= m; i++) {        //输出Rec数组
  71.         for (int j = 0; j <= C; j++) {
  72.             cout << Rec[i][j] << "\t";
  73.         }
  74.         cout << endl;
  75.     }
  76.     cout << endl;
  78.     for (int i = 1; i <= m; i++)
  79.         cout << item[i] << "  ";
  80.     cout << endl;
  81. }
  83. int main()
  84. {
  85.     KnapsackDP();
  86.     IsSelect(m, C);
  87.     Print();
  88.     return 0;
  89. }

运行结果：
image.png