问题描述：

给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?
0-1背包问题是一个特殊的整数规划问题。

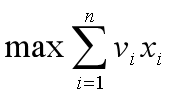
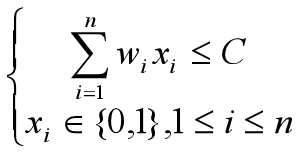
image.pngimage.png
0-1背包问题的子问题最优值为m(i，j)，即m(i，j)是背包容量为j，可选择物品为i，i+1，…，n时0-1背包问题的最优值。由0-1背包问题的最优子结构性质，可以建立计算m(i，j)的递归式如下。（先下后上）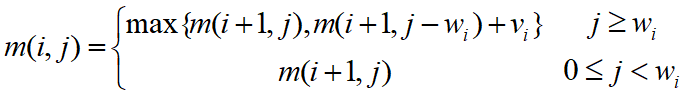
image.png

算法复杂度分析

从m(i，j)的递归式容易看出，算法需要O(nc)计算时间。当背包容量c很大时，算法需要的计算时间较多。例如，当c>2n时，算法需要Ω(n2n)计算时间。

例：

n=5,c=10,w={2,2,6,5,4},v={6,3,5,4,6}
image.png

  1. void Knapsack(int v[], int w[], int c, int n, int m[][11]) {
  2.     int jMax = (w[n] - 1) > c ? c : (w[n] - 1);
  4.     for (int j = 0; j <= c; j++)
  5.         m[n][j] = 0;                        //前两个for用于构造m[i][j]数组的最后一行
  6.     for (int j = w[n]; j <= c; j++)
  7.         m[n][j] = v[n];                        //当动态背包容量j大于时，最后一个商品既可以放入背包
  9.     for (int i = n - 1; i >= 1; i--) {
  10.         int jMax = (w[i] - 1> c) ? c : (w[i] - 1);
  11.         for (int j = 0; j <= jMax; j++)
  12.             m[i][j] = m[i+1][j];
  13.         for (int j = w[i]; j <= c; j++)
  14.             m[i][j] = (m[i + 1][j] > (m[i + 1][j - w[i]] + v[i])) ? m[i + 1][j] : (m[i + 1][j - w[i]] + v[i]);
  15.     }
  16.     /*
  17.     m[1][c] = m[2][c];//可以没有
  18.     if(c>=w[1])
  19.         m[1][c]= m[1][c] > (m[2][c - w[1]] + v[1]) ? m[1][c] : (m[2][c - w[1]] + v[1]);
  20.     */
  21. }
  23. void Traceback(int m[][11], int w[], int c, int n, int x[]) {
  25.     for (int i = 1; i < n; i++)
  26.     {
  27.         if (m[i][c] == m[i + 1][c])
  28.             x[i] = 0;
  29.         else {
  30.             x[i] = 1;
  31.             c -= w[i];                        //选择第i个商品之后，背包容量减小w[i]
  32.         }
  33.         x[n] = (m[n][c]) ? 1 : 0;            //判断是否选择了最后一个商品
  34.     }
  35. }
  1. #include<iostream>
  2. using namespace std;
  4. void Knapsack(int v[], int w[], int c, int n, int m[][11]) {
  5.     int jMax = (w[n] - 1) > c ? c : (w[n] - 1);
  7.     for (int j = 0; j <= c; j++)
  8.         m[n][j] = 0;                        //前两个for用于构造m[i][j]数组的最后一行
  9.     for (int j = w[n]; j <= c; j++)
  10.         m[n][j] = v[n];                        //当动态背包容量j大于时，最后一个商品既可以放入背包
  12.     for (int i = n - 1; i >= 1; i--) {
  13.         int jMax = (w[i] - 1> c) ? c : (w[i] - 1);
  14.         for (int j = 0; j <= jMax; j++)
  15.             m[i][j] = m[i+1][j];
  16.         for (int j = w[i]; j <= c; j++)
  17.             m[i][j] = (m[i + 1][j] > (m[i + 1][j - w[i]] + v[i])) ? m[i + 1][j] : (m[i + 1][j - w[i]] + v[i]);
  18.     }
  19.     /*
  20.     m[1][c] = m[2][c];//可以没有
  21.     if(c>=w[1])
  22.         m[1][c]= m[1][c] > (m[2][c - w[1]] + v[1]) ? m[1][c] : (m[2][c - w[1]] + v[1]);
  23.     */
  24. }
  26. void Traceback(int m[][11], int w[], int c, int n, int x[]) {
  28.     for (int i = 1; i < n; i++)
  29.     {
  30.         if (m[i][c] == m[i + 1][c])
  31.             x[i] = 0;
  32.         else {
  33.             x[i] = 1;
  34.             c -= w[i];                        //选择第i个商品之后，背包容量减小w[i]
  35.         }
  36.         x[n] = (m[n][c]) ? 1 : 0;            //判断是否选择了最后一个商品
  37.     }
  38. }
  40. int main() {
  41.     int w[] = { 0,2,2,6,5,4 };        //商品的体积10 , 3 , 4 , 5 , 4
  42.     int v[] = { 0,6,3,5,4,6 };        //商品的价值24 , 2 , 9 , 10 , 9
  43.     const int n = 5, c = 10;        //商品个数，背包大小
  45.     int m[n + 1][c + 1];                //动态规划数组
  46.     int item[n + 1]={0};                //商品序列
  48.     Knapsack(v, w, c, n, m);            //构造dp数组
  49.     Traceback(m, w, c, n, item);        //解析最优选择
  51.     for (int i = 1; i <= n; i++) {        //输出dp数组
  52.         for (int j = 1; j <= c; j++) {
  53.             cout << m[i][j] << " ";
  54.         }
  55.         cout << endl;
  56.     }
  57.     cout << endl;
  59.     for (int j = 1; j <= n; j++) {        //输出最优数组
  60.         if (item[j] > 0)
  61.             cout << "装入商品： " << j << endl;
  62.     }
  63.     cout << "装入背包最大价值为：" << m[1][c] << " 元\n";
  65.     return 0;
  66. }

运行结果：
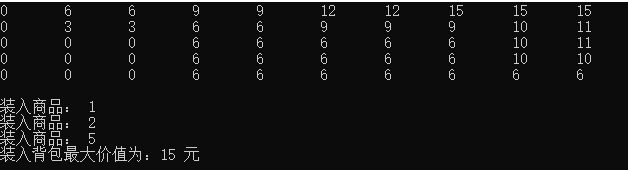
image.png

优化：

#include<iostream>
using namespace std;

void Knapsack(int v[], int w[], int c, int n, int m[][11]) {

    for (int j = 0; j <= c; j++)
        m[n+1][j] = 0;

    for (int i = n; i >= 1; i--) {
        for (int j = 0; j <= c; j++){
            if(j<w[i])
                m[i][j]= m[i + 1][j];
            else
                m[i][j] = (m[i + 1][j] > (m[i + 1][j - w[i]] + v[i])) ? m[i + 1][j] : (m[i + 1][j - w[i]] + v[i]);
        }    
    }
}

void Traceback(int m[][11], int w[], int c, int n, int x[]) {

    for (int i = 1; i < n; i++)
    {
        if (m[i][c] == m[i + 1][c])
            x[i] = 0;
        else {
            x[i] = 1;
            c -= w[i];                        //选择第i个商品之后，背包容量减小w[i]
        }
        x[n] = (m[n][c]) ? 1 : 0;            //判断是否选择了最后一个商品
    }
}

int main() {
    int w[] = { 0,2,2,6,5,4 };        //商品的体积10 , 3 , 4 , 5 , 4
    int v[] = { 0,6,3,5,4,6 };        //商品的价值24 , 2 , 9 , 10 , 9
    const int n = 5, c = 10;        //商品个数，背包大小

    int m[n + 2][c + 1];            //动态规划数组<多加一行的辅助空间，全部初始化为0>
    int item[n + 1] = { 0 };            //商品序列

    Knapsack(v, w, c, n, m);        //构造dp数组
    Traceback(m, w, c, n, item);    //解析最优选择

    for (int i = 1; i <= n; i++) {    //输出dp数组
        for (int j = 1; j <= c; j++) {
            cout << m[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;

    for (int j = 1; j <= n; j++) {        //输出最优数组
        if (item[j] > 0)
            cout << "装入商品： " << j << endl;
    }
    cout << "装入背包最大价值为：" << m[1][c] << " 元\n";

    return 0;
}