时间复杂性分析

快速排序（Quicksort）是对冒泡排序的一种改进。
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
快速排序算法是基于分治策略的另一种排序算法。其基本思想是，对于输入的子数组a[p,r],按以下三个步骤进行排序。
（1）分解(Divide) 以a[p] 为基准元素将a[p:r]划分为3段a[p:q-1],a[q],和a[q+1:r]。使a[p:q-1]中的任一元素小于a[q],而a[q+1:r]中的任一元素大于a[q]。下标q在划分中确定。
（2）递归求解(Conquer):通过递归调用快速算法分别对a[p,q-1]和a[q+1,r]进行排序。
（3）不需要再进行合并排序，当递归调用排序后，a[p:r]就已排好序。

时间复杂性分析

最坏情形：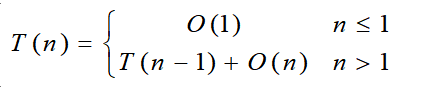
解此递归方程可得T(n)=O(n2)。
最好情形：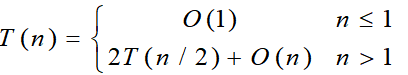
解此递归方程可得T(n)=O(nlogn)。

template<class Type>
void QuickSort(Type a[], int p, int r)
{
    if (p<r) 
    {
        int q=Partition(a,p,r);
        QuickSort (a,p,q-1);         空    //对左半段排序
        QuickSort (a,q+1,r);         空    //对右半段排序
    }
}

#include<iostream>
using namespace std;
#define N 10
template<class Type>
int Partition(Type a[], int p, int r) {
    int i = p, j = r + 1;
    Type x = a[p];//存放待排数组左边数字
    while (true){
        while (a[++i] < x && i < r);//前往后找到大于x的数
        while (a[--j] > x);//后往前找到小于x的数
        if (i >= j)
            break;
        swap(a[i], a[j]);
    }
    a[p] = a[j];
    cout <<j<<" "<< a[j] << endl;
    a[j] = x;
    return j;//此时j的左边比a[j]小，右边比a[j]大
}
template<class Type>
void QuickSort(Type a[], int p, int r) {
    if (p < r){
        int q = Partition(a, p, r);//此时q的左边比a[q]小，右边比a[q]大
        QuickSort(a, p, q - 1);//递归排序左边
        QuickSort(a, q + 1, r);//右边
    }
}
template<class Type>
void Print(Type a[]) {
    for(int i=0;i<N;i++)
        cout << a[i] << " ";
    cout << endl;
}
int main() {
    int a[N];
    for (int i = 0; i <N ; i++)
        a[i] = rand() % N + 1;
    int i = N;
    Print(a);
    QuickSort(a, 0, N-1);//升序
    Print(a);
    return 0;
}

一些改进方法：
快速排序算法的性能取决于划分的对称性，通过修改函数Partition,,可以设计出采用随机选择策略的快速排序算法。
快速排序的最坏情况基于每次划分对主元的选择。基本的快速排序选取第一个元素作为主元。这样在数组已经有序的情况下，每次划分将得到最坏的结果。一种比较常见的优化方法是随机化算法，即随机选取一个元素作为主元。这种情况下虽然最坏情况仍然是O(n^2)，但最坏情况不再依赖于输入数据，而是由于随机函数取值不佳。实际上，随机化快速排序得到理论最坏情况的可能性仅为1/(2^n)。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn)的期望时间复杂度。一位前辈做出了一个精辟的总结：“随机化快速排序可以满足一个人一辈子的人品需求。”
随机化快速排序的唯一缺点在于，一旦输入数据中有很多的相同数据，随机化的效果将直接减弱。对于极限情况，即对于n个相同的数排序，随机化快速排序的时间复杂度将毫无疑问的降低到O(n^2)。解决方法是用一种方法进行扫描，使没有交换的情况下主元保留在原位置。

#include<iostream>
using namespace std;
#define N 20
template<class Type>
void Print(Type a[]) {
    for(int i=0;i<N;i++)
        cout << a[i] << " ";
    cout << endl;
}
template<class Type>
int Partition(Type a[], int p, int r) {
    int i = p, j = r + 1;
    Type x = a[p];//存放待排数组左边数字
    while (true){
        while (a[++i] < x && i < r);//前往后找到大于x的数
        while (a[--j] > x);//后往前找到小于x的数
        if (i >= j)
            break;
        swap(a[i], a[j]);
    }
    a[p] = a[j];
    //cout <<j<<" "<< a[j] << endl;
    a[j] = x;
    return j;//此时j的左边比a[j]小，右边比a[j]大
}
template<class Type>
void QuickSort(Type a[], int p, int r) {
    if (p < r){
        int q = Partition(a, p, r);//此时q的左边比a[q]小，右边比a[q]大
        printf("%d\t%d\t",q,a[q]);
        //cout<<q<<" " <<a[q]<<"      ";
        Print(a);
        QuickSort(a, p, q - 1);//递归排序左边
        QuickSort(a, q + 1, r);//右边
    }
}
int main() {
    int a[N];
    for (int i = 0; i <N ; i++)
        a[i] = rand() % N + 1;
    //int i = N;
    printf("随机生成数:\t");
    Print(a);
    QuickSort(a, 0, N-1);//升序
    printf("排序后:\t\t");
    Print(a);
    return 0;
}

快排

时间复杂性分析