关于图的几个概念定义

  • 连通图：在无向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该无向图为连通图。
  • 强连通图：在有向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该有向图为强连通图。
  • 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接每个顶点的代价，称这种连通图叫做连通网。
  • 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
  • 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

最小生成树（Minimum Spanning Tree,MST）

问题描述

设G =(V,E)是无向连通带权图，即一个网络。E中每条边(v,w)的权为c[v][w]。如果G的子图G’是一棵包含G的所有顶点的树，则称G’为G的生成树。生成树上各边权的总和称为该生成树的耗费。在G的所有生成树中，耗费最小的生成树称为G的最小生成树。

最小生成树性质

用贪心算法设计策略可以设计出构造最小生成树的有效算法。本节介绍的构造最小生成树的Prim算法和Kruskal算法都可以看作是应用贪心算法设计策略的例子。尽管这2个算法做贪心选择的方式不同，它们都利用了下面的最小生成树性质（MST）
设G=(V,E)是连通带权图，U是V的真子集。如果(u,v)属于E，且u属于U，v属于V-U，且在所有这样的边中，(u,v)的权c[u][v]最小，那么一定存在G的一棵最小生成树，它以(u,v)为其中一条边。这个性质有时也称为MST性质。
注：最小生成树可以不唯一，但是边权之和是唯一的（题目中涉及到最小生成树的输出，为了让最小生成树唯一，一般都会给出根节点）

1、Prim算法

注：Prim算法和Dijkstra算法的思想完全相同，算法相似稍微有点区别。
设G=(V,E)是连通带权图，V={1,2,…,n}。
构造G的最小生成树的Prim算法的基本思想是：首先置S={1}，然后，只要S是V的真子集，就作如下的贪心选择：选取满足条件i属于S，j属于V-S，且c[i][j]最小的边，将顶点j添加到S中。这个过程一直进行到S=V时为止。
在这个过程中选取到的所有边恰好构成G的一棵最小生成树。
利用最小生成树性质和数学归纳法容易证明，上述算法中的边集合T始终包含G的某棵最小生成树中的边。因此，在算法结束时，T中的所有边构成G的一棵最小生成树。
例如，对于图中的带权图，按Prim算法选取边的过程如下页图所示。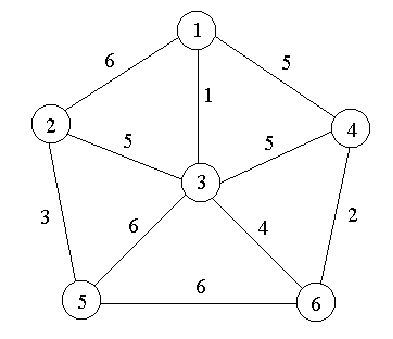
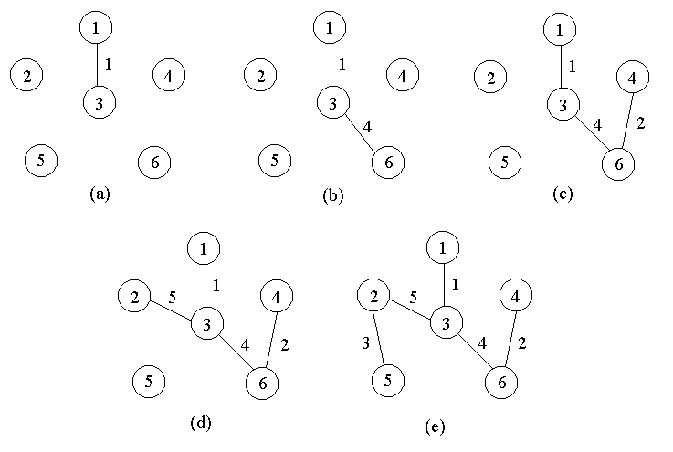
image.png
image.png
在上述Prim算法中，还应当考虑如何有效地找出满足条件image.png，且权c[i][j]最小的边(i,j)。实现这个目的的较简单的办法是设置2个数组closest和lowcost。
在Prim算法执行过程中，先找出V-S中使lowcost值最小的顶点j，然后根据数组closest选取边(j,closest[j］)，最后将j添加到S中，并对closest和lowcost作必要的修改。
用这个办法实现的Prim算法所需的计算时间为 O(n**2**)

  1. void Prim(int n, int c[][20])//规定从1出发,求出根节点为1的最小生成树
  2. {
  3.     bool s[MAX];        //记录第i个节点是否加入最小生成树集合
  4.     int lowcost[20];    //记录节点间的权值
  5.     int closest[20];    //记录上一个节点
  7.     for (int i = 0; i <= n; i++)
  8.     {
  9.         lowcost[i] = c[1][i]; //记录当前节点到各个节点的权值（这里是根节点）
  10.         closest[i] = 1;       //closest[i] = j,表示i的前一个节点是j，即closest[i]-->i
  11.         s[i] = false;         //s[i]=true表示第i个节点加入到最小生成树中
  12.     }
  13.     s[1] = true;
  15.     for (int i = 1; i < n; i++)
  16.     {
  17.         int min = inf;//初始化无穷大
  18.         int j = 1;
  19.         for (int k = 2; k <= n; k++)
  20.             if ((lowcost[k] < min) && (!s[k])) 
  21.             {                  //搜索最小值，V-S中使lowcost值最小的顶点j
  22.                 min = lowcost[k];
  23.                 j = k;
  24.             }
  26.         cout << closest[j] << "-->" << j << "  权值：" << lowcost[j] << endl;
  27.         s[j] = true;
  29.         for (int k = 2; k <= n; k++)
  30.             if ((c[j][k] < lowcost[k]) && (!s[k]))
  31.             {                    //判断新加入节点后,到剩余节点的权值是否会更小
  32.                 lowcost[k] = c[j][k];
  33.                 closest[k] = j;
  34.             }
  35.     }
  36. }
#include<iostream>
using namespace std;
#define MAX 100
#define inf 0x7fffffff

int prim(int n, int c[][20])//规定从1出发,求出根节点为1的最小生成树
{
    bool s[MAX];//记录第i个节点是否加入最小生成树集合
    int lowcost[20], closest[20];
    s[1] = true;
    int sum = 0;    //记录最小权值之和，后返回最小值

    for (int i = 0; i <= n; i++)
    {
        lowcost[i] = c[1][i];   //记录当前节点到各个节点的权值（这里是根节点）
        closest[i] = 1;         //closest[i] = j,表示i的前一个节点是j，即closest[i]-->i
        s[i] = false;           //s[i]=true表示第i个节点加入到最小生成树中
    }

    for (int i = 1; i < n; i++)
    {
        int min = inf;//初始化无穷大
        int j = 1;
        for (int k = 2; k <= n; k++)
            if ((lowcost[k] < min) && (!s[k])) //搜索最小值，V-S中使lowcost值最小的顶点j
            { 
                min = lowcost[k]; 
                j = k; 
            }

        cout << closest[j] << "-->" << j << "  权值：" << lowcost[j] << endl;
        sum += lowcost[j];
        s[j] = true;

        for (int k = 2; k <= n; k++)
            if ((c[j][k] < lowcost[k]) && (!s[k]))//判断新加入节点后,到剩余节点的权值是否会更小
            {
                lowcost[k] = c[j][k];
                closest[k] = j;
            }
    }
    return sum;
}


int main() {
    int graph[20][20];
    cout << "输入顶点个数和边的个数\n";
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)//初始化，边为无穷大则不联通
        for (int j = 1; j <= n; j++)
            graph[i][j] = inf;

    for (int k = 1; k <= m; k++)//构建图
    {
        int i, j, w;
        cin >> i >> j >> w;
        graph[i][j] = graph[j][i] = w;
    }

    int mincost = prim(n, graph);//求解最小值
    cout << "最小权值和为：" << mincost << endl;

    return 0;
}

测试数据
6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6
运行结果：
1—>3 权值：1
3—>6 权值：4
6—>4 权值：2
3—>2 权值：5
2—>5 权值：3
最小权值和为：15

2、Kruskal算法

基本思想

  • 将所有的边按权从小到大排序,依边权递增的顺序查看每一条边。
  • 连接2个不同的连通分支：
    1. 当查看到第k条边(v,w)时，如果端点v和w分别是当前2个不同的连通分支T1和T2中的顶点时，就用边(v,w)将T1和T2连接成一个连通分支。
1. 继续查看第k+1条边：如果端点v和w在当前的同一个连通分支中，就直接再查看第k+1条边。这个过程一直进行到只剩下一个连通分支时为止。

例如，对前面的连通带权图，按Kruskal算法顺序得到的最小生成树上的边如下图所示。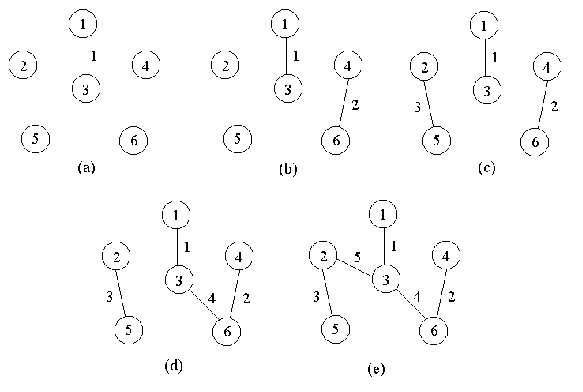
image.png
按权的递增顺序查看等价于对结构体数组S依权排序。
对一个由连通分支组成的集合不断进行修改，用数组X[i]的值表示i所在的分支。
当图的边数为e时，Kruskal算法所需的计算时是 O(eloge)。当e=O(n**2**)时，Kruskal算法比Prim算法差，但当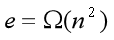image.png时，Kruskal算法却比Prim算法好得多。
Krusal算法实现的时间主要用于对边的排序，所以时间复杂度为：O(nlogn)

具体流程

(1)将图G看做一个森林，每个顶点为一棵独立的树
(2)将所有的边加入集合S，即一开始S = E
(3)从S中拿出一条最短的边(u,v)，如果(u,v)不在同一棵树内，则连接u,v合并这两棵树，同时将(u,v)加入生成树的边集E’
(4)重复(3)直到所有点属于同一棵树，边集E’就是一棵最小生成树

struct edgenode
{    
    int weight;
    int u,v; 
}

int find(int  x[],int m)
{
    return x[m]; 
}

void kruskal(edgenode s[],int n)
{        
    int k=0; int a,b;

    while(n) 
    {   
        a=find(x,s[k].u); 
        b=find(x,s[k].v);
        if(a!=b)
        { 
            for(int i=1;i<7;i++) 
                if(x[i]==a)
                    x[i]=b;
             cout<<"("<<s[k].u<<","<<s[k].v<<")"<<s[k].weight<<endl；
        } 
        k++; 
        n--; 
    }
}

void kruskal(int n, int m)    //n为顶点个数，m为图的边数
{        //（这里假设边集合已经按权值的升序排好列）
    int ans = 0;            //边权之和
    int Num_Edge = 0;        //当前生成树的边数

    int visited[100];//并查数组
    for (int i = 0; i < n; i++)    //顶点范围[0，n-1]
        visited[i] = i;            //初始化

    sort(E, E + m, cmp);        //cmp为仿函数，按照weight的升序排列

    for (int i = 0; i < m; i++)    //枚举所有的边
    {
        int a = visited[E[i].u];//查询测试两边两个端点所在集合的根节点
        int b = visited[E[i].v];S

        if (a != b)                //不在一个集合中
        {
            for (int i = 0; i <= n; i++)
            {            //路径压缩,合并集合（把测试边加入最小生成树中）
                if (visited[i] == b)
                    visited[i] = a;    //加入后的顶点的根节点都为a
            }
            ans += E[i].weight;        //边权之和增加测试边的边权
            Num_Edge++;                //当前生成树的边数加1
        }
    }
}

#include<iostream>
#include<algorithm>//标准算法头文件
using namespace std;

struct edge {
    int u, v;//边的两端编号
    int weight;
}E[1000];//最大边数

int visited[100];//并查数组

bool cmp(edge a, edge b)
{
    return a.weight < b.weight;
}

int kruskal(int n, int m)    //n为顶点个数，m为图的边数
{
    int ans = 0;            //边权之和
    int Num_Edge = 0;        //当前生成树的边数

    for (int i = 0; i < n; i++)    //顶点范围[0，n-1]
        visited[i] = i;            //初始化

    sort(E, E + m, cmp);        //cmp为仿函数，按照weight的升序排列

    /*for (int i = 0; i < m; ++i)//输出排序后的边集合
        cout << E[i].u << " " << E[i].v << " " << E[i].weight << endl;*/

    for (int i = 0; i < m; i++)    //枚举所有的边
    {
        int a = visited[E[i].u];//查询测试两边两个端点所在集合的根节点
        int b = visited[E[i].v];

        if (a != b)                //不在一个集合中
        {
            for (int i = 0; i <= n; i++)
            {            //路径压缩,合并集合（把测试边加入最小生成树中）
                if (visited[i] == b)
                    visited[i] = a;    //加入后的顶点的根节点都为a
            }
            ans += E[i].weight;        //边权之和增加测试边的边权
            Num_Edge++;                //当前生成树的边数加1
            if (Num_Edge == n - 1)    //变数等于顶点数减1结束
                break;
        }
    }
    if (Num_Edge != n - 1)            //无法连通时返回-1
        return -1;
    else
        return ans;                    //返回最小生成树边权之和
}

int main()
{
    int n, m;//顶点，边数
    cin >> n >> m;

    for (int i = 0; i < m; ++i)
        cin >> E[i].u >> E[i].v >> E[i].weight;

    int ans = kruskal(n, m);
    printf("%d\n", ans);
    return 0;
}

测试数据：
6 10
0 1 4
0 4 1
0 5 2
1 2 1
1 5 3
2 3 6
2 5 5
3 4 5
3 5 4
4 5 3
运行结果：11
代码测试运行分析：
边集合排列后输出:（按照升序）
0 4 1
1 2 1
0 5 2
1 5 3
4 5 3
0 1 4
3 5 4
2 5 5
3 4 5
2 3 6
visited数组每次输出：
0 1 2 3 4 5
0 1 2 3 0 5
0 1 1 3 0 5
0 1 1 3 0 0
1 1 1 3 1 1//这三行未变化说明该边已经加入到最小生成树中
1 1 1 3 1 1
1 1 1 3 1 1
3 3 3 3 3 3