递归典型问题

全排列
整数划分
汉诺塔问题

分治典型问题

二分搜索算法
大整数的乘法
棋盘覆盖
循环赛日程表
Strassen矩阵乘法
合并排序
快速排序

问题：

1、实现大整数的乘法是利用的算法（ C ）。
A、贪心法 B、动态规划法 C、分治策略 D、回溯法
2、二分搜索算法是利用（ A ）实现的算法。
A、分治策略 B、动态规划法 C、贪心法 D、回溯法
3、以下不可以使用分治法求解的是（D ）。
A 棋盘覆盖问题 B 选择问题 C 归并排序 D 0/1背包问题
4、实现循环赛日程表利用的算法是（ A ）。
A、分治策略 B、动态规划法 C、贪心法 D、回溯法
5、实现棋盘覆盖算法利用的算法是（ A ）。
A、分治法 B、动态规划法 C、贪心法 D、回溯法
6、Strassen矩阵乘法是利用（ A ）实现的算法。
A、分治策略 B、动态规划法 C、贪心法 D、回溯法
7、使用分治法求解不需要满足的条件是（A ）。
A 子问题必须是一样的
B 子问题不能够重复
C 子问题的解可以合并
D 原问题和子问题使用相同的方法解
8、实现合并排序利用的算法是（ A ）。
A、分治策略 B、动态规划法 C、贪心法 D、回溯法
9、快速排序算法是基于 ** 分治策略 ** 的一种排序算法。
10、从分治法的一般设计模式可以看出，用它设计出的程序一般是递归算法
11、分治法的基本思想是：分解求解合并（详细）
将一个规模为n的问题分解为k个规模较小的子问题，这些子问题互相独立且与原问题相同。递归地解这些子问题，然后将各个子问题的解合并得到原问题的解。
12、分治法的基本步骤：分解、递归求解、合并
分治法在每一层递归上都有三个步骤：
（1）分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；（分解为小规模问题）
（2）递归求解：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题；（直接求解或递归解决）
（3）合并：将各个子问题的解合并为原问题的解。（合并子问题解）
13、分治法与动态规划法
相同点是：将待求解的问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
两者的不同点是：适合于用动态规划法求解的问题，经分解得到的子问题往往不是互相独立的。而用分治法求解的问题，经分解得到的子问题往往是互相独立的。
14、分治法所能解决的问题一般具有以下几个特征：
（1）该问题的规模缩小到一定的程度就可以容易地解决；
（2）该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；
（3）利用该问题分解出的子问题的解可以合并为该问题的解；
（4）该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

15、 请用分治策略设计递归的归并排序算法，并分析其时间复杂性（要求：分别给出divide、conquer、combine这三个阶段所花的时间，并在此基础上列出递归方程，最后用套用公式法求出其解的渐进阶）。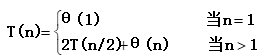
image.png

  1. Template <class Type>
  2. void MergeSort (Type a[ ], int left, int right)     
  3. { 
  4.     if (left<right)                            
  5.     { 
  6.         int i=（left+right）/2;               
  7.         MergeSort（a, left, i）;               
  8.         MergeSort（a, i+1, right）;            
  9.         Merge(a, b, left, right);               
  10.         Copy(a, b, left, right);                 
  11.      }
  12. }
  13. Divide 阶段的时间复杂性：   O(1)          
  14. Conquer阶段的时间复杂性：  2T(n)          
  15. Combine阶段的时间复杂性： Θ(n)          
  16. 用套用公式法：a=2, b=2, nlog ba = n , f(n)=n,   因为f(n)与nlog ba 同阶，
  17. ∴T(n) =Θ(nlogn)

16、考虑在序列A[1..n]中找最大最小元素的问题。一个分治算法描述如下：如果n≤2 就直接求解。否则，将序列等分成两个子序列A[1..n/2]和A[n/2+1..n]，分别找出这两子序列的最大最小元素x1,y1 和x2,y2；然后据此求出A[1..n]的最大元素x=max{x1,x2}及最小元素y=min{y1,y2}。请给出该算法计算时间T(n)满足的递归方程，并解方程来确定算法的时间复杂度。假定n=2k（k 为正整数）。
答：
算法时间复杂度满足如下递归方程：
T(n)=2T(n/2)+2（n>2）；T(2)=1。
因为n=2 k（k 为正整数），所以，
T(n)= T(2 _k)= 2T(2 k-1)+2
= 22T(2 k-2)+ 22+2
⋯
= 2k-1T(2)+ 2k-2+⋯+23+22+2
= 2k-1+⋯+23+22+2。因此，_T(n)=O(n)。

  1. Template <class Type>
  2. void perm(Type list[],  int k, int m )    //产生[list[k:m]的所有排列
  3. {
  4.     if(k==m)                                空
  5.     {  //只剩下一个元素
  6.         for (int i=0;i<=m;i++)  
  7.             cout<<list[i];
  8.         cout<<endl;
  9.     }
  10.     else  //还有多个元素待排列，递归产生排列
  11.         for (int i=k; i<=m; i++)            空
  12.         {
  13.             swap(list[k]，list[i]);
  14.             perm(list,k+1;m);                空
  15.             swap(list[k],list[i]);         
  16.         }
  17. }
template<class Type>
void QuickSort (Type a[], int p, int r)
{
    if (p<r) 
    {
        int q=Partition(a,p,r);
        QuickSort (a,p,q-1);         空    //对左半段排序
        QuickSort (a,q+1,r);         空    //对右半段排序
    }
}

template<class Type> 
int BinarySearch(Type a[], const Type& x, int l, int r)
{
    while (l<=r)                空
    { 
        int m = ((l+r)/2);        空
        if (x == a[m]) 
            return m;
        if (x < a[m])             空
            r = m-1; 
        else 
            l = m+1;
    }
    return -1;
}

template<class Type>
void Mergesort(Type a[ ], int left, int right)
{
    if (left<right)                    空
    {
        int i=( left+right)/2;        空
        Mergesort(a, left, i );
        Mergesort(a, i+1, right);    空
        Merge(a,b, left,i,right);//合并到数组b
        Copy(a,b, left,right ); //复制到数组a
    }
}

int  power ( x, m )//计算x^m的值并返回。
{
    y=1;            空
    i=m;
    While(i-->0)    空
       y=y*x;
    return y;        空
}