引言

我们知道，在二元函数积分中，积分值不仅与曲线的端点有关，还和积分的曲线路径有关，下面将给出，什么条件在，复变函数的积分只与端点有关，和积分路劲无关。为此，需要给出区域的概念

单通区域与复通区域

定义

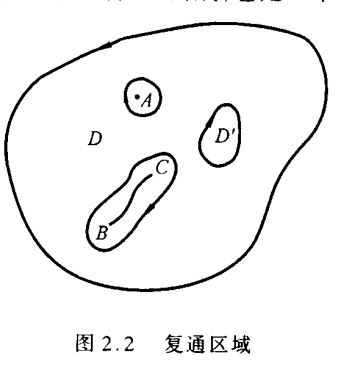
对于一个区域D,如果D内的任何闭合曲线在收缩为一点的过程中，曲线上的所有点都在D内，则称D为单通区域，否则称为复通区域。例如图2.2，最外面的曲线边界组成的是单通区域，如果加上里面的几条边界线，那就是复通区域。

区域边界线正方向的定义

沿着边界线走，区域一直在左侧。

柯西定理一

:::info 设是由境界线 组成的单通区域上的解析函数，那么：
::: :::tips 推论一
在单通区域内，解析函数的积分只与起点端点位置有关，与曲线路劲无关。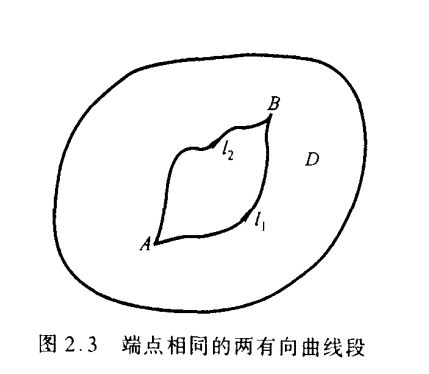

:::

柯西定理二

:::info 设为复通区域上的全部境界线，取正方向，是区域上的解析函数，则：

::: :::tips 推论一
对于闭复通区域上的单值解析函数，其外部境界线逆时针方向的积分等于内部境界线的逆时针积分之和，
推论二 重要
设是闭区域（单通或者复通）上的解析函数，内一条封闭曲线可以在区域内随便变形，而积分值保持不变。 :::