序

线弹性断裂力学中，在裂纹尖端出现无穷大的应力，这在实际中是不可能的，所以在实际中，裂纹尖端必然会出现一定范围的塑性区，当塑性区范围较小的时候，可以通过对弹性断裂力学的修正来处理计算，但当出现大范围屈服的时候，弹性断裂力学的理论不再适用。
那么，需要将塑形考虑进来，弹塑性断裂力学的任务，是找到在弹塑性场（应力场、应变场、位移场）下，裂纹附近的合适的物理量，可以度量出场的强度。
本章主要建立了两种度量的物理量，一种是裂纹尖端张开位移（CTOD），一种是J积分。

Irwin对裂纹尖端塑性区的估计及小范围屈服时塑性区的修正

Irwin对塑性区的范围进行了估计。
I型裂纹，根据应力公式计算主应力

屈服准则为Mises屈服准则

将(5.1.2)代入(5.1.1)可以得到塑性区的边界方程，以裂尖为原点的极坐标方程。

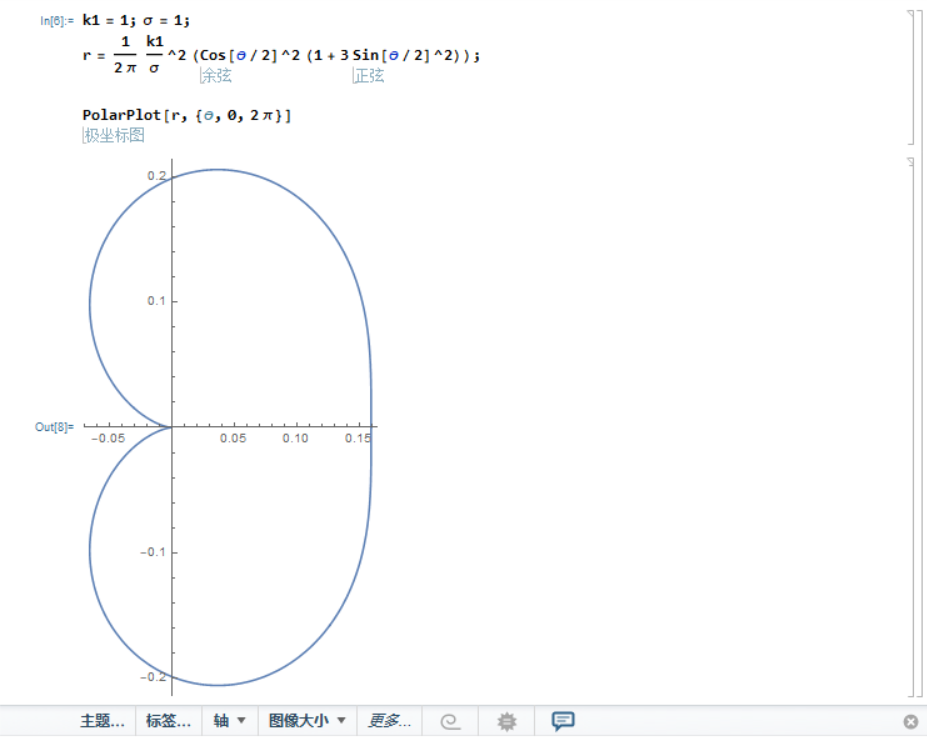:::info 时刻留意计算的假定
在上述计算中，应力的公式是完全基于弹性力学得到的，也就是说假定了裂尖的应力分布为弹性的分布，是为了简化计算，然后需要对比计算结果进行修正。 :::
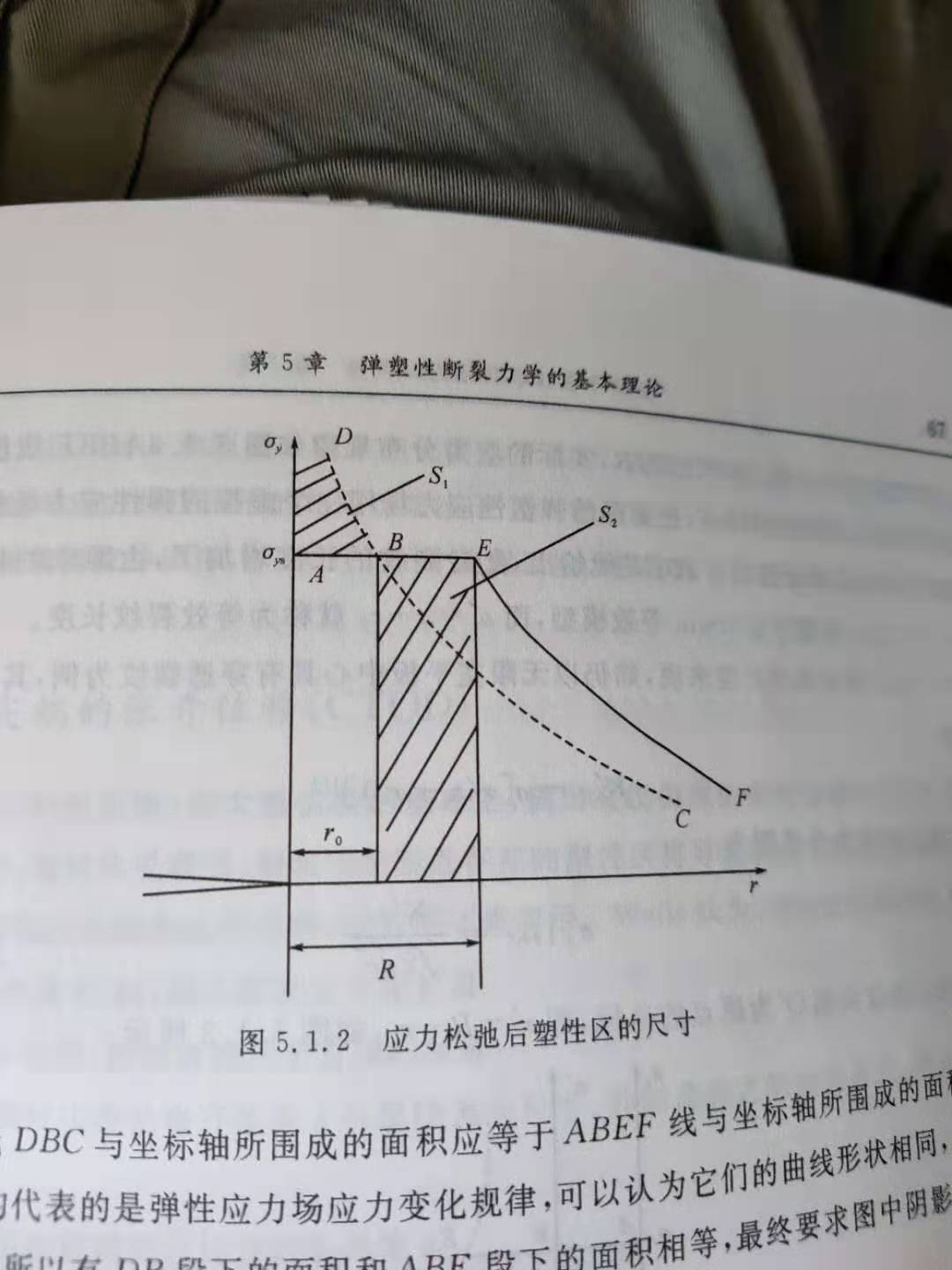
弹性假定下，应力分布随半径的变化曲线为虚线DBC，但是实际按照理想塑形模型，塑性区内的应力应该是AB段的直线，那么按照截面的力平衡条件（及应力积分应该等于外力，也就是虚线下围成的面积应该等于实线下围成的面积），那么塑性区应该扩大，其中是上述弹性理论计算的塑性区半径，接下来就是利用微积分来分析按照力平衡等效后实际的塑性区半径。 :::tips 技巧：曲线面积相等，刨除掉公共面积，就是面积DBA等于面积BEFC，而EF和BC假定为平行的，也就是不影响塑性区外的应力分布，考虑到平行四边形的面积计算公式，那么BEFC面积等于阴影所示长方形的面积。也就是两个阴影面积相等。 ::: :::danger 此处书上的计算公式与文字叙述的不匹配，个人理解应该是，不过按照书上的来吧，不影响问题的推导思路。 ::: 结合公式(5.1.3)，计算得到塑性区修正半径

对比公式（5.1.3）可知，修正后塑性区半径在0角度半径扩大了一倍。

小范围屈服等效模型

欧文（Irwin)认为，如果裂尖塑性区尺寸r远小于裂纹尺寸a，即，此时称为小范围屈服，此时只需要将弹性解加以修正即可，提出等效模型概念。 :::info 裂尖应力超过屈服强度后，裂尖附近产生应力松弛，可以有两种形式，一种是塑性区变形，也就是带来塑性区扩大；一种是裂尖扩展。欧文认为两者等效。 :::
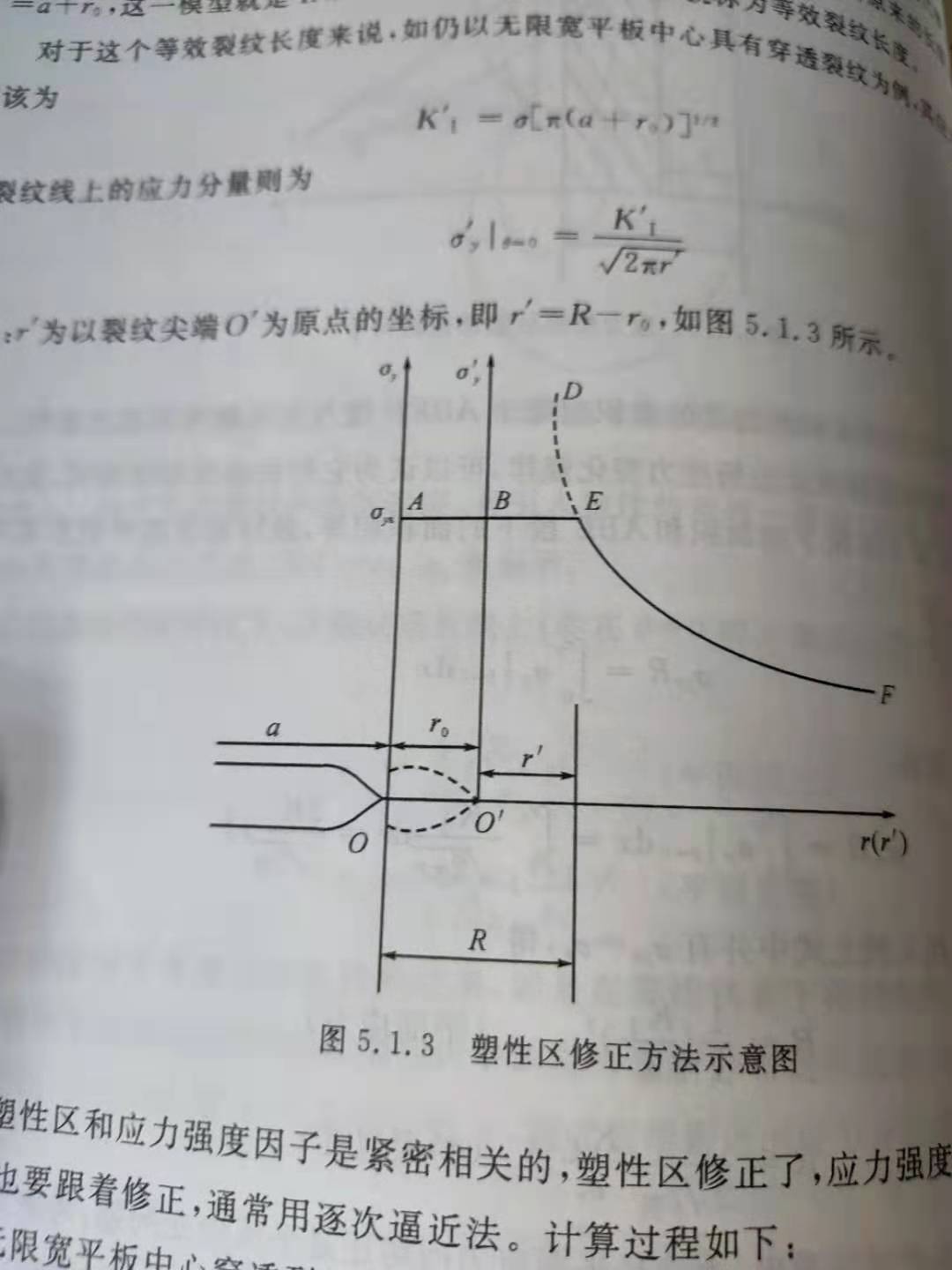
假定将实际的弹塑性应力场用一个假想的弹性应力场替代，也就是将弹塑性的应力松弛用裂尖的扩展替代，裂尖扩展到位置，如图所示。

改变后，也发生改变，即为一个耦合问题，然后迭代法求数值解。

裂纹尖端张开位移（CTOD)

序

这小节理论性不是很强，不是像弹性力学那样完全的基于数学的推导，而是结合了很多的物理概念和假设，需要结合物理思维来理解本小结。

CTOD概念及断裂准则

1965年Wells（威尔斯）在大量实验的基础上，提出了CTOD的概念，裂尖存在的塑性区导致裂纹尖端表面产生了张开，这个张开量就是CTOD，通常用表示。Wells认为，达到极限值就扩展。
解决三方面问题

1. 如何计算，也就是和裂纹几何形状和受载条件的关系。
2. 实验测定临界值。
3. 工程应用

   Irwin小范围屈服下的CTOD

   Irwin假设将裂尖移动到位置，那么原裂纹尖端就产生了张开位移，如下图所示。
   
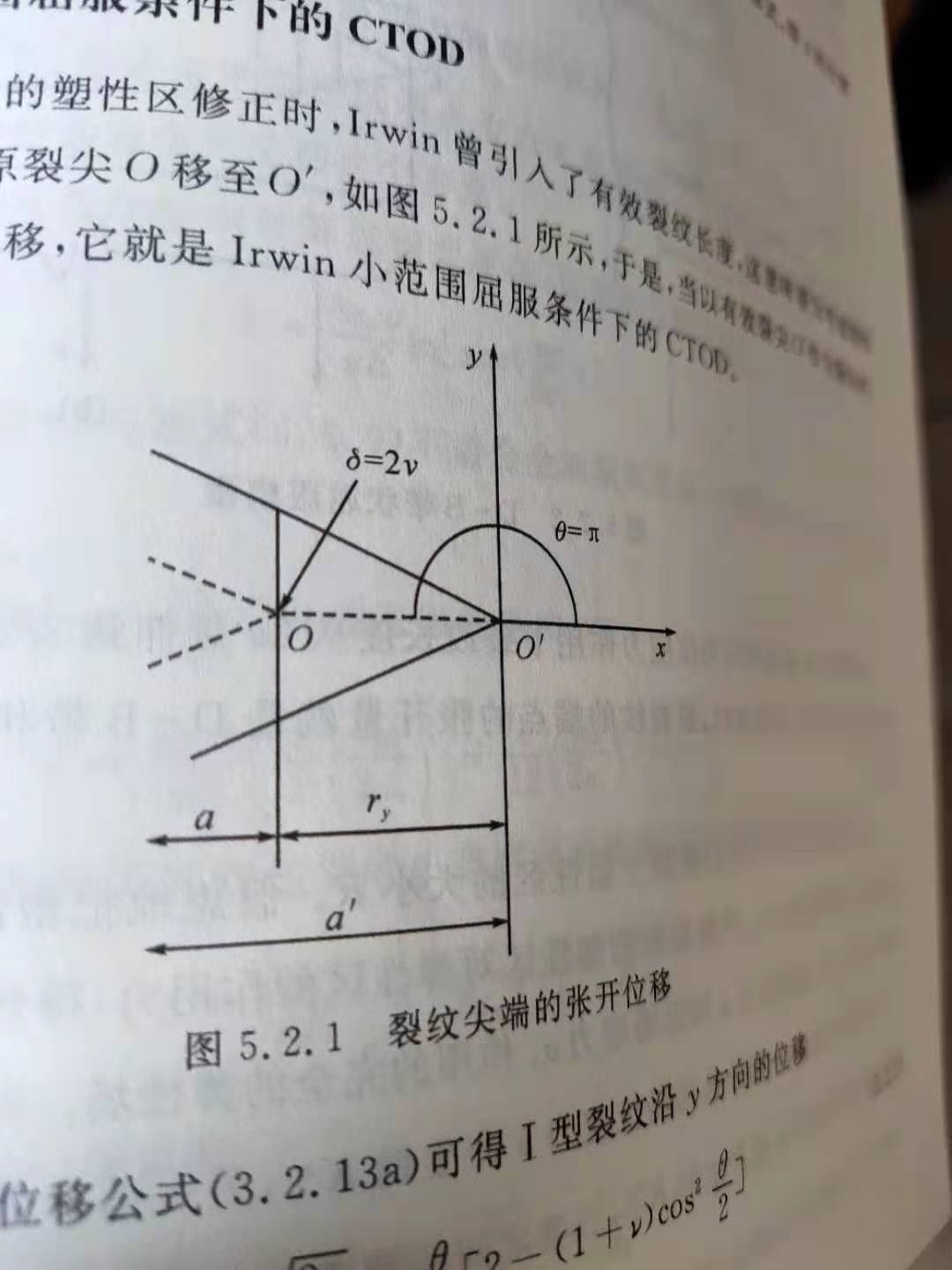
   按照第三章平面的解析，根据位移计算公式就可以得到
   

   D-B带状塑性区模型的CTOD重要

   
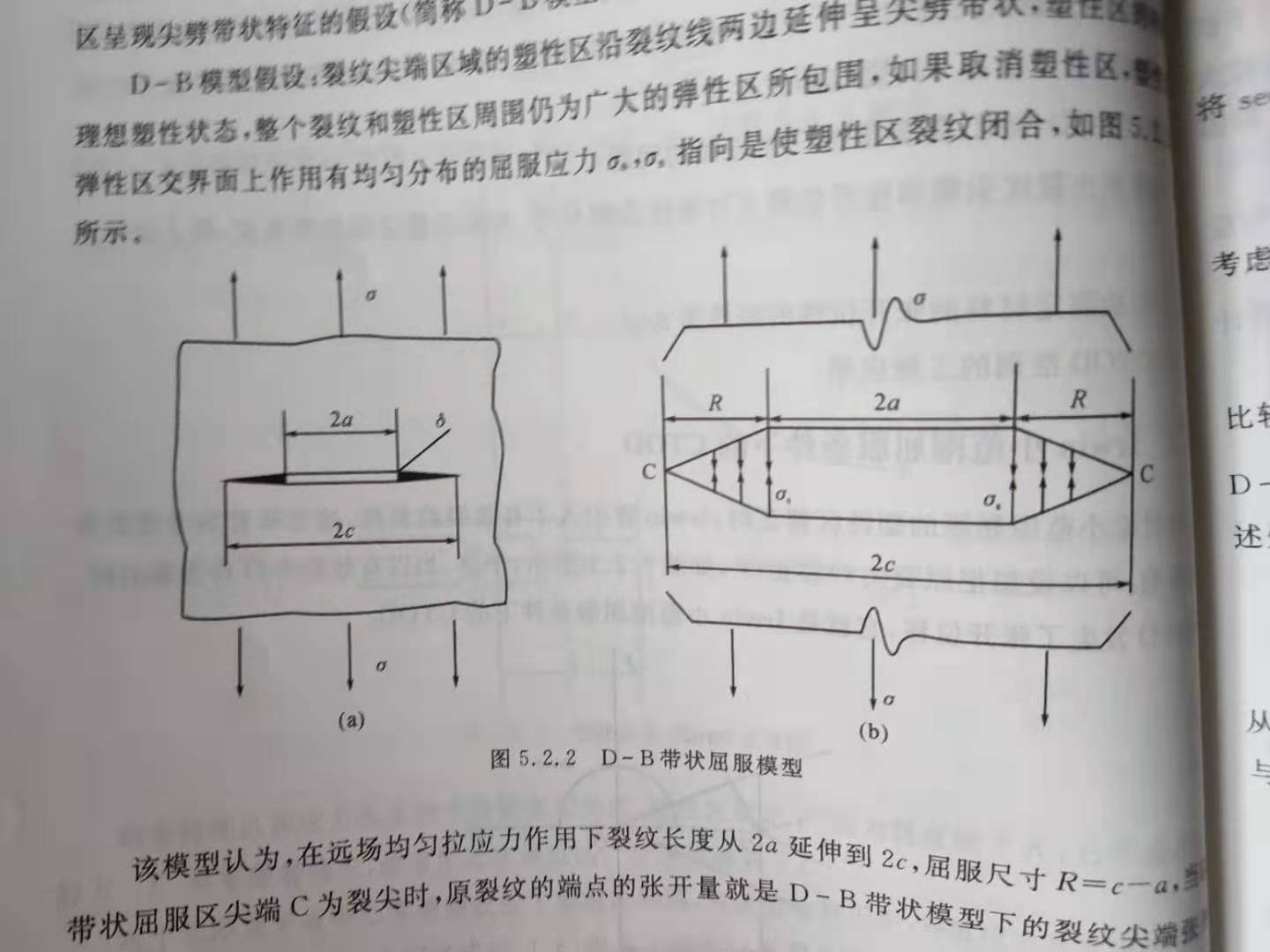
   Dugdale和Barenblatt分别研究中心裂纹薄板拉伸实验，提出裂纹尖端塑性区呈现尖劈带状特征（简称D-B模型）。白色的是裂纹，黑色是塑性区，理想塑性，黑色范围内全部作用屈服应力，使得裂尖张开。
   首先确定塑性区范围R。
   将塑性区挖掉，以作用力替代，按照弹性来求解，叠加原理，一个外面的均布拉力，一个边界力。将C点作为假想的裂尖。
   有意思的分析！由于C点是假想的裂尖，所以应力不存在奇异性，那么

塑性区尺寸

张开位移计算，十分复杂，书上没给出计算过程，只给出结果。

小结

还是化归的思想，转化为熟悉的问题，本来裂尖的塑性区是鱼尾状的，但是这里简化为劈裂状，就是为了符合弹性分析中的裂纹形状。

J积分理论

J积分理论严谨，并且可以实验测量。
两种定义

回路为任一回路C，W为应变能密度，T为应力。

1. 外加荷载通过施加点位移对试样所作出的形变功率。