最原始的复数定义

从虚部单位 i 的定义而言，定义 ，然后就有了虚数的定义。
虚数定义为

引入几何关系后的复数定义

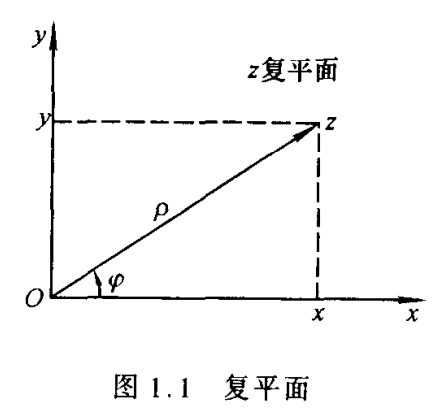
复数是一个二维的向量，两种表示方法，一个是直角坐标，即，一个是极坐标表示法 表示，也就是
(1.1)
其中 称为模值，记作， 称为幅角，记作 ，公式 1.1 称为三角表示法
借助欧拉公式，可以得到:
（1.2） 称为指数表示法

复数的代数运算

加减法 ：
乘法：
除法： :::info 乘除法用指数表达法更加简便 ::: 复数的整数次幂：

整数次根式：

由此可见，如果 是z的幅角的某一值，则 可以取 n 个不同的值。

:::tips 这里用到了复平面的复数的几何含义，转一圈还是同一个复数 :::

无限远点 重要

复平面上模为无穷大的点规定为一点，称为无穷远点。复平面上只有一个无穷远点。