引言

根据复数的复平面的表示方法，复数的幅角增加 后，其值不变，但是复变函数的值可能改变，也就造成了复变函数的多值问题，但是这种多值问题可以通过一定的转换技巧，变成单值函数，因为这种多值问题是一种特殊的自变量多值现象，如果是完全没有规律的多值函数，那么就不好处理了。 :::info 转换的方法就是定义域的变换 :::

多值复变函数及其支点

对于复平面而言 和是同一个点，也就是是同一个复数。
找个多值函数举例说明，，如果规定 ，那么可以得到 ，还有一个函数值 ，这两个函数值，当 时，取值相同，时取值不同，所以把 的点叫做函数的支点。对于这个函数而言，如果复数再转一圈，也就是 ，那么函数值就和 的函数值相等了，这样的支点叫做一阶支点，如果是转两圈，第三圈才又相等，那就叫做二阶支点。

黎曼面 重点难点

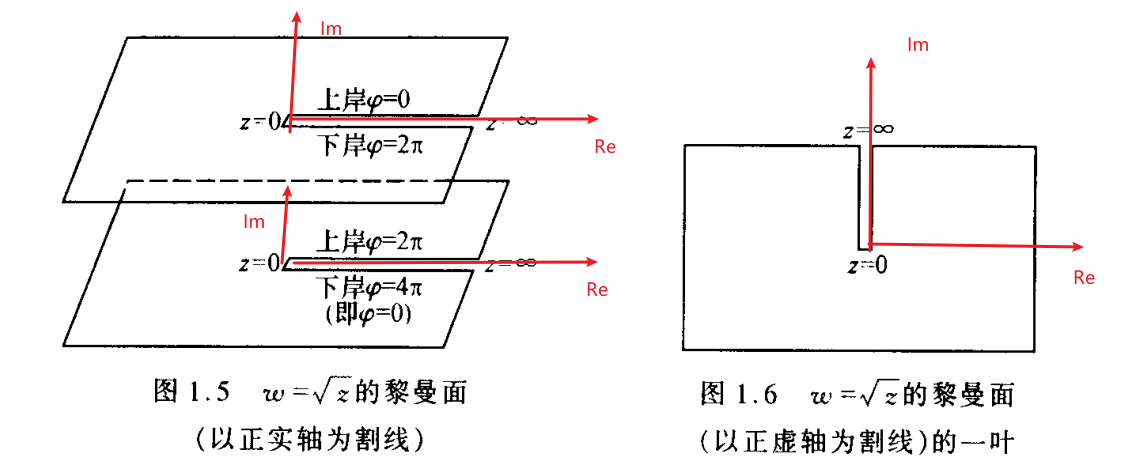
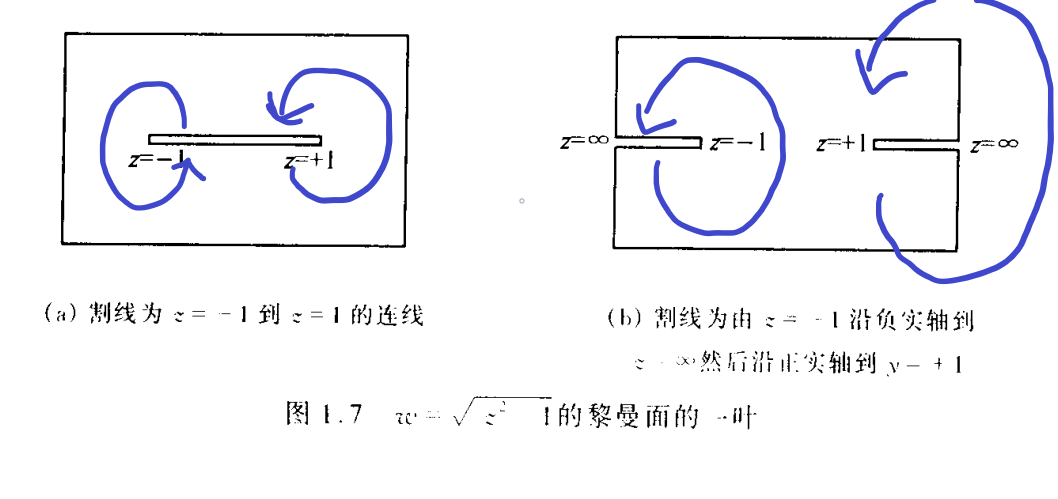
我们讨论当 的情况下，的函数多值问题，其函数值在 和的定义域内是单值的，那么我们就把定义域分解成这两部分，也就是把的复平面剪开，如图1.5所示，然后把上图的下岸和下图的上岸粘接起来，下图的下岸与上图的上岸粘接起来，这种处理后的定义域复平面叫做黎曼面。**隔开的线叫做割线，当然，也可以沿着虚轴剪开，如图1.6所示。每个组成的单叶叫做子叶。 :::info n阶的支点有 n-1 的黎曼面由 n-1 个子叶**组成 ::: 比如函数 ，有两个一阶支点，黎曼面的形式为下图。（按照箭头的方向旋转并且粘接）

几点讨论

• 如果支点的阶数是有限的（自然数），那么称为代数支点，如果是无限的，称为超越支点
• 多值函数是其黎曼面上的单值解析函数
• 最后应当指出，在支点的邻域内无法把各单值分支分开（因为支点对各分支来说是共同的），这点的导数就无法定义，所以多值函数的支点必是奇点