复变函数积分

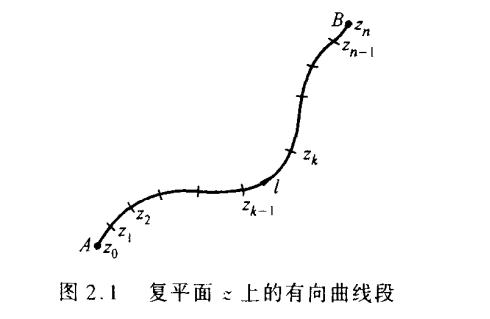
设 是复平面上的一条有向曲线段，起点是A,终点是B.在上给定个复变函数。将分为n个小段，分点依次为(见图2.1)。在每小段上取一点，作和式：
(2.1)
如果，公式 2.1的极限存在且相等，就称此极限为函数在上的积分，记为：

根据复变函数的代数表达法，可以得到：

至此，复变函数的积分问题就转化为两个实变函数的曲线积分问题。

复变函数的积分的性质

1. 如果曲线 可以分为好几段曲线，曲线的走向与曲线 相同，则：
   1. 
2. 若曲线为同一段曲线但是方向相反，积分相反
3. 若为两个 任意复常数，则：
   1.