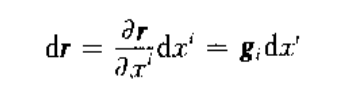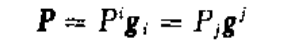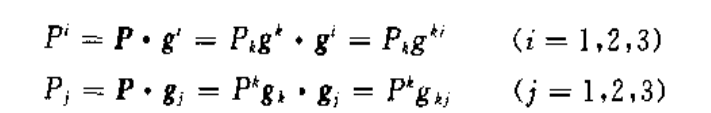二维斜角直线坐标系下的矢量分解

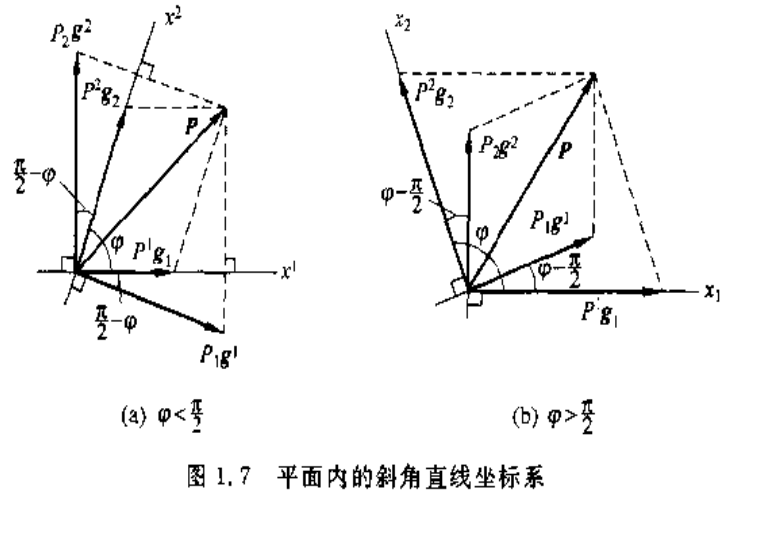
图1.7示出平面内直线坐标系坐标线互不正交。都称为参考矢量，可以不是单位矢量
注意黑体表示矢量

在图1.7中 ，，与笛卡儿坐标系不同，矢量在参考矢量上的投影不等于其分量，而是具有如下关系：
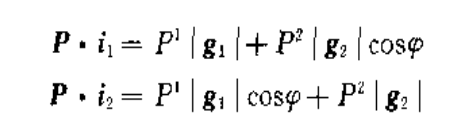（2）

公式（2）是一个二元一次方程组，可以求解矢量的坐标值。这么求太麻烦了，引入逆变参考矢量后，分解的坐标值很好求。

逆变参考矢量与协变参考矢量的关系

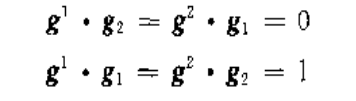
这样求得的逆变参考矢量存在且唯一。
两组参考矢量间存在关系（以及克朗内克符号的引入）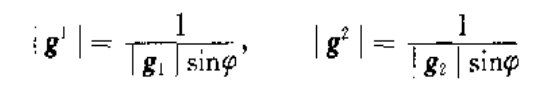
(3)
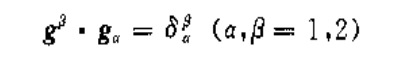（4）

分量的简单求法

用逆变参考矢量表示矢量分解的坐标值很简单，如公式（4）
(5)

公式(2)求解后，带入(3)就得到了(5)，具体的相等的计算过程， 详见下面的[协变基.pdf]，用Mathematica计算的结果。重要

相等的求解过程.pdf

三维斜角直线坐标

三维斜角直线坐标系的建立

用坐标值表示一个点，三个斜角的面是坐标面，三个只有对应坐标值变化的线是坐标线，比如不变，变化，那就是坐标轴

矢经

在建立坐标系后，就可以表示矢经

表示沿三个坐标轴的参考矢量，在直线坐标系中，的大小方向不随空间位置变化而改变（意思就是曲线坐标系会变化）

协变基矢量

矢经对坐标求微分

其中，将矢经对坐标的偏导数定义为协变基矢量

逆变基矢量

一样，满足对偶条件（公式4）就行，满足对偶条件的逆变基矢量存在且唯一，具体的求法有两种，在这里不叙述了，给出协变基和逆变基的几组关系。

同样的，有：

并且有：


我们称 分别为度量张量的协变分量和逆变分量

指标升降关系

自己的思考重要

1. 那么为啥不是一个标量呢，这不是两个矢量的点积吗？不是，这里是并矢的概念，不是点积，是9个标量的统一起来的一个量重要
   1. 计算具体的表示为，这样也和克朗内克符号 对应了起来
   2. 其实这就是度量张量，我们所熟悉的克朗内克符号在三维笛卡尔坐标系下，才是一般理解的单位矩阵，在一般曲线坐标系（例如球坐标系）中，不是单位矩阵。重要难点
2. 这一小结从二维的斜角直线坐标做引入，说明了引入逆变协变这样一对对偶矢量的必要性，然后给出了三维的情况，也就是建立了一组对偶的坐标系，谁是协变，谁是逆变不是很重要，互相的换算关系更为重要。

曲线坐标系重要

三维坐标系的概念重要难点

坐标系也就是坐标的系统，就是如何表示三维一点的坐标。坐标的表示方法确定了，也就是坐标系确定了。

三维空间之所谓是三维，是因为可以用三个独立的坐标表示空间中的任意一点，但是没有规定必须要用什么样的坐标表示，最简单的就是三维正交直线坐标系，也就是笛卡尔坐标系，用三个坐标表示空间中任意一点，但是也可以采用其他的表示方式，比如球坐标，只要是能把空间的全部点全部表示出来的坐标表示法，都可以称为三维空间的点坐标，也就是坐标系。

一般的曲线坐标系及基矢量（一定要区分坐标系和基矢量的概念）

对于笛卡尔坐标系而言，坐标轴就是三条正交的直线，基矢量一但选取，不随点空间位置的改变而改变，大小方向都不变。但是对于一般的曲线坐标而言，坐标系是确定的（也就是如何表示点的方法），但是基矢量随着点的位置变化，大小或者方向都可能改变。重要难点

用三维球坐标系来举例说明曲线坐标系的基矢量的选取方法。

同样借助矢经的概念，从原点出现的矢经，其微分可以表示为：

也可以表示为一般的形式

那么，可以这样选取基矢量

这样一来，之前所讲的所有关系协变和逆变的关系，全部可以用到曲线坐标系，但是要注意，这里的的大小方向随点位置的变化而变化，所以可以叫做局部基矢量。并且，不是只有这么一种选取基矢量的方法，这样的基矢量也叫做自然局部基矢量。

总结

至此，将坐标系及协变量、逆变量的概念介绍完毕。下面以一个图表示从头一步一步的进展关系。

**