（01）钱的时间价值、有效年利率

• 分享一些正确的投资理财观念，感兴趣可关注我的知识库：

陈瑞娇

1、Time value of money（钱的时间价值）、折现率

• 今天的一块钱，不等于明天的一块钱。
• 不同时间点上的钱不能直接比较，应折现到同一时间点上才能直接比较（依靠折现率进行折现）。
• 假设年利率为 10%：
  • 100 块钱存银行，则一年后将得到 110。
    • 
  • 即：一年后的 110 相当于现在的 100（此时折现时的折现率即为 10%）
    • 
• 假如你有 ￥100 可投资于两个项目中的一个（假设折现率为 10%）：
  • 项目 1：第一年产生 ￥70、第二年产生 ￥50、第三年产生 ￥20=121.3
  • 项目 2：第一年产生 ￥20、第二年产生 ￥30、第三年产生 ￥100=118.1
• 你会选择投资哪一个项目？
  • 项目 1 的现金流折现到当前：

• 项目 1 的现金流折现到当前：

• 因此，应该选择项目 1 进行投资（尽管项目 1 三年的现金流总和小于项目 2 的，但折现到当前却比项目 2 要高）

• 相关概念：
  • Discount rate（折现率）：the interest rate we use to discount payements to be made in the future, usually used interchangeably with the interest rate.（折现率的定义）
  • Required rate of return（要求回报率）：the return that investors and savers require to get them to willingly lend their funds
• 任何一个产品的要求回报率都等于一个无风险利率加上相应的风险溢价（只要承担风险，就需要得到风险补偿）
• 一般可将靠谱国家的国债利率当做无风险利率，如美国国债对应的利率即为无风险利率（risk-free rate）

• Required interest rate on a security = nominal risk-free rate + default risk（违约风险）premium+ liquidity（流动性）risk premium + maturity（期限）risk premium

  - 违约：不还钱、还款不足、不按时还，均属于违约
  - 流动性：交易活跃程度
  - 时间越长，maturity risk 越大，相应的 premium 越高
  - 风险溢价并不是只包含以上三种，只是以上三种最为常见

  2、有效年利率（EAR，Effective Annual Rate）

• 单利：只有本金参与计息，利息不再参与计息（一年按 360 天计算）

• 复利：本金和利息均参与计息（一年按 365 天计算）
  • 后续均为复利，除非特别指出

• Effective Annual Rate（有效年利率）：投资 n 年，按利滚利的形式计算一年实实在在的年化收益率（一年可能计息多次）

  • 示例：1 块钱，投资一年，假设年利率为 10%：
    • 一年计息 1 次：
    • 一年计息 2 次：
      • 即半年计息一次，半年利息为
    • 一年计息 4 次：
    • 一年计息 365 次：
    • 一年计息 m 次：
    • 注意：
      • 是一年计息 m 次，得到的才是有效年利率（不是 n 年计息 m 次）
      • 如果要求计算 m，则采用试错法求解
      • 当 m 趋向于无穷大时，求极限可得
        • 为年利率，当时，
      • 特点：m 越大（一年计息次数越多），EAR 越大

        3、Annuities（年金）

• 符合以下特征的有限时间序列现金流（a finite set of level sequential cash flows）即为年金：

  • 等时间间隔
  • 等现金流
  • 相同方向
• 年金示例：
  • 等额还房贷
  • 等额还租金
• 金融计算器计算年金（注意，需掌握基本金融计算器的使用）：
  • N：Number of periods（一共多少期，注意是期数，不是年数）
  • I/Y：interest rate per period（期间利率，即每一期的利率，如果利率为 x%，则 I/Y 的值即为 x）
  • PMT：amount of each periodic payment（每一期的同向现金流）
  • PV：Present Value
  • FV：Future Value

• 相关概念：

  • FV（Future value）：amount to which investment grows after one or more compounding periods
  • PV（Present value）：Current value of some future cash flow
  • CF：Cash Flow（现金流）

    （1）ordinary annuities（后付年金）：期末产生 CF

• 如 3 年，每年年末得 100，则：

  • 
    • 可通过金融计算器计算，计算时 FV 设置为 0，即可求 PV
  • 
    • 可通过金融计算器计算，计算时 PV 设置为 0，即可求 FV

      （2）annuity due（先付年金）：期初产生 CF

• the first cash flow occurs immediately，at t=0

• 案例：租金（rental fees）、学费（tuition fees）、生活费（living expenses）

• 如 3 年，每年年初得 100，则：

  • 
    • 可通过金融计算器计算，计算时 FV 设置为 0，即可求 PV
  • 
    • 可通过金融计算器计算，计算时 PV 设置为 0，即可求 FV
  • 如果使用计算器计算，需要先调整计算器为先付年金模式 BGN（默认为后付年金模式，END）
    • 按 2ND + PMT 可查看当前模式（默认为 END）
    • 按 2ND + ENTER（即 SET）可切换模式
  • 先付年金的 FV 和 PV 均比相应的后付年金的大 (1+ I/Y) 倍
    • 先付年金的 PV 等同于后付年金的 PV * (1+ I/Y)
    • 先付年金的 FV 等同于后付年金的 FV * (1+ I/Y)
    • 基于该特性，如果要求先付年金，可以求对应的后付年金，随后再推导出先付年金

      （3）perpetuity（永续年金）

• perpetuity（永续年金）：a financial instruments that pays a fixed amount of money at set intervals over an infinite period of time.

  • 特殊的后付年金：现金流发生在每一期期末，且永续无限
  • 时间永续，因此没办法求 FV，只能求 PV

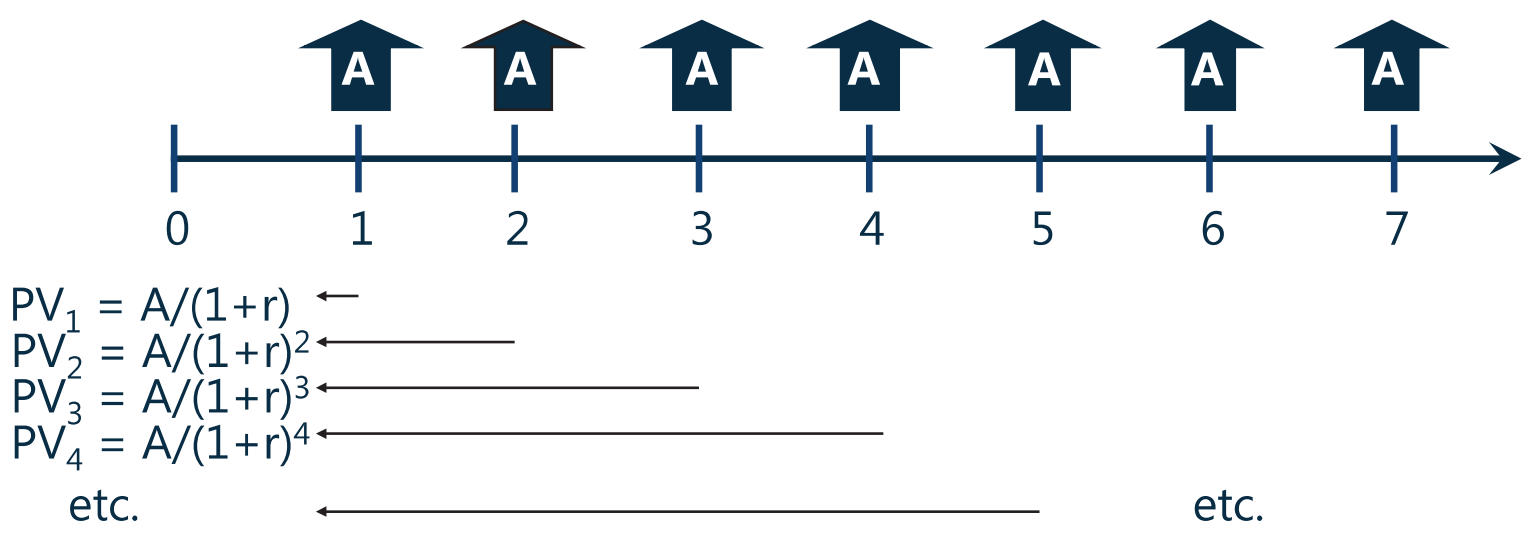
• 推导公式
  • 
  • 两边同乘以 得：
  • 
  • 两式相减，且忽略等号右边最后一项（接近无穷小），可得：
  • 
  • 因此：
    • 

• 应用：优先股、永续债

  • 对优先股求定价时，都是用永续年金的求 PV 的方法
    • 因为优先股是给股东每期等额的红利，且假设公司是连续经营下去的
  • 永续债

    4、基于现金流计算年化利率

• 任何一个东西都有成本（天上即使真的掉馅饼，捡饼也同样有机会成本），资金也不例外，资金的成本即利率（利息）。比较利率高低时，通常都折算为统一的利率单位 —— 年利率。

  • 马云路上掉了 ￥100，他也不会去捡回，因为捡回 ￥100 所花的几秒时间里，他干其它事情都能赚 ￥10000 了，该场景下马云捡回 ￥100 元的机会成本就是 ￥10000。
• 将不同时间点上的现金流按指定利率折现到当前时间点，即可获得不同时间点上的现金流在当前时间点的实际价值。
• 因此，如果已知期初投入和后续每年产生的现金流，即可通过以下公式计算得到值（即年化回报率、年化利率）：

• 以上求解公式其实可以使用金融计算器快速求解。后续在该文中会继续推出关于银行各种贷款（如消费贷、信用贷）的年化利率的计算方式（原理同以上公式，会使用金融计算器进行计算）。