MySQL 索引 索引机制 索引原理
推荐文章:
索引的定义
索引是为了加速对表中数据行的检索而创建的一种分散存储的数据结构。
MySQL 的索引是硬盘级,索引数据是保存在硬盘上的,有部分数据可以放入缓存,后面的文章会描述到, InnerDB 有一个缓存池,缓存池的大小是可以通过配置文件配置。
我们通过下图来看看 MySQL 的索引是怎么工作的?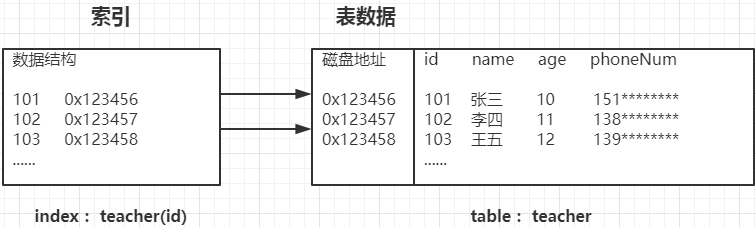
比如我们建了一张老师表,有 N 条数据,每条数据对应有一个磁盘地址,在没有引入索引机制的情况下,我们要查一条姓名等于王五的数据,我们需要一条一条比对老师表的所有数据,当老师表的数据量比较多时,全表比对检索的速度会非常慢。
这样我们就必须引入索引机制,比如我们对 id 建了一个索引,要查一条 id 等于101的数据,我们可以通过索引的数据结构快速检索出 id 等于101的磁盘地址,这样就可以通过磁盘地址快速定位到表中的数据。
索引的好处
索引能极大的减少存储引擎需要扫描的数据量。
索引可以把随机 IO 变成顺序 IO。
索引可以帮助我们在进行分组、排序等操作时,避免使用临时表。
索引的数据结构
MySQL 为什么要选用 B+Tree 的数据结构来作为它的索引机制?接下里我们一步一步来推敲。
国外的数据结构模拟网站:https://www.cs.usfca.edu/~galles/visualization/Algorithms.html,可以通过该网站模拟各种数据结构的创建过程。
二分查找
二分查找法(binary search)也称为折半查找法,用来查找一组有序的记录数组中的某一记录。
基本思想是:将记录按有序化(递增或递减)排列,在查找过程中采用跳跃式方式查找,即先以有序数列的中点位置作为比较对象,如果要找的元素值小于该中点元素,则将待查序列缩小为左半部分,否则为右半部分。
通过一次比较,将查找区间缩小一半,O(logN) 的时间复杂度。
# 给出一个例子,注意该例子已经是升序排序的,且查找数字 48数据:5, 10, 19, 21, 31, 37, 42, 48, 50, 52下标:0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- 步骤一:设 low 为下标最小值0,high 为下标最大值9。
- 步骤二:通过 low 和 high 得到 mid,mid=(low + high) / 2,初始时 mid 为下标4,也可以是5,看具体算法实现。
- 步骤三:mid = 4对应的数据值是31,31 < 48(我们要找的数字)。
- 步骤四:通过二分查找的思路,将 low 设置为31对应的下标4,high 保持不变为9,此时 mid 为6。
- 步骤五:mid = 6对应的数据值是42,42 < 48(我们要找的数字)。
- 步骤六:通过二分查找的思路,将 low 设置为42对应的下标6,high 保持不变为9,此时 mid 为7。
- 步骤七:mid = 7对应的数据值是48,48 == 48(我们要找的数字),查找结束。
通过3次二分查找就找到了我们所要的数字,而顺序查找需8次。
二叉查找树(Binary Search Tree)
首先,要提高数据检索的效率,我们第一个考虑的数据结构就是二叉查找树。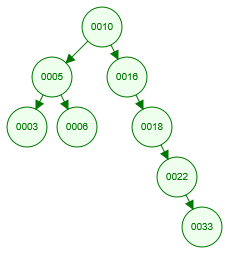
二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
假设该二叉查找树保存的是 id 索引,我们要检索一条 id=8 的数据,它会一个节点一个节点比对,首先把根节点(第一条插入的数据就是根节点)加载到内存中比对,8比10要小,这个时候会找10左边的节点,再把5加载到内存中比对,5比8要小,继续找5右边的节点,最后找到8这个节点。
二叉查找树的问题
比如我们生成一个如下图所示的二叉树: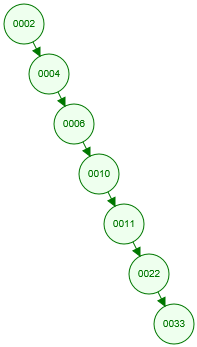
我们每次在插入新的节点的时候,数据都比上一个插入的节点大,这样就形成了如上图所示的链表的关系,当我们要去检索一条 id 等于33的时候,它检索的效率和全表扫描一样了,没有任何优化。
所以二叉查找树检索的效率取决于二叉查找树数据的分布,当二叉查找树数据的分布相当于一个线性链表的时候,它的数据检索效率将会非常低。
平衡二叉查找树(Balanced Binary Tree)
平衡二叉搜索树(英语:Balanced Binary Tree)是一种结构平衡的二叉搜索树,即叶节点高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。它能在 O(log n) 内完成插入、查找和删除操作,最早被发明的平衡二叉搜索树为 AVL 树。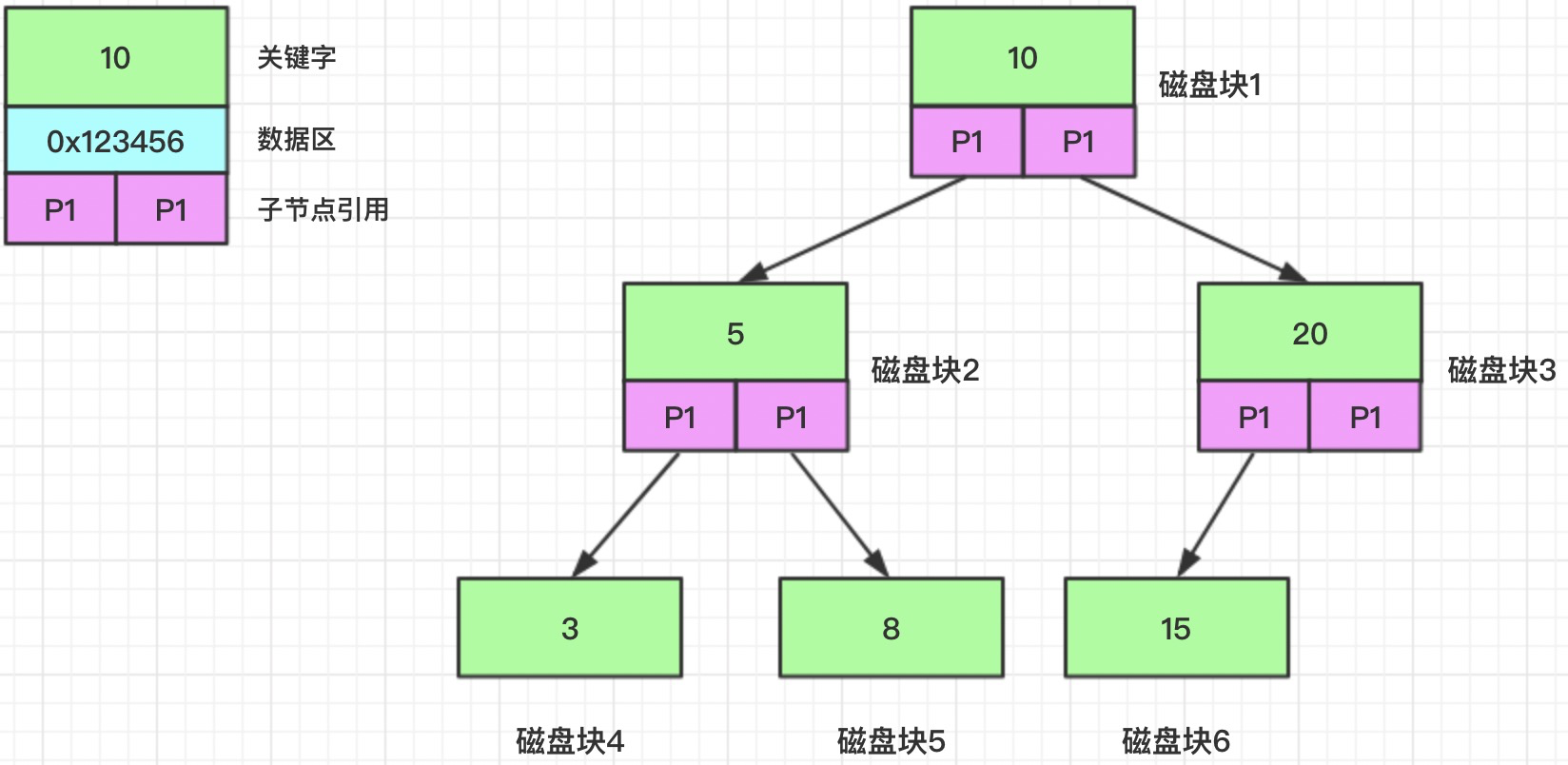
注意:上图省略了数据区
当平衡二叉查找树发生节点变更时,基于每个节点的平衡因子,通过一次或多次左旋和右旋来达到树新的平衡。
磁盘块是一个节点在硬盘中的保存位置,每个节点有三块数据内容:关键字、数据区、子节点引用。
- 关键字:比如我们用 ID 作为索引,那这里保存的就是 ID 内容。
- 数据区:可以是数据的磁盘位置,可以是真正的数据内容。
- 子节点引用:比如跟节点10的 P1 引用指向的是5节点,P2 引用指向的是20节点,基于 P1 和 P2 就可以通过顺序 IO 的方式加载子节点磁盘块的内容到内存中。
平衡二叉查找树的问题
太深了
数据处的深度决定着它的 IO 操作次数,IO 操作耗时大。比如要加载 ID 等于8的数据,需要3次 IO 操作,6条数据就就需要3次 IO 操作,当我们的数据量达到千万级别的时候,这颗平衡二叉查找树会很高,数据检索时的 IO 操作次数会更多。
太小了
每一个磁盘块(节点/页)保存的数据量太小了,没有很好的利用操作磁盘 IO 的数据交换特性,也没有利用好磁盘 IO 的预读能力(空间局部性原理),从而带来平凡的 IO 操作:
- 磁盘 IO 的数据交换特性:一次 IO 操作,交换的数据是 4K(一页)。
- 磁盘 IO 的预读能力:操作系统在做 IO 操作的时候,一次不止加载 4K 的数据量,它会利用空间局部性原理,加载更多的数据,MySQL 的一页数据是 16K。
多路平衡查找树(B-Tree)
m 阶 B-Tree 满足以下条件:
- 每个节点最多拥有 m 个子树。
- 根节点至少有2个子树。
- 分支节点至少拥有 m/2 颗子树(除根节点和叶子节点外都是分支节点)。
- 所有叶子节点都在同一层、每个节点最多可以有 m-1 个 key,并且以升序排列。
下图是一个2-3 B树的结构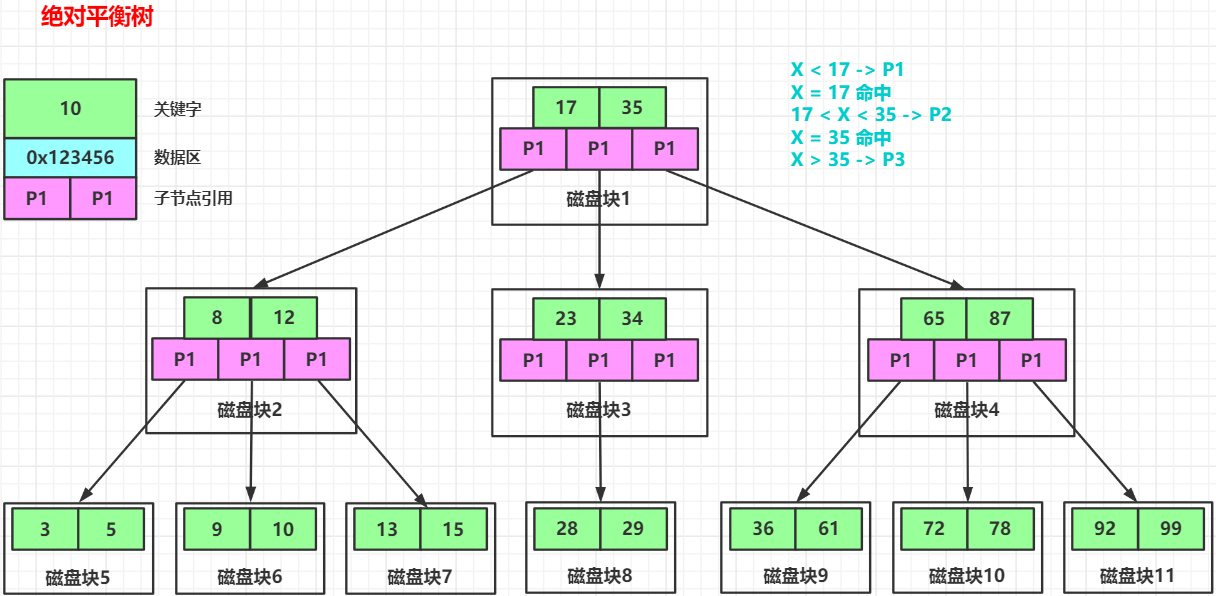
注意:上图省略了数据区
对比平衡二叉查找树,同样最多三次 IO 操作,2-3 B树最多可以检索到的数据量是22条数据,而平衡二叉查找树最多可以检索到的数据量是8条,当多路平衡二叉查找树的路数越多,在 IO 操作次数相同的情况下,它能检索的数据量越多。
为什么要合理的设置 MySQL 的字段长度?
比如我们用 MySQL 页的定义,一次 IO 操作会加载 16k 的数据,用 int 类型的 id 做索引,int 类型的数据暂用的空间大小是 4bit,假设再冗余 4bit 作为引用、数据区的大小,这样 MySQL 的一页数据能存放 16*1024/8=2048 个关键字。
所以我们在定义 MySQL 字段类型的时候,尽量要精简一些,字段的长度要设定的比较合理,能短则短,否则如果我们把这个字段作为索引,它会影响 B-Tree 的路数,进而影响索引的检索效率。
为什么 MySQL 的索引不宜建多?
多路平衡二叉查找树为了保证树的绝对平衡,会在树中节点变更的时候,采用分裂、合并的操作来维持树的绝对平衡。
所以我们不能建过多的索引,会拖慢 MySQL 的新增、更新、删除操作,因为每次数据变更,都会对所有的索引数据进行节点的变更。
加强版多路平衡查找树(B+Tree)
B+Tree 是在 B-Tree 基础上的一种优化,使其更适合实现外存储索引结构,InnoDB 存储引擎就是用 B+Tree 实现其索引结构。
从 B-Tree 结构图中可以看到每个节点中不仅包含数据的 key 值,还有 data 值。而每一个页的存储空间是有限的,如果 data 数据较大时将会导致每个节点(即一个页)能存储的 key 的数量很小,当存储的数据量很大时同样会导致B-Tree 的深度较大,增大查询时的磁盘 I/O 次数,进而影响查询效率。在 B+Tree 中,所有数据记录节点都是按照键值大小顺序存放在同一层的叶子节点上,而非叶子节点上只存储 key 值信息,这样可以大大加大每个节点存储的 key 值数量,降低 B+Tree 的高度。
B+Tree 相对于 B-Tree 有几点不同:
- B+Tree 节点关键字搜索采用左闭合区间。
- B+Tree 非叶节点不保存数据相关信息,只保存关键字和子节点的引用。
- B+Tree 关键字对应的数据保存在叶子节点中。
B+Tree 叶子节点是按照数据的升序排列的,并且相邻节点具有顺序引用的关系。
- 叶子节点中的数据在物理存储上是无序的,仅仅是在逻辑上有序(通过指针串在一起,可以是双向链表)。
下面是一个 B+Tree 的数据结构图: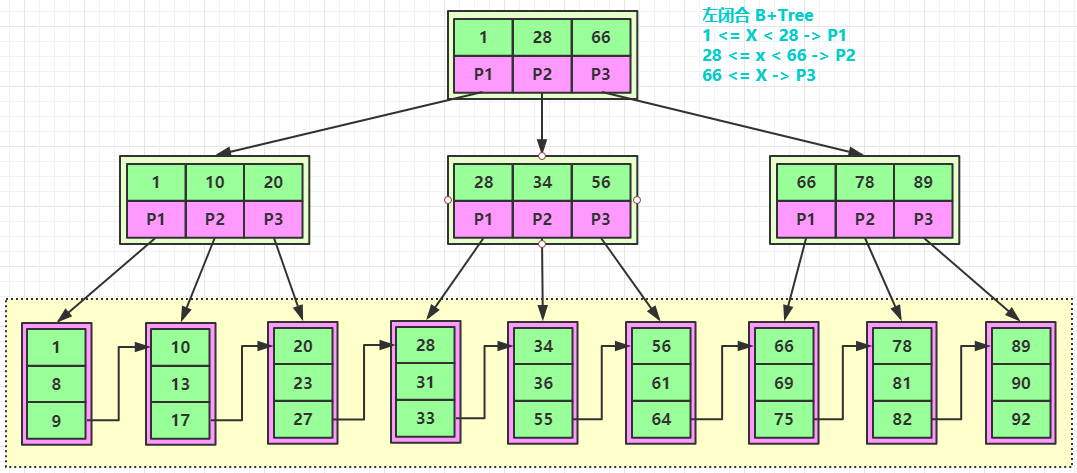
注意:上图的结构不是经典的 B+Tree 结构。
为什么选用 B+Tree?
B+Tree 是 B-Tree 的变种(PLUS版)多路绝对平衡查找树,它拥有 B-Tree 的优势。
B+Tree 扫库、表能力更强。
如果要从 B-Tree 中扫描表数据的话,基本要把整棵树都要扫描一遍,因为每个节点都存在数据区。B+Tree 就不需要扫描整棵树,只需要扫描叶子节点就可以了。
- B+Tree 的磁盘读写能力更强。
B+Tree 的节点上是不保存数据的,那么它保存的关键字就更多,这样一次 IO 操作,加载的关键字就更多,所以它的磁盘读写能力更强。
- B+Tree 的排序能力更强。
B+Tree 的叶子节点天然就是顺序存放的。
- B+Tree 的查询效率更加稳定。
比如我们从上图的 B-Tree 中查询一条 id 等于8的数据需要经过两次 IO 操作,查询一条 id 等于3的数据需要经过三次 IO 操作,而从上图的 B+Tree 中只有叶子节点才保存数据,所以查询任何数据都需要经过三次 IO 操作。 所以 B+Tree 的查询效率更加稳定。
B+Tree
补充一些 B+Tree 的知识点。
B+Tree 的特性
- 在块设备上,通过 B+Tree 可以有效的存储数据。
- 所有记录都存储在叶子节点上,非叶子(non-leaf)存储索引(keys)信息。
- B+Tree 含有非常高的扇出(fanout),通常超过100,在查找一个记录时,可以有效的减少 IO 操作。
B+Tree 的操作
B+Tree 的插入
B+Tree 的插入必须保证插入后叶子节点中的记录依然排序。
插入操作步骤(引用自姜老师的书《MySQL 技术内幕:InnoDB 存储引擎(第2版)》第5.3.1小节)
| Leaf Page 满 | Index Page 满 | 操作 |
|---|---|---|
| No | No | 直接将记录插入到叶子节点 |
| Yes | No | 1. 拆分 Leaf Page 1. 将中间的节点放入到 Index Page 中 1. 小于中间节点的记录放左边 1. 大于或等于中间节点的记录放右边 |
| Yes | Yes | 1. 拆分 Leaf Page 1. 小于中间节点的记录放左边 1. 大于或等于中间节点的记录放右边 1. 拆分 Index Page 1. 小于中间节点的记录放左边 1. 大于中间节点的记录放右边 1. 中间节点放入上一层 Index Page |
B+Tree 总是会保持平衡。但是为了保持平衡对于新插入的键值可能需要做大量的拆分页(split)操作;部分情况下可以通过 B+Tree 的旋转来替代拆分页操作,进而达到平衡效果。
MySQL 单页数据不会插满,会有一定的预留空间,比如 16K 的空间只会使用 15K,MySQL 为什么要这么设计呢?
比如说我们要更新表中的某条记录,将本来是200字节的数据,更新成了300字节,如果 MySQL 允许把 16K 的数据空间都占满,一旦表中的数据发生更新,这个时候就不能原地更新,会发生 split 操作。
split 是竞争比较大的操作,split 操作改变了树的结构,在执行的过程中会加一些锁操作,竞争就会比较多,会降低 MySQL 的更新、插入的执行效率。
所以一般设计表结构的时候要考虑在更新数据的时候,减少 MySQL 的 split 操作,尽量让 MySQL 能实现原地更新,可以使用空间换时间的方式。
B+Tree 的删除
B+Tree 使用填充因子(fill factor)来控制树的删除变化,50% 是填充因子可设的最小值。B+Tree 的删除操作同样必须保证删除后叶子节点中的记录依然排序。与插入不同的是,删除根据填充因子的变化来衡量。
删除操作步骤(引用自姜老师的书《MySQL 技术内幕:InnoDB 存储引擎(第2版)》第5.3.2小节)
| 叶子节点小于填充因子 | 中间节点小于填充因子 | 操作 |
|---|---|---|
| No | No | 直接将记录从叶子节点删除,如果该节点还是 Index Page 的节点,用该节点的右节点代替 |
| Yes | No | 合并叶子节点和它的兄弟节点,同时更新 Index Page |
| Yes | Yes | 1. 合并叶子节点和它的兄弟节点 1. 更新 Index Page 1. 合并 Index Page 和他的兄弟节点 |
B+Tree 的旋转
- B+Tree can incorporate rotation to reduce the number of page splits.
- A rotation occurs when a leaf page is full, but one of its sibling is not full.
- Rather than splitting the leaf page, we move a record to its sibling, adjusting the indices as necessary. Typically, the left sibling is checked first (if it exists) and then the right sibling.
B+Tree 的扇出(fan-out)
B+Tree 图例: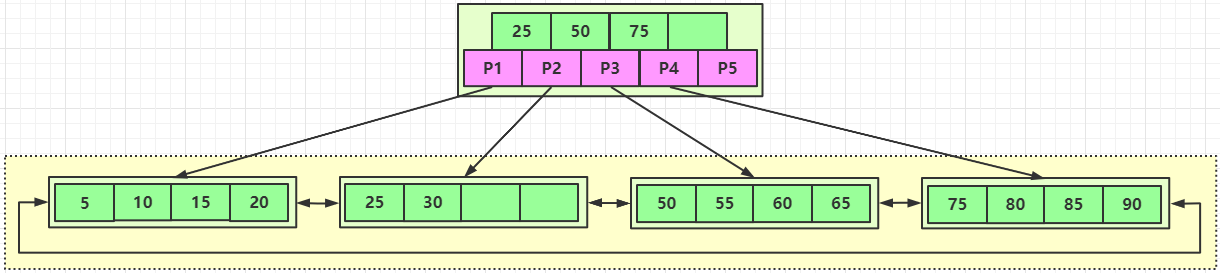
- 该 B+Tree 高度为2
- 每叶子页(LeafPage)4条记录
- 扇出数为5
- 叶子节点(LeafPage)由小到大(有序)串联在一起
扇出是每个索引节点(Non-LeafPage)指向每个叶子节点(LeafPage)的指针。
扇出数 = 索引节点(Non-LeafPage)可存储的最大关键字个数 + 1。
图例中的索引节点(Non-LeafPage)最大可以存放4个关键字,但实际使用了3个。
B+Tree 存储数据举例
假设 B+Tree 中页的大小是 16K,每行记录是 200Byte 大小,求出树的高度为1,2,3,4时,分别可以存储多少条记录。
-- 查看数据表中每行记录的平均大小mysql> show table status like "%employees%"\G*************************** 1. row ***************************Name: employeesEngine: InnoDBVersion: 10Row_format: DynamicRows: 298124Avg_row_length: 51 -- 平均长度为51个字节Data_length: 15245312Max_data_length: 0Index_length: 0Data_free: 0Auto_increment: NULLCreate_time: 2015-12-02 21:32:02Update_time: NULLCheck_time: NULLCollation: utf8mb4_general_ciChecksum: NULLCreate_options:Comment:1 row in set (0.00 sec)
高度为1
- 16K/200B 约等于 80 个记录(数据结构元信息如指针等忽略不计)。
高度为2
非叶子节点中存放的仅仅是一个索引信息,包含了 Key(索引键值) 和 Point 指针;Point 指针在 MySQL 中固定为 6Byte。而 Key 我们这里假设为 8Byte,则单个索引信息即为14个字节,KeySize = 14Byte。
- 高度为2,即有一个索引节点(索引页),和 N 个叶子节点。
- 一个索引节点可以存放 16K / KeySize = 16K / 14B = 1142个索引信息,即有(1142 + 1)个扇出,以及有(1142 + 1)个叶子节点(数据页),可以简化为1000。
- 数据记录数 = (16K / KeySize + 1)x (16K / 200B) 约等于 80W 个记录
高度为3
- 高度为3的 B+Tree,即 ROOT 节点有1000个扇出,每个扇出又有1000个扇出指向叶子节点。每个节点是80个记录,所以一共有 8000W个记录。
高度为4
- 同高度3一样,高度为4时的记录书为(8000 x 1000)W
上述的 8000W 等数据只是一个理论值。线上实际使用单个页的记录数字要乘以 70%,即第二层需要 70% x 70% ,依次类推。
因此在数据库中,B+Tree 的高度一般都在2~4层,这也就是说查找某一键值的行记录时最多只需要2到4次 IO,2~4次的 IO 意味着查询时间只需0.02~0.04秒(假设 IOPS=100,当前 SSD 可以达到 50000IOPS)。
从 5.7 开始,页的预留大小可以设置了,以减少 split 操作的概率(空间换时间)。
IOPS(Input/Output Operations Per Second)是一个用于电脑存储设备(如硬盘(HDD)、固态硬盘(SSD)或存储区域网络(SAN))性能测试的量测方式,可以视为是每秒的读写次数。
作者:殷建卫 链接:https://www.yuque.com/yinjianwei/vyrvkf/ei2evb 来源:殷建卫 - 架构笔记 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。

