WebGl - 08 2D Matrices - 《代码知识结构》

一. 矩阵转化的基本原理
二 . 点在二维空间中点基本运动
三. 再一步转化

【 二维矩阵转化 】每种变换都改变了着色器并且这些变换还受先后顺序影响。在前例中我们先缩放，再旋转，最后平移，如果执行顺序不同结果也不同。

一. 矩阵转化的基本原理

例如这是缩放 2, 1 ，旋转30度，然后平移 100, 0 的结果。

平移 100, 0 ，旋转30度，然后缩放 2, 1 的结果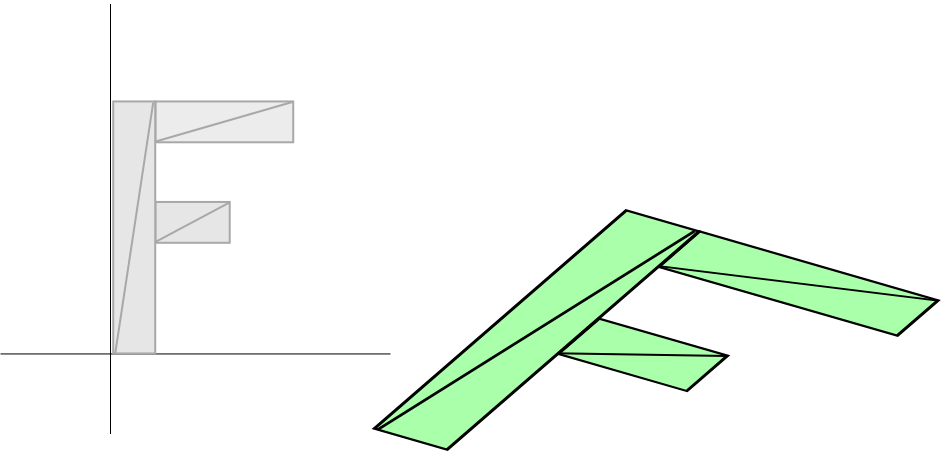

聪明的人可能已经想到了矩阵，对于二维我们使用 3x3 的矩阵， 3x3 的矩阵就像是有9个格子的格网
1.0 2.0 3.0
4.0 5.0 6.0
7.0 8.0 9.0
在计算的时候我们将位置坐标沿着矩阵列的方向依次相乘再将结果加起来。我们的位置信息只有两个值， x 和 y 。但是要进行运算需要三个值，所以我们将第三个值赋值为 1 。
在这个例子中结果将是

newX =	x *	1.0	+	newY =	x *	2.0	+	extra =	x *	3.0	+
	y *	4.0	+		y *	5.0	+		y *	6.0	+
	1 *	7.0			1 *	8.0			1 *	9.0

你可能会想“这样做有什么意义？”，好吧，假设我们要进行平移，平移的量为 tx 和 ty ，然后定义一个这样的矩阵
1.0 0.0 0.0
0.0 1.0 0.0
tx ty 1.0
然后计算结果

newX =	x	*	1.0	+	newY =	x	*	0.0	+	extra =	x	*	0.0	+
	y	*	0.0	+		y	*	1.0	+		y	*	0.0	+
	1	*	tx			1	*	ty			1	*	1.0

如果你还记得线性代数的知识，我们可以删除和 0 相乘的部分，和 1 相乘相当于没变，所以简化后为

newX =	x	*	1.0	+	newY =	x	*	0.0	+	extra =	x	*	0.0	+
	y	*	0.0	+		y	*	1.0	+		y	*	0.0	+
	1	*	tx			1	*	ty			1	*	1.0

或者更简洁
newX = x + tx;
newY = y + ty;

其他的就不用关心了。这个看起来和平移例子中的代码有些相似。
同样的来实现旋转，在旋转章节提到过，旋转只需要和旋转角对应的正弦和余弦值
s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);
然后我们创建一个这样的矩阵

c	-s	0.0
s	c	0.0
0.0	0.0	1.0

使用矩阵后得到

newX =	x	*	c	+	newY =	x	*	-s	+	extra =	x	*	0.0	+
	y	*	s	+		y	*	c	+		y	*	0.0	+
	1	*	0.0			1	*	0.0			1	*	1.0

遮住没有意义的部分（和 0 或 1 相乘的部分）
然后得到简化版
newX = x c + y s;
newY = x -s + y c;

正是我们在旋转例子中得到的结果。
同理我们可以在缩放的例子中的得到
newX = x * sx;
newY = y * sy;
现在你可能还会想“那又怎样，有什么意义？”，好像花了更多精力做之前做过的事情。
现在开始有趣的部分了，相乘后他们可以用一个矩阵代表三个变换，假定有一个方法m3.multiply可以将两个矩阵相乘并返回结果。
为了方便讲解，我们先创建平移，旋转和缩放矩阵。


var m3 = {
  translation: function(tx, ty) {
    return [
      1, 0, 0,
      0, 1, 0,
      tx, ty, 1,
    ];
  },
  rotation: function(angleInRadians) {
    var c = Math.cos(angleInRadians);
    var s = Math.sin(angleInRadians);
    return [
      c,-s, 0,
      s, c, 0,
      0, 0, 1,
    ];
  },
  scaling: function(sx, sy) {
    return [
      sx, 0, 0,
      0, sy, 0,
      0, 0, 1,
    ];
  },
};
// 现在该修改着色器了，原来的着色器像这样
<script id="vertex-shader-2d" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
  // 缩放
  vec2 scaledPosition = a_position * u_scale;
  // 旋转
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);
  // 平移
  vec2 position = rotatedPosition + u_translation;
  ...
//  新着色器就简单多了。
<script id="vertex-shader-2d" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 u_matrix;
void main() {
  // 将位置乘以矩阵
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...
 // 使用方法
  // 绘制场景
  function drawScene() {
    ,,,
    // 计算矩阵
    var translationMatrix = m3.translation(translation[0], translation[1]);
    var rotationMatrix = m3.rotation(angleInRadians);
    var scaleMatrix = m3.scaling(scale[0], scale[1]);
    // 矩阵相乘
    var matrix = m3.multiply(translationMatrix, rotationMatrix);
    matrix = m3.multiply(matrix, scaleMatrix);
    // 设置矩阵
    gl.uniformMatrix3fv(matrixLocation, false, matrix);
    // 绘制图形
    gl.drawArrays(gl.TRIANGLES, 0, 18);
}

二 . 点在二维空间中点基本运动

<canvas id="canvas"></canvas>
<div id="uiContainer">
  <div id="ui">
    <div id="x"></div>
    <div id="y"></div>
    <div id="angle"></div>
    <div id="scaleX"></div>
    <div id="scaleY"></div>
  </div>
</div>
<!-- vertex shader -->
<script  id="vertex-shader-2d" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 u_matrix;
void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  // convert the position from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;
  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;
  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;
  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
}
</script>
<!-- fragment shader -->
<script  id="fragment-shader-2d" type="x-shader/x-fragment">
precision mediump float;
uniform vec4 u_color;
void main() {
   gl_FragColor = u_color;
}
</script>
<script src="https://webglfundamentals.org/webgl/resources/webgl-utils.js"></script>
<script src="https://webglfundamentals.org/webgl/resources/webgl-lessons-ui.js"></script>
"use strict";
function main() {
  // Get A WebGL context
  /** @type {HTMLCanvasElement} */
  var canvas = document.querySelector("#canvas");
  var gl = canvas.getContext("webgl");
  if (!gl) {
    return;
  }
  // setup GLSL program
  var program = webglUtils.createProgramFromScripts(gl, ["vertex-shader-2d", "fragment-shader-2d"]);
  // look up where the vertex data needs to go.
  var positionLocation = gl.getAttribLocation(program, "a_position");
  // lookup uniforms
  var resolutionLocation = gl.getUniformLocation(program, "u_resolution");
  var colorLocation = gl.getUniformLocation(program, "u_color");
  var matrixLocation = gl.getUniformLocation(program, "u_matrix");
  // Create a buffer to put positions in
  var positionBuffer = gl.createBuffer();
  // Bind it to ARRAY_BUFFER (think of it as ARRAY_BUFFER = positionBuffer)
  gl.bindBuffer(gl.ARRAY_BUFFER, positionBuffer);
  // Put geometry data into buffer
  setGeometry(gl);
  var translation = [100, 150];
  var angleInRadians = 0;
  var scale = [1, 1];
  var color = [Math.random(), Math.random(), Math.random(), 1];
  drawScene();
  // Setup a ui.
  webglLessonsUI.setupSlider("#x", {value: translation[0], slide: updatePosition(0), max: gl.canvas.width });
  webglLessonsUI.setupSlider("#y", {value: translation[1], slide: updatePosition(1), max: gl.canvas.height});
  webglLessonsUI.setupSlider("#angle", {slide: updateAngle, max: 360});
  webglLessonsUI.setupSlider("#scaleX", {value: scale[0], slide: updateScale(0), min: -5, max: 5, step: 0.01, precision: 2});
  webglLessonsUI.setupSlider("#scaleY", {value: scale[1], slide: updateScale(1), min: -5, max: 5, step: 0.01, precision: 2});
  function updatePosition(index) {
    return function(event, ui) {
      translation[index] = ui.value;
      drawScene();
    };
  }
  function updateAngle(event, ui) {
    var angleInDegrees = 360 - ui.value;
    angleInRadians = angleInDegrees * Math.PI / 180;
    drawScene();
  }
  function updateScale(index) {
    return function(event, ui) {
      scale[index] = ui.value;
      drawScene();
    };
  }
  // Draw the scene.
  function drawScene() {
    webglUtils.resizeCanvasToDisplaySize(gl.canvas);
    // Tell WebGL how to convert from clip space to pixels
    gl.viewport(0, 0, gl.canvas.width, gl.canvas.height);
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Tell it to use our program (pair of shaders)
    gl.useProgram(program);
    // Turn on the attribute
    gl.enableVertexAttribArray(positionLocation);
    // Bind the position buffer.
    gl.bindBuffer(gl.ARRAY_BUFFER, positionBuffer);
    // Tell the attribute how to get data out of positionBuffer (ARRAY_BUFFER)
    var size = 2;          // 2 components per iteration
    var type = gl.FLOAT;   // the data is 32bit floats
    var normalize = false; // don't normalize the data
    var stride = 0;        // 0 = move forward size * sizeof(type) each iteration to get the next position
    var offset = 0;        // start at the beginning of the buffer
    gl.vertexAttribPointer(
        positionLocation, size, type, normalize, stride, offset);
    // set the resolution
    gl.uniform2f(resolutionLocation, gl.canvas.width, gl.canvas.height);
    // set the color
    gl.uniform4fv(colorLocation, color);
    // Compute the matrices
    var translationMatrix = m3.translation(translation[0], translation[1]);
    var rotationMatrix = m3.rotation(angleInRadians);
    var scaleMatrix = m3.scaling(scale[0], scale[1]);
    // Multiply the matrices.
    var matrix = m3.multiply(scaleMatrix, rotationMatrix);
    matrix = m3.multiply(matrix, translationMatrix);
    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);
    // Draw the geometry.
    var primitiveType = gl.TRIANGLES;
    var offset = 0;
    var count = 18;  // 6 triangles in the 'F', 3 points per triangle
    gl.drawArrays(primitiveType, offset, count);
  }
}
var m3 = {
  translation: function(tx, ty) {
    return [
      1, 0, 0,
      0, 1, 0,
      tx, ty, 1,
    ];
  },
  rotation: function(angleInRadians) {
    var c = Math.cos(angleInRadians);
    var s = Math.sin(angleInRadians);
    return [
      c,-s, 0,
      s, c, 0,
      0, 0, 1,
    ];
  },
  scaling: function(sx, sy) {
    return [
      sx, 0, 0,
      0, sy, 0,
      0, 0, 1,
    ];
  },
  multiply: function(a, b) {
    var a00 = a[0 * 3 + 0];
    var a01 = a[0 * 3 + 1];
    var a02 = a[0 * 3 + 2];
    var a10 = a[1 * 3 + 0];
    var a11 = a[1 * 3 + 1];
    var a12 = a[1 * 3 + 2];
    var a20 = a[2 * 3 + 0];
    var a21 = a[2 * 3 + 1];
    var a22 = a[2 * 3 + 2];
    var b00 = b[0 * 3 + 0];
    var b01 = b[0 * 3 + 1];
    var b02 = b[0 * 3 + 2];
    var b10 = b[1 * 3 + 0];
    var b11 = b[1 * 3 + 1];
    var b12 = b[1 * 3 + 2];
    var b20 = b[2 * 3 + 0];
    var b21 = b[2 * 3 + 1];
    var b22 = b[2 * 3 + 2];
    return [
      b00 * a00 + b01 * a10 + b02 * a20,
      b00 * a01 + b01 * a11 + b02 * a21,
      b00 * a02 + b01 * a12 + b02 * a22,
      b10 * a00 + b11 * a10 + b12 * a20,
      b10 * a01 + b11 * a11 + b12 * a21,
      b10 * a02 + b11 * a12 + b12 * a22,
      b20 * a00 + b21 * a10 + b22 * a20,
      b20 * a01 + b21 * a11 + b22 * a21,
      b20 * a02 + b21 * a12 + b22 * a22,
    ];
  },
};
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,
          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,
          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90,
      ]),
      gl.STATIC_DRAW);
}
main();

三. 再一步转化

逐步观察，首先，“从像素坐标转换到 0.0 到 1.0”，事实上是一个缩放变换，第二步也是缩放变换，接着是一个平移和一个 Y 为 -1 的缩放。我们可以将这些操作放入一个矩阵传给着色器，创建两个缩放矩阵，一个缩放 1.0/分辨率，另一个缩放 2.0 ，第三个平移 -1.0,-1.0 然后第四个将 Y 缩放 -1。然后将他们乘在一起，由于运算很简单，所以我们就直接定义一个 projection 方法，根据分辨率直接生成矩阵。


var m3 = {
  projection: function(width, height) {
    // 注意：这个矩阵翻转了 Y 轴，所以 0 在上方
    return [
      2 / width, 0, 0,
      0, -2 / height, 0,
      -1, 1, 1
    ];
  },
  // 矩阵部分的代码可以进一步修改
    // 绘制场景
  function drawScene() {
    ...
    // 计算矩阵
    var projectionMatrix = m3.projection(
        gl.canvas.clientWidth, gl.canvas.clientHeight);
    ...
    // 矩阵相乘
    var matrix = m3.multiply(projectionMatrix, translationMatrix);
    matrix = m3.multiply(matrix, rotationMatrix);
    matrix = m3.multiply(matrix, scaleMatrix);
    ...
  }
<script id="vertex-shader-2d" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform mat3 u_matrix;
void main() {
  // 使位置和矩阵相乘
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

终极公式：gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1)